
摘要: 针对车辆主动悬架的免模型振动控制问题,提出了结合饱和超螺旋算法的实际输出反馈控制策略。在控制 设计中,考虑测量噪声和未知动态的影响,采用高阶滑模观测器估计系统的集中不确定性以及状态变量。为了保 证二阶滑模有限时间可达、且控制信号连续,采用一个新的饱和超螺旋算法设计系统控制器。该方法无需精确的 反馈线性化,仅需测量一个状态变量,减小了控制实施成本及复杂性。通过调节控制增益可保证系统状态的渐近 稳定性和有界性。通过硬件回路实验验证了控制策略的有效性,仿真和实验结果表明,该方法相对于传统的比例 积分( PD) 及线性二次调节器( LQR) 控制具有更好的减振效果,控制输出抖振较小。频响结果显示,被动控制的加 速度增益峰值为 44. 7 dB,LQR 控制的加速度增益峰值为29. 4 dB,而所提控制方法的加速度增益峰值仅为13. 5 dB,舒 适性得到较大的改善。
关键词: 车辆; 主动悬架; 二阶滑模; 输出反馈控制; 滑模观测器
1 两自由度车辆主动悬架模型 两自由度车辆主动悬架模型如图 1 所示。图 中,主动悬架部分包含弹簧和阻尼器,以及一个伺服 电机执行器。将轮胎部分简化为一个弹性元件和阻 尼元件。在实际的输出反馈控制中,悬架动态及轮胎动态难以精确测量,故无法实现精确的反馈补偿,需应 用状态观测器对部分状态及动态进行估计。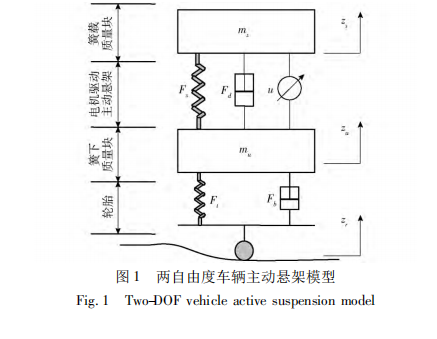 根据牛顿第二定律可得系统的振动方程为
根据牛顿第二定律可得系统的振动方程为
 由于 ρ 包含弹性力和阻尼力、控制误差和摄动 动态,且在输出反馈控制中,仅能测量一个状态量, 故精确的反馈线性化难以实施。
根据以往的研究可 知,主动悬架系统是有界输入、有界状态稳定系统, 故可将 ρ 定义为一个总的不确定项,并假设 ρ 是全 局有界且 Lipschitz 连续的函数,即 | ρ· | ≤L,L > 0 可 以通过实验测定。
由于 ρ 包含弹性力和阻尼力、控制误差和摄动 动态,且在输出反馈控制中,仅能测量一个状态量, 故精确的反馈线性化难以实施。
根据以往的研究可 知,主动悬架系统是有界输入、有界状态稳定系统, 故可将 ρ 定义为一个总的不确定项,并假设 ρ 是全 局有界且 Lipschitz 连续的函数,即 | ρ· | ≤L,L > 0 可 以通过实验测定。

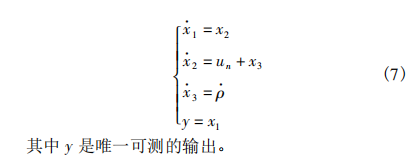 在控制目标中,选择 y 为被控量,除了需要减小 簧载质量的垂直振动位移和加速度外,还需要保证 悬架动行程 zs - zu 处于安全的范围,即 | zs - zu | ≤ zmax,其中 zmax表示最大的极限值。考虑到轮胎的接 地性能与轮胎动行程呈正比,故尽量减小轮胎动行 程| zu - zr |,其中 zr 表示路面垂直位移。考虑控制饱 和,电机主动控制力须小于规定的极限值,设 umax为 最大的输出力,则| u |≤umax。
因此,控制目标为:
①在仅测量 y 且无测量噪声 情况下,保证系统的状态 x1 和 x2 渐近收敛到零,并 且二阶滑模可达。
②在仅测量 y 但存在测量噪声情 况下,保证系统的状态 x1 渐近收敛到任意小的邻 域,并且二阶滑模可达。
③保证悬架动行程和控制 力在规定的范围内,同时尽可能减小轮胎动行程。
在控制目标中,选择 y 为被控量,除了需要减小 簧载质量的垂直振动位移和加速度外,还需要保证 悬架动行程 zs - zu 处于安全的范围,即 | zs - zu | ≤ zmax,其中 zmax表示最大的极限值。考虑到轮胎的接 地性能与轮胎动行程呈正比,故尽量减小轮胎动行 程| zu - zr |,其中 zr 表示路面垂直位移。考虑控制饱 和,电机主动控制力须小于规定的极限值,设 umax为 最大的输出力,则| u |≤umax。
因此,控制目标为:
①在仅测量 y 且无测量噪声 情况下,保证系统的状态 x1 和 x2 渐近收敛到零,并 且二阶滑模可达。
②在仅测量 y 但存在测量噪声情 况下,保证系统的状态 x1 渐近收敛到任意小的邻 域,并且二阶滑模可达。
③保证悬架动行程和控制 力在规定的范围内,同时尽可能减小轮胎动行程。
 2 高阶滑模观测器设计
设计一个高阶滑模观测器估计系统的状态 x2 以及总的不确定量 ρ。考虑系统( 7) ,引入观测器
2 高阶滑模观测器设计
设计一个高阶滑模观测器估计系统的状态 x2 以及总的不确定量 ρ。考虑系统( 7) ,引入观测器
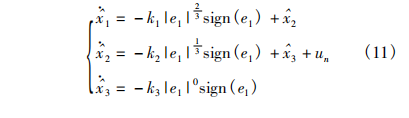
 3 基于观测器的饱和超螺旋算法设计
在控制算法设计中,不依赖集中不确定量 ρ 的 观测误差,仅需要状态量 x1。即存在噪声时,系统 状态也二阶滑模可达。
3 基于观测器的饱和超螺旋算法设计
在控制算法设计中,不依赖集中不确定量 ρ 的 观测误差,仅需要状态量 x1。即存在噪声时,系统 状态也二阶滑模可达。
 注意到设计的控制律 uc 和 us 都不需总的不确定量 ρ 的精确补偿,因此,具有很好的实用性和鲁棒性。定义 a( t) = - c1 e2,针对 a( t) 分两种情况进行 讨论。
( 1) 当无测量噪声时,根据定理 1,e2 将在有限 时间 T1 内收敛到零,故 a( t) = 0,t > T1。设计饱和超螺旋控制律。
注意到设计的控制律 uc 和 us 都不需总的不确定量 ρ 的精确补偿,因此,具有很好的实用性和鲁棒性。定义 a( t) = - c1 e2,针对 a( t) 分两种情况进行 讨论。
( 1) 当无测量噪声时,根据定理 1,e2 将在有限 时间 T1 内收敛到零,故 a( t) = 0,t > T1。设计饱和超螺旋控制律。

 在无测量噪声情况下,无需整定控制律( 18) 的 控制增益,仅需满足式( 19) 约束控制输出即可,提 供了较大的便利。(
2) 当有测量噪声时,假设噪声的量级为 δ,即 | ) x1 - x1 |≤δ,则在有限时间 T1 内 | e2 | ≤μL1 /2 δ1 /2,其 中 μ≥1,) x1 表示含测量噪声的测试信号。假设a( t) 全局有界并且是 Lipschitz 连续的,即 | a( t) | ≤aM, | a·( t) |≤La。
在无测量噪声情况下,无需整定控制律( 18) 的 控制增益,仅需满足式( 19) 约束控制输出即可,提 供了较大的便利。(
2) 当有测量噪声时,假设噪声的量级为 δ,即 | ) x1 - x1 |≤δ,则在有限时间 T1 内 | e2 | ≤μL1 /2 δ1 /2,其 中 μ≥1,) x1 表示含测量噪声的测试信号。假设a( t) 全局有界并且是 Lipschitz 连续的,即 | a( t) | ≤aM, | a·( t) |≤La。


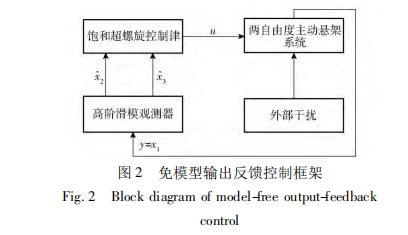
 因此,被控状态 x1 将渐近收敛到邻域| x1 | ≤Ω。Ω 的大小依赖于噪声级别以及系统的控制参数,通 过增大滑模增益 c1 可以任意地减小 Ω,故 x1 将收敛 到任意小的范围。闭环系统的控制框图见图 2,从图 2 可看出,控 制方法是简易且容易实施的,该控制方案仅需要测 量一个状态量,减少了实施成本,且不需模型的精确 参数,具有很强的鲁棒性和较高的收敛精度。
定理2: 考虑系统( 7) ,设计高阶滑模观测器( 11) 以及饱和超螺旋控制律( 23) ,若选择合适观测器增 益 ki 和控制器增益 κi 以及 c1、,则系统在滑模面 上二阶滑模可达,且有测量噪声时,状态 x1 能收敛 到任意小的界 Ω。
因此,被控状态 x1 将渐近收敛到邻域| x1 | ≤Ω。Ω 的大小依赖于噪声级别以及系统的控制参数,通 过增大滑模增益 c1 可以任意地减小 Ω,故 x1 将收敛 到任意小的范围。闭环系统的控制框图见图 2,从图 2 可看出,控 制方法是简易且容易实施的,该控制方案仅需要测 量一个状态量,减少了实施成本,且不需模型的精确 参数,具有很强的鲁棒性和较高的收敛精度。
定理2: 考虑系统( 7) ,设计高阶滑模观测器( 11) 以及饱和超螺旋控制律( 23) ,若选择合适观测器增 益 ki 和控制器增益 κi 以及 c1、,则系统在滑模面 上二阶滑模可达,且有测量噪声时,状态 x1 能收敛 到任意小的界 Ω。
 4 数值仿真
在 Matlab / Simulink 模块搭建闭环系统的仿真 模型。为了便于频域分析,假设悬架系统线性动态为
4 数值仿真
在 Matlab / Simulink 模块搭建闭环系统的仿真 模型。为了便于频域分析,假设悬架系统线性动态为

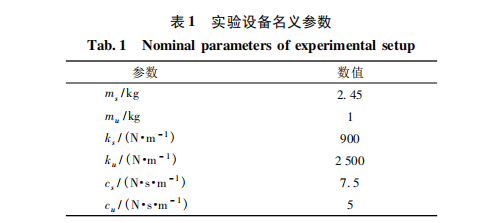 为了 便 于 描 述,定义本文所提出的方法为 HOSMO-SSTA。通过计算可得簧载质量的一阶固有 频率为 ωs = ks 槡 /ms = 19 rad / s,考虑到簧载质量的 固有频率接近 3 Hz,故首先采用频率为 3 Hz、幅值为 2 mm 的正弦波进行仿真道路测试。
路面波形为 zr = 0. 002sin( 6πt) m ( 31) 为了保证悬架系统的安全,根据系统的配置及 尺寸,最大悬架动行程取 2 cm,最大轮胎动行程为 2 cm,最大控制力为 10 N。正弦激励下位移和加速 度仿真结果如图 3、4 所示。
在共振频率激励下,被 动悬架的车身加速度峰值为 2. 78 m / s2,LQR 控制下 的车身加速度峰值为 0. 69 m / s2,HOSMO-SSTA 的车 身加速度峰值为 0. 20 m / s2,舒适性得到改善。
为了 便 于 描 述,定义本文所提出的方法为 HOSMO-SSTA。通过计算可得簧载质量的一阶固有 频率为 ωs = ks 槡 /ms = 19 rad / s,考虑到簧载质量的 固有频率接近 3 Hz,故首先采用频率为 3 Hz、幅值为 2 mm 的正弦波进行仿真道路测试。
路面波形为 zr = 0. 002sin( 6πt) m ( 31) 为了保证悬架系统的安全,根据系统的配置及 尺寸,最大悬架动行程取 2 cm,最大轮胎动行程为 2 cm,最大控制力为 10 N。正弦激励下位移和加速 度仿真结果如图 3、4 所示。
在共振频率激励下,被 动悬架的车身加速度峰值为 2. 78 m / s2,LQR 控制下 的车身加速度峰值为 0. 69 m / s2,HOSMO-SSTA 的车 身加速度峰值为 0. 20 m / s2,舒适性得到改善。
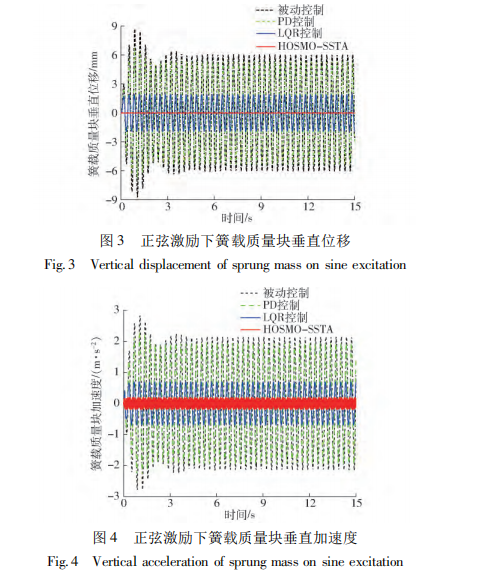 通过滤波成形法[10]生成幅值为 2 mm 的不规则 干扰对控制系统进行随机道路测试。图 5、6 分别为随机激励下的位移和加速度响应曲线,从图中可看 出,文中所提出的免模型控制方法具有最小的响应 幅值。
通过滤波成形法[10]生成幅值为 2 mm 的不规则 干扰对控制系统进行随机道路测试。图 5、6 分别为随机激励下的位移和加速度响应曲线,从图中可看 出,文中所提出的免模型控制方法具有最小的响应 幅值。
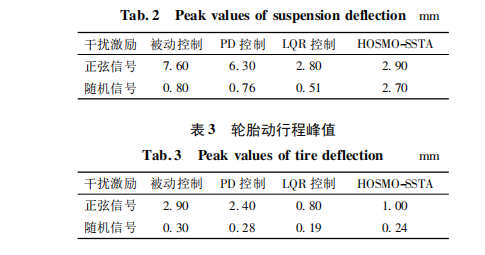
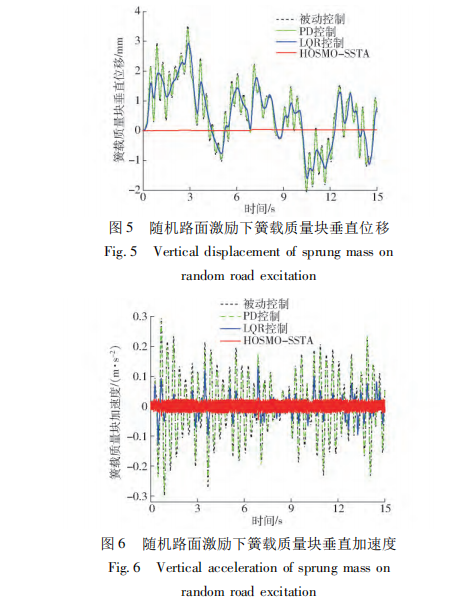 PD 控制、LQR 控制和 HOSMO-SSTA 控制的 加速度峰值分别为 0. 28、0. 13、0. 05 m / s2。不同路 面激励下的悬架动行程和轮胎动行程峰值如表 2、3 所示,所提出的控制方法具有较小的轮胎动行程,且 悬架动行程小于最大极限值 2 cm。
PD 控制、LQR 控制和 HOSMO-SSTA 控制的 加速度峰值分别为 0. 28、0. 13、0. 05 m / s2。不同路 面激励下的悬架动行程和轮胎动行程峰值如表 2、3 所示,所提出的控制方法具有较小的轮胎动行程,且 悬架动行程小于最大极限值 2 cm。
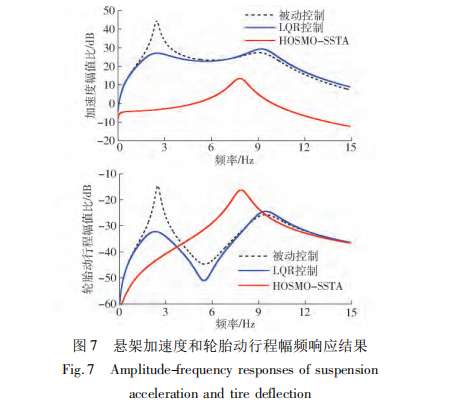
 为了便于频域分析,假设系统已经达到了二阶 滑模稳定点 ^s = ν = 0,根据悬架系统的零动态特性, 仿真得出图 7 所示加速度和轮胎动行程幅频响应。
被动控制的加速度增益峰值为 44. 7 dB,LQR 控制 下的加速度增益峰值为 29. 4 dB,而所提控制方法的加速度增益峰值仅为 13. 5 dB。
从图 7 可看出,在共 振频率3 Hz 附近,基于 HOSMO-SSTA 控制的加速度 小于被动和 LQR 的控制情况。HOSMO-SSTA 控制 的轮胎动行程增益峰值( - 16. 3 dB) 也小于被动控 制的增益峰值( - 14. 5 dB) ,在小于 4 Hz 及大于 9 Hz 的范围内接地性能改善效果较为明显。
为了便于频域分析,假设系统已经达到了二阶 滑模稳定点 ^s = ν = 0,根据悬架系统的零动态特性, 仿真得出图 7 所示加速度和轮胎动行程幅频响应。
被动控制的加速度增益峰值为 44. 7 dB,LQR 控制 下的加速度增益峰值为 29. 4 dB,而所提控制方法的加速度增益峰值仅为 13. 5 dB。
从图 7 可看出,在共 振频率3 Hz 附近,基于 HOSMO-SSTA 控制的加速度 小于被动和 LQR 的控制情况。HOSMO-SSTA 控制 的轮胎动行程增益峰值( - 16. 3 dB) 也小于被动控 制的增益峰值( - 14. 5 dB) ,在小于 4 Hz 及大于 9 Hz 的范围内接地性能改善效果较为明显。
 5 实验
为了进一步验证所提控制器的性能,搭建主动 悬架系统实验台如图 8 所示。
实验中,采用 C 语言 进行编译控制器程序,内嵌一个 TLC 程序进行硬件 加速,最大采样频率设为 1 000 Hz,噪声级别 δ 为 5 × 10 - 6。实验中,通过一个 10 bit 的编码器测量各 部分位移,加速度计安装在簧载质量块上,用于测量 垂直加速度。路面激励由底部的伺服电机产生。
5 实验
为了进一步验证所提控制器的性能,搭建主动 悬架系统实验台如图 8 所示。
实验中,采用 C 语言 进行编译控制器程序,内嵌一个 TLC 程序进行硬件 加速,最大采样频率设为 1 000 Hz,噪声级别 δ 为 5 × 10 - 6。实验中,通过一个 10 bit 的编码器测量各 部分位移,加速度计安装在簧载质量块上,用于测量 垂直加速度。路面激励由底部的伺服电机产生。
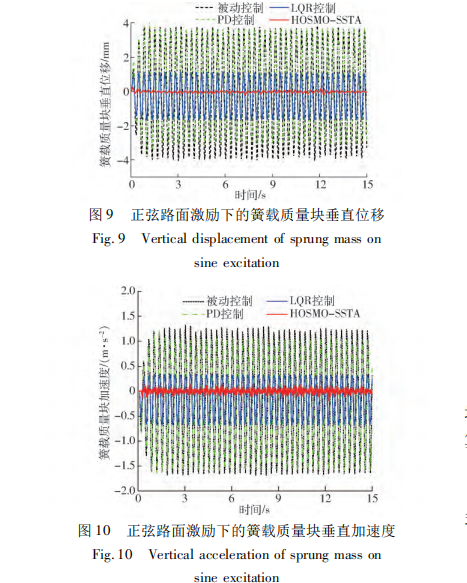
 首先采用式( 31) 所示的正弦路面激励进行测 试,测试结果见图 9 ~ 13。在主动悬架的性能评估 中,车身加速度的均方根与舒适性密切相关,从 图 9、10 可看出,HOSMO-SSTA 方法明显优于传统的 PD 控制及 LQR 控制。本文方法也优于基于线性拓张观测器的反演控制[9]。
在设计中,不需要精确的 反馈线性化,考虑实际的测量噪声,仅通过整定控制。
首先采用式( 31) 所示的正弦路面激励进行测 试,测试结果见图 9 ~ 13。在主动悬架的性能评估 中,车身加速度的均方根与舒适性密切相关,从 图 9、10 可看出,HOSMO-SSTA 方法明显优于传统的 PD 控制及 LQR 控制。本文方法也优于基于线性拓张观测器的反演控制[9]。
在设计中,不需要精确的 反馈线性化,考虑实际的测量噪声,仅通过整定控制。
 增益 c1 即可调节 x1 的振动幅值。系统的均方根计 算式为
增益 c1 即可调节 x1 的振动幅值。系统的均方根计 算式为
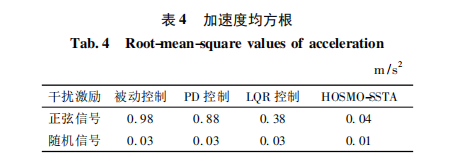
 表 4 给出了正弦激励下加速度均方根对比,从 表 4 可看出,HOSMO-SSTA 控制下的加速度均方根 比其他方法低一个数量级,且相应的 Pobj为 95% ,从 而验证了该方法具有更好的主动减振性能。
表 4 给出了正弦激励下加速度均方根对比,从 表 4 可看出,HOSMO-SSTA 控制下的加速度均方根 比其他方法低一个数量级,且相应的 Pobj为 95% ,从 而验证了该方法具有更好的主动减振性能。
 控制过程中,为了减小控制幅值,取 = 3 N。另一方面,为了减小控制抖振并保证收敛精度,不需 要用饱和函数替代符号函数,仅需保证控制器的增 益不宜过大即可。
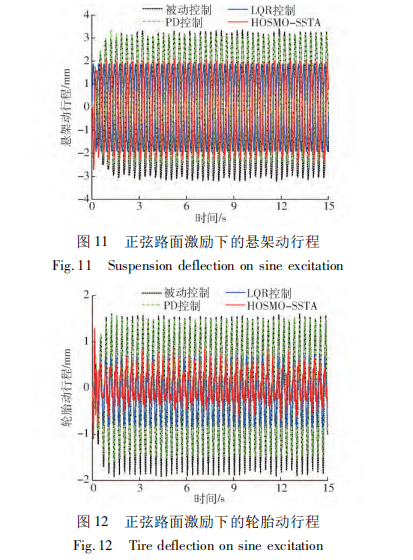
当抖振频率大于电机的执行速率 时,容易造成过大的控制误差。由图 11、12 可知,闭 环系统的悬架动行程也小于被动控制及 PD 控制, 虽然略大于 LQR 控制的情况,但总体满足设计要 求。
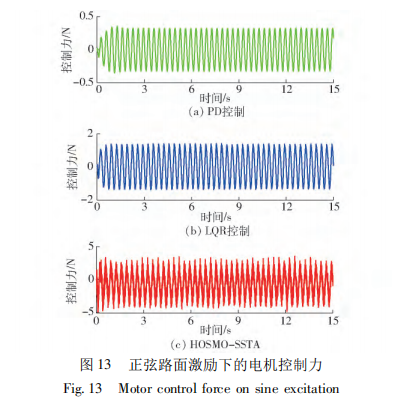
同时,轮胎动行程达到最小,故 HOSMO-SSTA控制下的主动悬架具有更好的接地性能。从图 13 可看出,相对于传统的一阶滑模控制,本文所提的方 法本身具有较小的抖振,符合二阶滑模算法的属性。在传统的一阶滑模控制中,为了减小抖振,通常用饱 和函数替代符号函数,降低了系统的收敛精度。
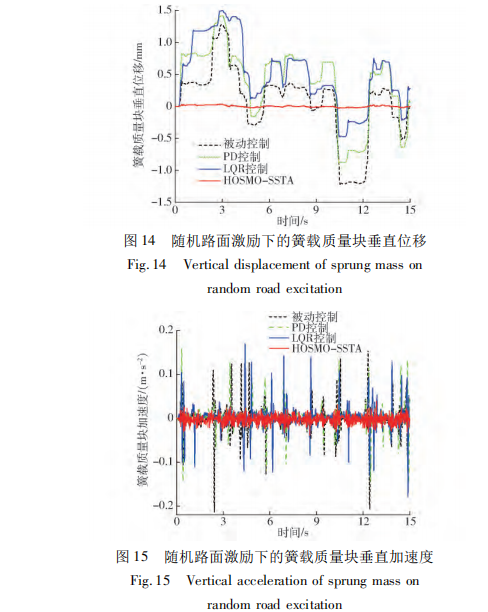
图 14、15 为随机路面激励下的簧载质量块的振 动波形图,从图可知,在不规则干扰下,文中所提方 法具有很好的减振效果,明显优于传统的被动控制、 PD 控制及 LQR 控制。结合表 4 和式( 33) ,可计算 出相对于其他 3 种方法,HOSMO-SSTA 控制下的加 速度均方根下降了 70% 以上,而 PD 控制及 LQR 控 制对不规则干扰的抑制能力较弱。
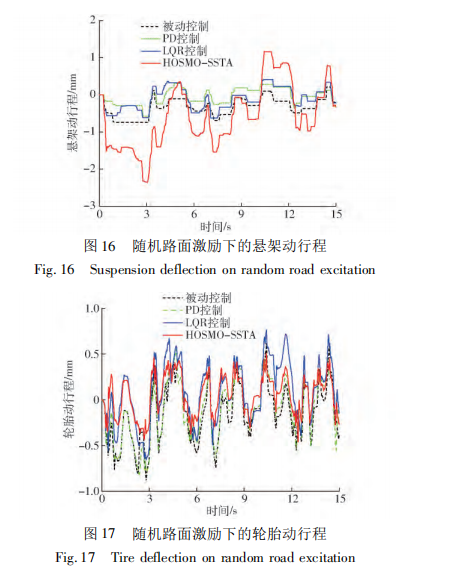
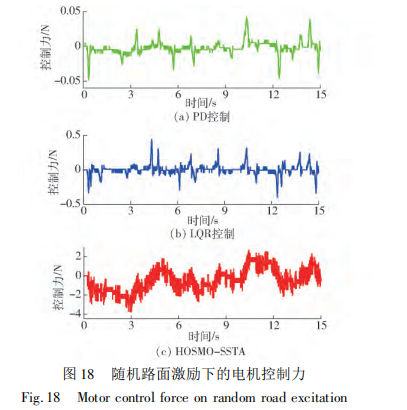
图 16、17 为悬架 动行程及轮胎动行程响应波形,所有方法均在安全 的行程范围内。图 18 给出了电机控制力的波形图, 虽然具有一定的抖振,但在采样控制下,仍然小于一 阶滑模的情况。
控制过程中,为了减小控制幅值,取 = 3 N。另一方面,为了减小控制抖振并保证收敛精度,不需 要用饱和函数替代符号函数,仅需保证控制器的增 益不宜过大即可。
当抖振频率大于电机的执行速率 时,容易造成过大的控制误差。由图 11、12 可知,闭 环系统的悬架动行程也小于被动控制及 PD 控制, 虽然略大于 LQR 控制的情况,但总体满足设计要 求。
同时,轮胎动行程达到最小,故 HOSMO-SSTA控制下的主动悬架具有更好的接地性能。从图 13 可看出,相对于传统的一阶滑模控制,本文所提的方 法本身具有较小的抖振,符合二阶滑模算法的属性。在传统的一阶滑模控制中,为了减小抖振,通常用饱 和函数替代符号函数,降低了系统的收敛精度。
图 14、15 为随机路面激励下的簧载质量块的振 动波形图,从图可知,在不规则干扰下,文中所提方 法具有很好的减振效果,明显优于传统的被动控制、 PD 控制及 LQR 控制。结合表 4 和式( 33) ,可计算 出相对于其他 3 种方法,HOSMO-SSTA 控制下的加 速度均方根下降了 70% 以上,而 PD 控制及 LQR 控 制对不规则干扰的抑制能力较弱。
图 16、17 为悬架 动行程及轮胎动行程响应波形,所有方法均在安全 的行程范围内。图 18 给出了电机控制力的波形图, 虽然具有一定的抖振,但在采样控制下,仍然小于一 阶滑模的情况。
 在无模型精确参数和动态的情况下,HOSMOSSTA 控制的主动悬架系统具有良好的主动减振性 能。在簧载质量块的一阶共振频率附近,具有较好 的抗干扰和悬架综合性能。
同时,接地性能也得到 改善。由于实际的系统存在一定的未建模非线性动 态、参数摄动以及电机作动器的执行误差,导致实验和仿真结果略有差别,但减振效果能够较好地吻合 及匹配。由于所提方法不依赖模型的参数及形式, 可以应用于其他类型的主动悬架系统,具有较强的 实用性。
在无模型精确参数和动态的情况下,HOSMOSSTA 控制的主动悬架系统具有良好的主动减振性 能。在簧载质量块的一阶共振频率附近,具有较好 的抗干扰和悬架综合性能。
同时,接地性能也得到 改善。由于实际的系统存在一定的未建模非线性动 态、参数摄动以及电机作动器的执行误差,导致实验和仿真结果略有差别,但减振效果能够较好地吻合 及匹配。由于所提方法不依赖模型的参数及形式, 可以应用于其他类型的主动悬架系统,具有较强的 实用性。
 6 结束语
针对电机驱动的两自由度车辆主动悬架系统的 免模型实际输出反馈控制问题,提出了基于高阶滑模观测器的饱和超螺旋控制策略。控制方法简易 有效,仅需测量一个状态量,且不需要精确的模型 参数,具有较好的实用性和鲁棒性。
通过调整控 制参数,能够约束控制律的输出幅值。仿真与实 验结果表明了控制策略的有效性,在两种典型的 路面干扰工况下,提出的 HOSMO-SSTA 方法具有更好的悬架综合性能,舒适性及接地性能优于传 统的被动控制、PD 控制及 LQR 控制方法。
频域结果显示,被动控制的加速度增益峰值为 44. 7 dB, LQR 控制的加速度增益峰值为 29. 4 dB,而所提控 制方法的加速度增益峰值仅为 13. 5 dB,舒适性得 到较大改善。
文章来源:农 业 机 械 学 报
作者:王 刚 周知进 陈海虹
6 结束语
针对电机驱动的两自由度车辆主动悬架系统的 免模型实际输出反馈控制问题,提出了基于高阶滑模观测器的饱和超螺旋控制策略。控制方法简易 有效,仅需测量一个状态量,且不需要精确的模型 参数,具有较好的实用性和鲁棒性。
通过调整控 制参数,能够约束控制律的输出幅值。仿真与实 验结果表明了控制策略的有效性,在两种典型的 路面干扰工况下,提出的 HOSMO-SSTA 方法具有更好的悬架综合性能,舒适性及接地性能优于传 统的被动控制、PD 控制及 LQR 控制方法。
频域结果显示,被动控制的加速度增益峰值为 44. 7 dB, LQR 控制的加速度增益峰值为 29. 4 dB,而所提控 制方法的加速度增益峰值仅为 13. 5 dB,舒适性得 到较大改善。
文章来源:农 业 机 械 学 报
作者:王 刚 周知进 陈海虹








 本文提出了一种结合饱和超螺旋算法的实际输出反馈控制策略,用于解决车辆主动悬架的振动控制问题。在考虑测量噪声和未知动态的情况下,通过高阶滑模观测器来估计系统不确定性及状态变量。控制设计确保了二阶滑模的有限时间可达和控制信号连续性,降低了实施成本和复杂性。实验验证显示,该策略相对于传统PD和LQR控制具有更好的减振效果,提高了舒适性。
本文提出了一种结合饱和超螺旋算法的实际输出反馈控制策略,用于解决车辆主动悬架的振动控制问题。在考虑测量噪声和未知动态的情况下,通过高阶滑模观测器来估计系统不确定性及状态变量。控制设计确保了二阶滑模的有限时间可达和控制信号连续性,降低了实施成本和复杂性。实验验证显示,该策略相对于传统PD和LQR控制具有更好的减振效果,提高了舒适性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








