2022南京中考家长交流群QQ群:724824123
【学习目标】
1.了解不等式的意义,认识不等式和等式都可以用来刻画现实世界中的数量关系。
2. 知道不等式解集的概念并会在数轴上表示解集。
3. 理解不等式的三条基本性质,并会简单应用。
【要点梳理】
知识点一、不等式的概念
一般地,用“<”、 “>”、“≤”或“≥”表示大小关系的式子,叫做不等式.用“≠”表示不等关系的式子也是不等式。
要点诠释:
(1)不等号“<”或“>”表示不等关系,它们具有方向性,不等号的开口所对的数较大。
(2)五种不等号的读法及其意义:
符号 | 读法 | 意义 |
“≠” | 读作“不等于” | 它说明两个量之间的关系是不相等的,但不能确定哪个大,哪个小 |
“<” | 读作“小于” | 表示左边的量比右边的量小 |
“>” | 读作“大于” | 表示左边的量比右边的量大 |
“≤” | 读作“小于或等于” | 即“不大于”,表示左边的量不大于右边的量 |
“≥” | 读作“大于或等于” | 即“不小于”,表示左边的量不小于右边的量 |
(2)五种不等号的读法及其意义:
(3)有些不等式中不含未知数,如3<4,-1>-2;有些不等式中含有未知数,如2x>5中,x表示未知数,对于含有未知数的不等式,当未知数取某些值时,不等式的左、右两边符合不等号所表示的大小关系,我们说不等式成立,否则,不等式不成立。
知识点二、不等式的解及解集
1.不等式的解:
能使不等式成立的未知数的值,叫做不等式的解。
2.不等式的解集:
对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.
要点诠释:
不等式的解 | 是具体的未知数的值,不是一个范围 |
不等式的解集 | 是一个集合,是一个范围.其含义: ①解集中的每一个数值都能使不等式成立; ②能够使不等式成立的所有数值都在解集中 |
3.不等式的解集的表示方法
(1)用最简的不等式表示:一般地,一个含有未知数的不等式有无数个解,其解集是一个范围,这个范围可用最简单的不等式来表示.如:不等式x-2≤6的解集为x≤8.
(2)用数轴表示:不等式的解集可以在数轴上直观地表示出来,形象地表明不等式的无限个解.如图所示:
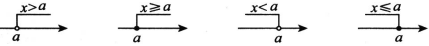
要点诠释:
借助数轴可以将不等式的解集直观地表示出来,在应用数轴表示不等式的解集时,要注意两个“确定”:一是确定“边界点”,若边界点是不等式的解,则用实心圆点,若边界点不是不等式的解,则用空心圆圈;二是确定方向,对边界点a而言,x>a或x≥a向右画;对边界点a而言,x<a或x≤a向左画.注意:在表示a的点上画空心圆圈,表示不包括这一点。
知识点三、不等式的基本性质
不等式的基本性质1:
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
用式子表示:如果a>b,那么a±c>b±c.
不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
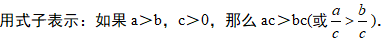
不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。
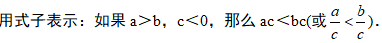
要点诠释:
不等式的基本性质的掌握应注意以下几点:
(1)不等式的基本性质是对不等式变形的重要依据,是学习不等式的基础,它与等式的两条性质既有联系,又有区别,注意总结、比较、体会.
(2)运用不等式的性质对不等式进行变形时,要特别注意性质2和性质3的区别,在乘(或除以)同一个数时,必须先弄清这个数是正数还是负数,如果是负数,不等号的方向要改变.
【典型例题】
类型一、不等式的概念
例1.有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、小砝码皆为1克,且下图是将糖果与砝码放在等臂天平上的两种情形。
判断下列正确的情形是 ( )
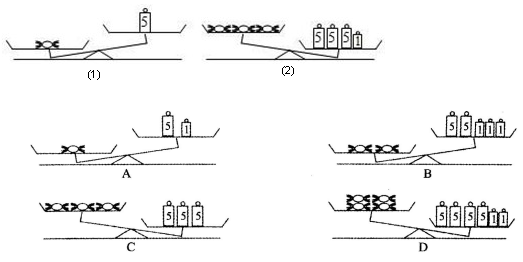
【思路点拨】
根据图示可知1个糖果的质量>5克,3个糖果的质量<16克,依此求出1个糖果的质量取值范围,再在4个选项中找出情形正确的。
【答案】D
【解析】
解:由图(1)知,每一个糖果的重量大于5克,由图(2)知:3个糖果的重量小于

【总结升华】
观察图示,确定大小.本题涉及的知识点是不等式,涉及的数学思想是数形结合思想,解决问题的基本思路是根据图示信息列出不等式。
类型二、不等式的解及解集
例2. 若关于x的不等式x≤a只有三个正整数解,求a的取值范围.
【思路点拨】
首先根据题意确定三个正整数解,然后再确定a的范围.
【答案】
3≤a<4
【解析】
解:∵不等式x≤a只有三个正整数解,
∴三个正整数解为:1,2,3,
∴3≤a<4,
【总结升华】
此题主要考查了一元一次不等式的整数解,做此题的关键是确定好三个正整数解。
例3. 如图所示,图中阴影部分表示x的取值范围,则下列表示中正确的是( )

A.-3≤x<2 B.-3<x≤2 C.-3≤x≤2 D.-3<x<2
【思路点拨】
x表示-3右边的数,即大于-3,并且是2以及2左边的数,即小于或等于2的数.
【答案】B
【解析】
解: A、因为-3≤x<2,在数轴上-3的点应该是实心的圆点;C、因为-3≤x≤2,在数轴上-3和2的点应该都是实心的圆点;D、因为-3<x<2,在数轴上-3和2的点应该都是空心的圆点;故选B。
【总结升华】
在数轴上 表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示,“>”,“≥”向右画;“<”,“≤”向左画。
举一反三:
【变式】根据如图所示的程序计算,若输入x的值为1,则输出y的值为____.

【答案】4
提示:由程序图可知,计算求值时所使用的数学表达式为y=2x²-4.把x=1输入求值,若求得的结果大于0,则直接得到输出值y;若求得的结果小于0,则需要把得到的结果作为输入值再代入计算,循环往复,直到使最终的结果大于0为止。
类型三、不等式的基本性质

【思路点拨】
观察方程组不难发现只要把两个方程相加即能求出x+y的值.因为x+y<2,故可以构建关于a的不等式.然后利用不等式的性质就能求出a的取值范围.
【答案】a<4
【解析】
解:将两方程相加得:4x+4y=4+a.

将不等式的两边同乘以4得4+a<8.
将不等式的两边同时减去4得a<4.
故a的取值范围是a<4.
【总结升华】
解关于x的一元一次不等式,就是要将不等式逐步化为x>a或x<a的形式,化简的依据是不等式的性质.
举一反三:
【变式1】

【答案】
a>1.
【解析】
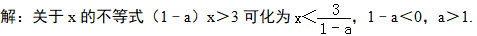
【变式2】a、b是有理数,下列各式中成立的是( ).
A.若a>b,则a²>b²;
B.若a²>b²,则a>b
C.若a≠b,则|a|≠|b|
D.若|a|≠|b|,则a≠b
【答案】
D



免责申明:本音频、视频和相关素材来源于网络。转载出于传递信息和学习之目的。如转载涉及版权等问题, 请立即联系管理员,我们会更改或删除相关文章,保证您的权利。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








