频数直方图的步骤_QC七大工具之直方图

直方图

质量的偏差是无法回避的，判断质量的偏差是否由于偶然原因引起的，有必要对质量偏差状况进行实际测量和采集数据。

以产品重量为例，从罗列的数据表是不能知道产品重量的偏差状态的。为了把握重量的偏差状态，有必要将其数据表换写成能读取偏差状态的频数表。

直方图是将数据存在的区域分成几个区间，各区间里分布的数据的出现次数做成频数表，以柱形的高度来表示各区间的所属次数，能够清楚地知道偏差的状态。

直方图NO.1直方图的作法

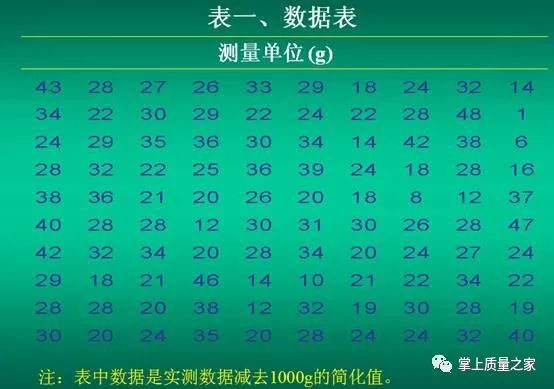
现以某厂生产的产品重量为例，对应用直方图的步骤加以说明：(1)收集数据。作直方图的数据一般应大于50个。本例在生产过程中收集了100个数据，列于表一中。(2)确定数据的极差(R)。用数据的最大值减去最小值求得。本例最大值Xmax=48(cg),最小值Xmin=1(cg),所以极差R=48-1=47(cg).

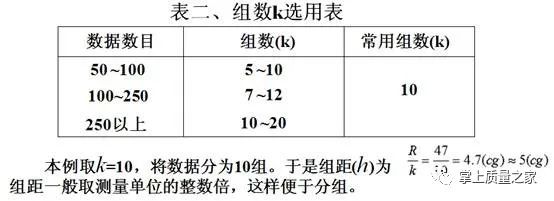
(3)确定组距(h)。先确定直方图的组数，然后以此组数去除极差，可得直方图每组的宽度，即组距。组数的确定要适当。组数太少，会引起较大计算误差；组数太多，会影响数据分组规律的明显性，且计算工作量加大。组数(k)的确定可参考组数(k)选用表二。

(4 )确定各组的界限值。为避免出现数据值与组界限值重合而造成频数据计算困难，组的界限值单位应取最小测量单位的1/2。本例最小测量单位是个位，其界限值应取0.5。分组时应把数据表中最大值和最小值包括在内。
第一组下限值为：1-0.5=0.5;
第一组上限值为：第一组下限值加组距，即0.5+5=5.5;
第二组下限值就是第一组的上限值，即5.5；
第二组上限值就是第二组的下限值加组距，即5.5+5=10.5；
第三组以后，依此类推定出各组的组界。(5)编制频数分布表。把多个组上下界限值分别填入频数分布表内，并把数据表中的各个数据列入相应的组，统计各组频数据(f )。
(6)按数据值比例画出横坐标。
(7)按频数值比例画纵坐标。以观测值数目或百分数表示。
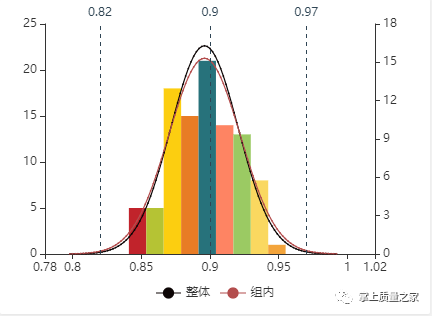
(8)画直方图。按纵坐标画出每个长方形的高度，它代表取落在此长方形中的数据数。(注意：每个长方形的宽度都是相等的。)在直方图上应标注出公差范围(T)、样本大小(n)、样本平均值(x)、样本标准偏差值(s)和x的位置等。

NO.2直方 图的几种分布形态剖析

分布形态	剖析
缺牙形的分布	每个一级其频数变得少些，如缺牙形、梳形牙。如此的形状是由于分级不当、测量器(千分尺、秤等)使用不当引起的，例如，对以每10g所分的级只能测量50g单位的秤测量时所引起的现象。另外，测量者的刻度读法的不当也会引起此类现象。
右畸变的分布	直方图的平均分布的中心的左侧，左侧的频数下降得很快，而右侧得频数下降得缓慢，左右不对称。理论上，由规格值等下限被受限，某值以下得数值不能得到时所引起的。 不纯物的成分在0%、不合格、缺陷在0附近时所出现的现象。分布的下摆拖长时，其理由在技术上是否能理解有必要研讨。
左畸变的分布	与上相反，由于理论值、规格值等上限受限时所引起的。例如：成品率、纯度接近100%时出现的现象。这时，如果去除左边的下摆，成品、纯度将会变得更好。另外，切断一定尺寸的物体时，如果切短了就不得不将其扔掉，所以常常会把它切长了，这种情况会引起此分布。
切边分布	直方图的平均值极端地靠近一侧，离分布的中心很远，相反的一侧其频数下降的很缓慢。将规格以下的制品全数去除时会引起此类现象。另外，测量的作假、测量误差、误检查时也会引起此现象，有必要就此检查一下。
二山形分布	分布的中心部分的频数较少，从而左右出现了两座山。平均值稍微有差异的几个分布相混时出现的现象。此时，有可能超出了规格值的一侧或者两侧。对所能考虑到的两台机器间、工种原料间是否有差异等原因进行分层，如果重新作直方图就能知道其不同点。
孤岛形分布	右端或左端有与其相分离的小岛。从不同的数据中有少量的数据混入时而出现的分布。要调查工序中有什么异常、测量是否有误、是否有其他工序的数据混入。如果管理严格，去除其孤岛，一般不良品会消失。

满足规格时的例子：

(1) 理想场合

直方图在规格的上限和下限之中，平均值也几乎在分布正当中。偏差在规格内稍微有些余裕，可以说是理想的。

(2) 两侧没有余裕的场合

偏差的范围正好与规格的上限和下限一致。因为没有什么余裕，所以不能令人安心。工序即使稍微有些变化，将有可能出现不合格品，所以要减少偏差。

(3) 余裕太多的场合

偏差的范围过分地满足规格的上限、下限，余裕太多。这时，可以改善规格，如为了严格控制偏差，花了不少时间精力的话，可以省略一部分工序使偏差稍微变大点。如果一边的规格余裕太多也可以采取同样的措施。

不满足规格时的例子：

(1) 平均值错位的场合

平均值朝某一方向错位，如技术上能简单地将平均值进行移动的话，只要平均值移到规格的中心上即可。

(2)平均值过分错位的场合

它是上面的极端的情况，偏差的范围并不坏，只是完全离开了规格的限界。

(3) 偏差非常大的场合

工序的偏差太大，这时称为工序能力不足。如果行的话，放宽规格。如果这还不能改变的话应对工序彻底改善或进行全数检查。

NO.3直方 图的使用方法

(1) 观察分布的形态来把握工序的异常点

如果工序有异常，其分布呈二山分布、切边分布等不规则分布。所以，通过对直方图的形态进行观察，就可以推测工序中发生了怎样的异常。

(2) 调查是否在规格之内

如果在规格之内的话，就能很清楚地把握住与分布之间的关系，能知道是偏向某一边的问题还是偏差的问题。具体计算平均值等就能推定其工序能力、不合格率。

(3) 偏向某一边、偏差原因的调查

画以机械、设备、材料、人方法和测量等分层的直方图，分析其不同点就可以知道偏向某一边、偏差的原因。但是，这时与特征因素图、帕累托图并用，从各个角度来进行分层是很重要的。

(4) 改善前后进行分层对改善效果进行调查

改善前和改善后级逆行能够进行分层，中心值的位置以及偏差的幅度是怎样变化的，对直方图进行比较的话就可以把握改善的效果。

NO.4正态分布的特点

(1) 曲线以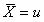对称轴，左右对称；

(2) 离u很近的，出现概率大；离u远的，出现概率小；

(3) σ决定分布曲线形状；

(4) 总体是1。

NO.5 如何衡量“产品群体的”质量？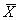

：衡量产品的群体的质量中心(即平均值)与规格的质量中心的吻合程度，最好是完全相等。

监控加工质量平均值(即质量中心变化)的变化工具。

S：定性的说，S值越小越好，表示群体质量对质量中心的离散程度，S小则离散度小。

监控产品质量离散程度，其实质是控制“加工精度”。