函数对称性常见公式_高中数学：还在为函数对称性周期性而烦恼，试试这种记忆方法...

请记住我们的口号：GoFine数学，重逻辑也重记忆！

今天我们给大家解决的是高中生普遍易混淆的函数对称性周期性表达式问题。

废话不多说，直接上图，这些表达式您能区分多少，请在评论区回答。文末高锋老师会给出答案。

庞杂的公式

我们的记忆树如下：两句话记忆对称性周期性：

记忆树

一函数型对称性，证明的方法就是记忆方法。解析过程如下：( )内相加为定值指的是(x+a)+(b-x)等于定值a+b，只要判断出这一点，我们就得到这个表达式表示的是对称性。由第一个表达式算出中点坐标，发现中点恒为定值。当x跑完定义域内的所有值，得到f(x)的图像，继而得到图像也关于改点对称。同样第二个表达式一样分析。

一函数型对称性

双函数型对称性，证明过程既是记忆方法。解析过程如下：这个地方为什么不能像一函数中那样加减呢。是因为一函数型中的x是同一个x，双函数中x不一定是同一个x。所以要找出x1+a和b-x2的对应点x0,再带入中点坐标公式。

双函数型对称性

双函数型对称性的第二类：

双函数型对称性

下面我们来记一下周期性：

巧妙地利用笔画记忆，这方法真绝了！

很巧妙地类比等差数列与等比数列，简单

更巧妙地把1+变成4,1-变成2，轻松记住周期，厉害！

记忆方法同上。

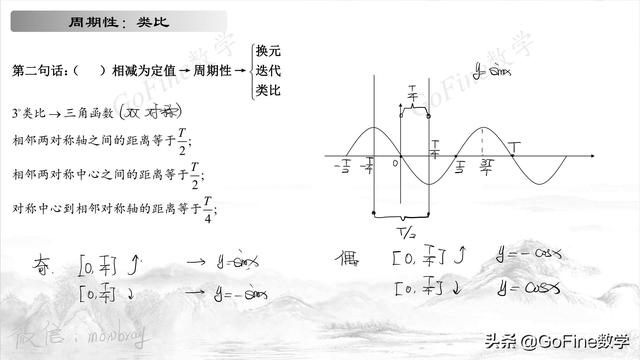
双对称函数的周期问题

再往下我们给出文首的答案，相信您现在

最后我们做一个知识汇总，相信您现在也能够轻松得到：

原创不易，如需转发，请注明GoFine数学。

各位同学，如果您喜欢老师的文章，请用您的行动“点赞”“转发”“关注”支持老师，非常感谢！