本文介绍了线性调频信号（chirp）的特性，指出其非平稳性质使得传统谱分析方法不适用。通过HHT（Hilbert-Huang变换）方法对两个部分重叠频带的chirp信号进行分析，成功分解出真实信号并展示Hilbert谱的高时间-频率分辨率。同时，与STFT、Wigner-Ville分布和小波变换进行对比，揭示了它们在时频分析中的优缺点。
3.1线性调频信号分析
线性调频信号(chirp)信号是一频率随时间呈线性关系连续变化的信号，其在时频谱图上应该为一正比例函数，由于其在各个局部时刻的频率都在变化，且每一时刻都对应着唯一的频率成分，它本身是一个典型的单分量信号也即固有模态函数，是一个非平稳信号，因此傅立叶变换等传统谱分析方法对其无能为力。
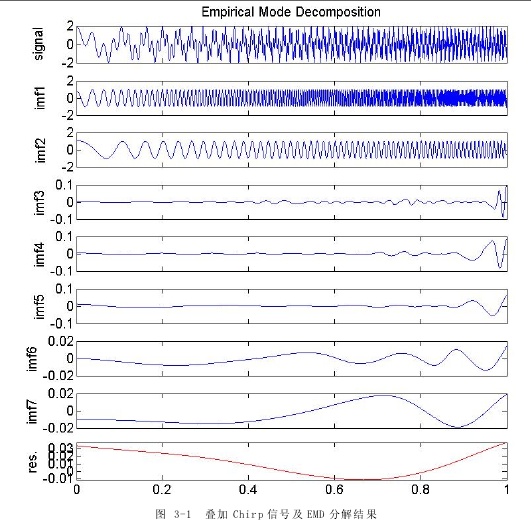
我们用HHT分析方法对两个叠加的 chirp 信号进行仿真，第一个chirp信号的起始频率为20Hz，截止频率为370Hz。第二个chirp信号的起始频率为3Hz，截止频率为120Hz。模拟信号的采样频率为2000Hz，可以注意到，这两个chirp信号的频带是部分重叠的，图 3-1 是chirp信号波形及其EMD分解结果。
从分解结果可以看出，一共得到七个 imf 分量，EMD 成功的分解出了两个频带部分重叠的chirp信号，imf1对应着第一个高频的chirp信号，imf2对应着第二个chirp信号。imf3到imf7幅值和频率都非常小，是分解过程中筛选出的虚假分量，并不包含原始信号的频率信息。
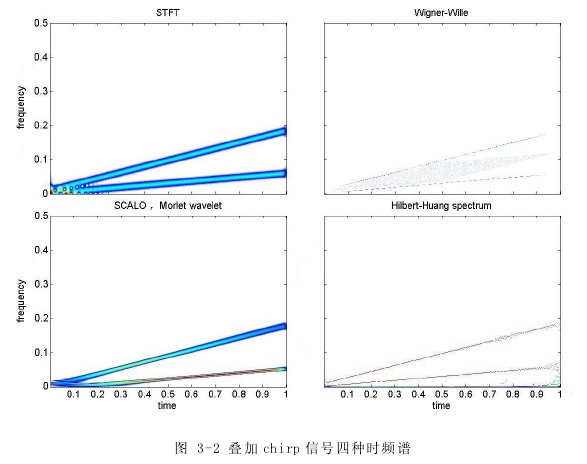
对各imf分量求解瞬时频率可以得到信号的时频谱，即Hilbert谱。图 3-2 示出Hilbert谱分析结果，两条斜率不同的直线反映出两个 chirp 信号各自的频率随时间连续变化情况。不仅反映出了信号中的频率范围，还提供信号中具体的局部频率信息，Hilbert谱具有很高的时间与频率分辨率。同时，在低频段出现了无关的频率成分，还有在时频线右端点出现了能量发散的情况，理想中应该是一条直线。前者是由虚假分量造成的，后者是由HHT的端点问题造成的，后面章节我们将针对这两个问题进行讨论，采取适当的方法处理。
为了与其它时频分析方法进行比较，图 3-2 中也同时给出了STFT变换、Wigner-Ville 分布和小波变换常规方法的时频分析结果。从时频谱来看，这三种方法都能够分析得到组成叠加信号的两个 chirp 分量，STFT变换和小波变换都存在时频分辨率的问题，且在低频段，由于频率比较接近，谱线发生重叠变形的情况，使得分析效果变差；而Wigner-Ville分布虽然两条 chirp 信号的谱线比较清晰，时频分辨率也足够好，但其交叉项的干扰也是比较严重的。
《来源科技文献，经本人分析整理，以技术会友，广交天下朋友》
扫一扫
7721
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
