有时候,我们会求一个数的算术平方根,而我们基本可以确定这个数就是一个完全平方数,而手头又没有计算器,怎么办?
办法有很多,最简单粗暴的办法就是:试!
100以内的完全平方数,我们在小学学乘法口诀的时候就很熟悉了,而我们通常接触的完全平方数一般也不会超过10000。因此,我们这里考虑的就是100到10000之间的完全平方数。怎样快速定位这个算术平方根呢?
我们很容易就能想到,它的算术平方根是两位数,因此,我们就分别考虑算术平方根的十位和个位。下面我们以完全平方数5329为例说明这个过程。
(1)首先,我们考虑算术平方根的十位。
我们知道,10的平方是100,20的平方是400,……70的平方是4900,80的平方是6400,90的平方是8100,而5329在4900和6400之间,因此它的算术平方根的十位是7。
(2)其次,我们考虑算术平方根的个位。
我们知道,一个数的个位决定了它的平方的个位。我们不妨列出表格:
数的个位 平方的个位
1,9 1
2,8 4
3,7 9
4,6 6
5 5
对照这个表格,我们可以发现,同一个平方数的个位,它的算术平方根的个位可能是两个,而这两个数的和是10。
5329的个位是9,因此它的算术平方根的个位可能是3,也可能是7。也就是说5329的算术平方根可能是73,也可能是77。
那到底是73,还是77呢?验算一下就是了:73的平方是5329,77的平方是5929。也就是说,5329的算术平方根是73。
好了,方法就这样,简单粗暴

 。
。
【补充】
我们知道,一个两位数个位如果是5的话,计算平方的时候只需要把十位数跟比它大1的数字相乘,然后在后面写上25,即:
15²=1×2×100+25,25²=2×3×100+25……
这样,我们只要把一个数跟个位是5的数的完全平方比较,就可以知道它的算术平方根的个位比5大还是比5小了。
还以上面的5329为例,我们很容易得到75²=7×8×100+25=5625,5329<5625,因此5329的算术平方根可能是73而不可能是77。
往期文章:
【初二】完全平方数有什么特点
【彩蛋】笔算开平方
笔算开平方跟竖式除法很像,这里只强调开平方跟竖式除法的不同,不太清楚的地方比照竖式除法和下面的示例。
(1)像竖式除法那样写出被开方数和根号。
(2)开方和除法的一个不同是除法每次往后写一位,开方是每次往后写两位,因此,首先从小数点向左向右给被开方数(习惯上用撇号)分节,每两位数一节(小数后如果位数不够要补0),开方结果的小数点跟被开方数的小数点对齐。
(3)找出不大于最左边那节数字的最大完全平方数,把它的算术平方根写到商的位置,把它写到被开方数的最左边那节数字的下边,像除法一样做差。
(4)跟除法不同的是开方时除数不固定,每次都需要计算除数。计算办法是用已经得出的开方结果(忽略小数点)乘以20再加上商。因为这时商还不知道,所以可以像除法那样试商,直到找到合适的商。习惯上把这个除数写在对应的被除数的左边,用竖线分隔;把商写到被开方数对应分节的上方。
(5)如果被开方数不是完全平方数,可以像除法那样补0一直除下去,不过开方每次是补两个0。
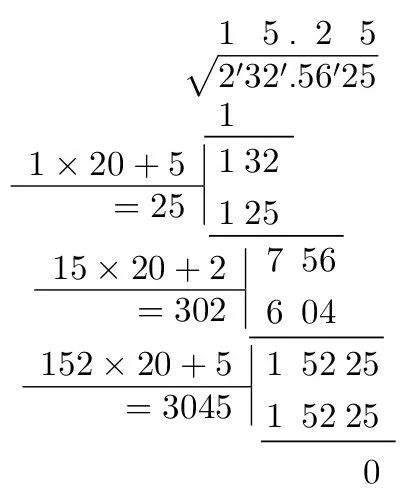























 286
286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








