smoothstep函数_OpenGL-Built–In Math Functions(内置数学函数)

周一到周五，每天一篇，北京时间早上7点准时更新~

跟着我们一起一天天进步，一步一步变成业界大佬。当别人在炫技术的时候，我们来手把手教你那些技术怎么实现。

GLSL supports many built-in functions to perform mathematical operations and to manipulate data in variables. The common math functions include abs(), sign(), ceil(), floor(), trunc(), round(), roundEven(), fract(), mod(), modf(), min(), and max(). For the most part, these functions operate on vectors as well as scalars, but otherwise behave like their counter parts in the C standard libraries. The roundEven() function doesn’t have a direct equivalent in C—this function rounds its argument to the nearest integer, but breaks ties when there is a fractional part of 0.5 by rounding to the nearest even number. That is, 7.5 and 8.5 will both round to 8, 42.5 will round to 42 and 43.5 will round to 44.

GLSL支持很多内置的执行数学操作的函数。这些就包括常用的abs(), sign(),ceil(), floor(), trunc(), round(), roundEven(), fract(), mod(),modf(), min(), 以及 max()。大部分时候，这些函数都可以用来操作 向量以及标量，但是他们计算的时候会表现得跟C语言的库很相似。

Two implicit declarations of the clamp() function are

两个隐式申明的clamp函数如下所示：

vec4 clamp(vec4 x, float minVal, float maxVal);
vec4 clamp(vec4 x, vec4 minVal, vec4 maxVal);

This function clamps the incoming vector x to the range specified by minVal and maxVal (which may be scalars or vectors). For example, specifying minVal to be 0.0 and maxVal to be 1.0 constrains x to be in the range 0.0 to 1.0. This is such a common range to which to clamp numbers that graphics hardware often has a special case for this range, and some shading languages even include a built-in function specifically to clamp inputs to this range.

这个函数会把输入的x参数截断到minVal到maxVal的范围内。比如minVal是0.0，maxVal是1.0，则x会被约束在0.0到1.0之间。通常情况下，图形硬件经常需要在一些场景下把数值约束在这个范围内，在一些着色器语言中甚至 包含了内置的函数去把输入约束在这个范围内。

A few more special functions are mix(), step(), and smoothstep(). mix() performs a linear interpolation between two of its inputs using the third as a weighting factor. It can effectively be implemented as

还有一些函数，比如mix(), step(), 和 smoothstep()。mix函数执行的线性插值，输入的前俩参数是插值的起点和终点，第三个参数是权重。它的算法如下：

vec4 mix(vec4 x, vec4 y, float a){
	return x + a * (y - x);
}

Again, this is such a common operation in graphics that it is a built-in function in the shading language and graphics hardware may have special functionality to implement this directly.

这些常用的内置在着色器语言里的操作可能会直接被图形硬件所支持。

The step() function generates a step function (a function that has a value of either 0.0 or 1.0) based on its two inputs. It is defined as

step函数会基于输入的两个参数产生一个返回值，这个返回值要么是0.0要么是1.0

vec4 step(vec4 edge, vec4 x);

It returns 0.0 if x < edge and 1.0 if x >= edge.

如果x≤edge,则返回0.0，否则返回1.0。

The smoothstep() function is not as aggressive and produces a smooth fade between two of its inputs based on where the value of its third lies between the first two. It is defined as

smoothstep函数执行的则是一个平滑的过渡操作，输入的参数前两个是起始点和终点，最后一个参数是一个影响因素，会根据这个东西插值出一个值，它的函数申明是：

vec4 smoothstep(vec4 edge0, vec4 edge1, vec4 x);

smoothstep() can effectively be implemented as

smoothstep的算法如下：

vec4 smoothstep(vec4 edge0, vec4 edge1, vec4 x){
	vec4 t = clamp((x - edge0) / (edge1 - edge0), 0.0, 1.0);
	return t * t * (vec4(3.0) - 2.0 * t);
}

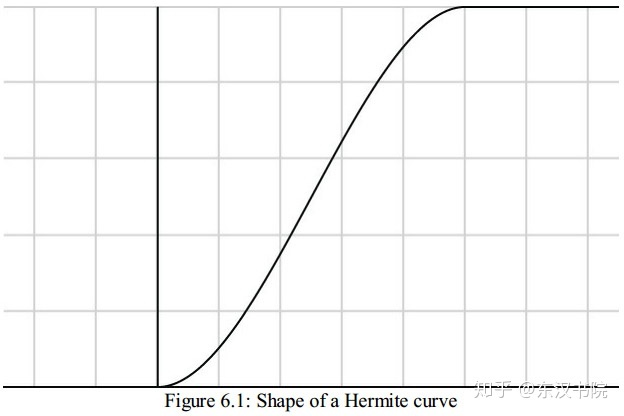
The shape produced by smoothstep() is known as a Hermite curve and the operation it performs is Hermite interpolation. The general shape of the curve is shown in Figure 6.1.

smoothstep产生的图像被叫做哈米特曲线，它的操作叫做哈米特插值。通常情况下这个曲线长相如图6.1所示：

The fma() function performs a fused multiply–add operation. That is, it multiplies the first two of its parameters together and then adds the third. The intermediate result of the operation is generally kept at a higher precision than the source operands, producing a more accurate result than if you were to write those two operations directly in your code. In some graphics processors, the fused multiply–add function may be more efficient than a sequence of a multiplication followed by a separate addition operation.

fma函数执行的是乘完后相加的操作。也就是说，它把前两个参数相乘后再加上第三个参数。这个函数与你直接在代码里面写这个算法的区别就在于，它的中间结果会比你在普通代码中执行乘法时的精度更高，这样一来最终结果 的精确度就相对更高了。在一些图形处理器里，fma函数比你直接在普通代码里实现这个算法更加的高效。

Most of the math functions in GLSL presume that you are using floating-point numbers in the majority of your shader code. However, there are a few cases where you might be using integers, and GLSL includes a handful of functions that are designed to help you perform arithmetic on very large integer (or fixed-point) numbers. In particular, uaddCarry() and usubBorrow() allow you to perform add with carry and subtract with borrow operations, and imulExtended() and umulExtended() allow you to multiply a pair of 32-bit signed- or unsigned-integer values together, respectively, producing a 64-bit result as a further pair of 32-bit values.

很多GLSL种的数学函数嘉定你使用的是浮点数。然而，在一些情况下，你可能想使用整数，GLSL其实也有很多来帮助你实现整形运算的函数。特别是uaddCarry()和usubBorrow()函数可以让你在执行add的时候执行进位以及在 执行减法的时候执行借位操作，imulExtended() 和 umulExtended()函数可以让你执行32位有符号或者无符号整型相乘的时候产生一个64位的返回值。

In addition to all this low-level arithmetic functionality, GLSL includes support for all of the expected trigonometry functions, such as sin(), cos(), and tan(); their inverses, asin(), acos(), and atan(); and the hyperbolic forms of those functions, sinh(), cosh(), tanh(), asinh(), acosh(), and atanh(). Exponentional functions are also included: pow(), exp(), log(), exp2(), log2(), sqrt(), and inversesqrt(). Because most of the GLSL functions dealing with angles work in radians, even though sometimes it might be convenient towork in degrees, GLSL also includes the radians() function (which takes an angle in degrees and converts it to radians) and the degrees() function (which takes an angle in radians and converts it into degrees).

额外的，GLSL还支持所有的取反操作，比如：sin(), cos(), and tan()的取反操作asin(), acos(), 和 atan()。以及它们对应的双曲线形式：sinh(), cosh(), tanh(), asinh(), acosh(), 和 atanh()。 幂指函数也同样是被GLSL直接支持的：pow(), exp(), log(), exp2(),log2(), sqrt(), 和 inversesqrt()。由于大部分GLSL函数需要输入的是弧度而不是角度，即便有时候角度使用起来更舒服，所以GLSL也包含 radians函数以及degrees函数。

本日的翻译就到这里，明天见，拜拜~~

第一时间获取最新桥段，请关注东汉书院以及图形之心公众号

东汉书院，等你来玩哦