c++矩阵连乘的动态规划算法并输出_【CUCS算法连载】图论 动态规划与记忆化搜索（三）...

Author: Lemmore

Introduction

前两章介绍了动态规划问题的主要解题思路，包括构建子问题和推导状态转移公式。大家可以利用这种思路解决绝大部分动态规划问题，也可以把这种思路当做参考想出适合自己的解题方式。值得注意的是一些较为复杂的问题的解法往往需要把动态规划和其它算法结合起来，这一章就来讲解几个这样的例子。对于每个例子推荐大家先思考一下，需要线索的话可以参考一下提示，最后再看解法。

★

Leetcode 401. Split Array Largest Sum

题目链接: 

https://leetcode.com/problems/split-array-largest-sum/

问题描述:

给定一个一维数组和一个值k，数组中每个数字均为非负整数。要求把数组分成k份(即每份都连续)非空数组，使得每份的数字和最大值最小，并输出该最小值。

样例输入: [1, 9, 5, 8, 0, 8, 2, 9], k = 3

样例输出: 11

解释: 将原数组分为[1, 9, 5], [8, 0, 8], [2, 9]，每份数字和分别为15，16，11，这些数字和中最大值为16，在所有可能的分组中最小。

提示:

动态规划 + 前缀和 + 二分搜索

解法:

我们可以把这道题看做在n个数之间放k - 1个挡板。假设这些挡板按从左到右的顺序摆放，如果左侧有j个挡板已经放好(0 ≤ j < k - 1)，那么找出第j + 1个挡板的最佳位置就是一个在第j个挡板右侧第一个数字到第n个数之间线性搜索的过程。

在动态规划系列第一章我们提到了先想递归再想去重的思路，从上述内容不难发现我们找到了一个时间复杂度为O(k^n) * O(n)的递归思路，现在问题在于如何去重。通过仔细的观察我们发现，在上面提到的线性搜索过程中有两个可以优化的地方：

(1) 由于前j个挡板已经放好(即前j组已固定)，前j组的数字和中的最大值不会变动，存下来可以避免重复计算，即动态规划，可以把时间复杂度从O(k^n)降为O(kn)；

(2) 计算第j + 1组的数字和不需要遍历累加第j个挡板和第j + 1个挡板之间的数字，用前缀和(详细介绍见文末链接)替代可以把时间复杂度从O(n)降为O(1)。

综上所述，我们将用二维矩阵dp[i][j]记录将前i个数字分为j组的最优解，并利用前缀和优化每次数字和的计算成本。类似动态规划系列第二章的Frog Jump问题，本题状态转移公式同样可以从一对多和多对一两个角度考虑，要么用dp[i][j]的值去更新所有dp[x][j+1]的值(i+1 ≤ x ≤ n)，要么用所有dp[x][j-1]的值(1 ≤ x ≤ i-1)去更新dp[i][j]的值。一般两种方法复杂度没啥区别，这里我们选择后者，因为后者进一步优化更方便。令sum(x+1, i)为原数组第x+1个数到第i个数的数字和，后者状态转移公式为dp[i][j] = min(max(dp[x][j-1], sum(x+1, i)))，此时时间复杂度为O(kn)。

还能优化吗？还能优化。通过更仔细的观察我们发现，上述状态转移公式中随着x的增加，dp[x][j-1]单调递增，sum(x+1, i)单调递减。这意味着我们可以使用二分搜索快速确定第j个挡板的位置，当dp[x][j-1] < sum(x+1, i)时向右侧搜索，当dp[x][j-1] > sum(x+1, i)时向左侧搜索。这样一来时间复杂度即可降为O(k lgn)。

相关问题

登山

http://noi.openjudge.cn/ch0206/1996/

ZOJ 1074. To the Max

题目链接:

https://vjudge.net/problem/ZOJ-1074

问题描述:

给定一个二维数组，数组中每个数字均为整数。要求在该数组中找出一个非空子矩阵，使得该子矩阵中所有元素之和在所有非空子矩阵中最大，输出该子矩阵的所有元素之和。

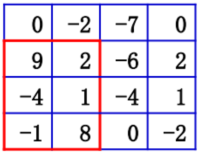
样例输入: 下图中4x4矩阵

样例输出: 下图红框中3x2矩阵

解释: 红框所示子矩阵所有元素之和为15，为所有非空子矩阵中最大元素和

(from CSDN)

提示:

动态规划 + 前缀和 + 最大子序列和

解法:

如何定义一个子矩阵呢？我们可以通过给定行数区间和列数区间来确定一个子矩阵，即这个子矩阵从第i行到第j行，从第x列到第y列，共四个变量。如何计算nxn矩阵和呢？遍历所有元素求和需要O(n^2)的时间复杂度。这样一来我们就得到了一个时间复杂度为O(n^6)的解法，解完了。

好吧并没有，把这个解法说给面试官可能会被鲨，那我们还是想想怎么优化吧。关于求和的优化基本都用到类似前缀和的思想，在多维求和问题中，前缀和化O(n)为O(1)的性质还起到矩阵降维的作用。我们首先对原矩阵的每一列都进行前缀和计算的预处理，时间复杂度为O(n^2)；接着以O(n^2)的时间复杂度遍历原矩阵的行数区间(即原矩阵第i行到第j行)，在每个区间内利用前缀和以O(n)的时间复杂度算出每列的元素和。这样一来，固定行数区间下计算不同列数区间的子矩阵最大元素和就转化为：在一维数组中找出最大子序列和。

最大子序列和的解法很简单，利用了一点动态规划的思想，即从左到右遍历数组，不断累加并不断更新最大累加和，中途一旦累加和为负数，则累加和归零继续遍历。因此最大子序列和时间复杂度为O(n)，结合上述时间复杂度，原题解法总时间复杂度为O(n^2) + O(n^2) * (O(n) + O(n)) = O(n^3)。

相关问题:

最大矩形

https://leetcode.com/problems/maximal-rectangle/

NOIP 2017. 逛公园

题目链接:

https://www.luogu.com.cn/problem/P3953

问题描述:

给定一个值k和一张n个点m条边构成的有向图，其中第一个点为起点，最后一个点为终点。该有向图每条边有一个非负权重，且没有自环和重边(既存在从顶点A到顶点B的边又存在从B到A的边)。要求找出所有从起点到终点的不重复路径(最短路长度记为d)，使得该路径所有权重之和不超过d + k。

输入格式: 第一行包含三个整数 n, m, k。接下来m行，每行三个整数 ai, bi, ci，代表编号为ai, bi的点之间有一条权值为ci的有向边。

输出格式: 输出不重复路径的总数。如果有无数条路则输出-1。

提示:

动态规划+ 最短路 + 深度优先搜索

解法:

不难看出这题肯定要用到最短路算法。此外，计算从起点到终点的不重复路径似乎有些熟悉，让人联想到“在mxn网格中，每次只允许向右或向上走一格，问从左下角到右上角一共有多少种走法”的问题(这似乎是作者最早接触过的动态规划问题，不知道大家小学学数学有没有做过这个题hhh)。要解决这个问题，我们可以给每个格子标出到该格子有几种走法，由该格子左边和下边的相邻格子的走法数相加而得。把这个问题中的“只允许向右或向上走一格”替换为“只允许向以该顶点为起点的有向边的终点移动”，本题的动态规划思路就呼之欲出了。

对于每个顶点我们可以记录到该顶点有多少种不重复路径，但仅仅如此却无法对“路径所有权重之和不超过d + k”的这一要求作出筛选。要满足这个条件，最直接的方法就是在动态规划中用额外的维度来记录这一变量：令二维矩阵dp[i][j]记录从起点到顶点i时路径权重和(以下记为路径长度)为j的不重复路径数量。为了节约空间，j的含义可以改为“路径长度为d+j”，其中d为起点到顶点i的最短路的长度。

那么状态转移公式如何设计呢？通过观察我们发现，在所有符合题目条件的路径中，排除最短路和带零环的最短路(即所有边权重为零的环)，其它路径可以看做在一些边上分配了额外长度，这些额外长度之和不超过k。令d(a)为起点到顶点a的最短路，w(a, b)为顶点a到顶点b的边权重。对于一条从顶点x到顶点i的边，w(x, i) - (d(i) - d(x))为该边的额外长度(为了增加可读性用e表示)，由此推出状态转移公式为dp[i][j] = dp[x][j-e]。

整理一下思路，我们首先需要算出从起点出发到所有边的最短路，这一步可以采用Dijkstra算法；其次我们列出二维矩阵dp[i][j]记录从起点到顶点i时路径长度为d+j的不重复路径数量；最后我们通过dp[i][j] = dp[x][j-w(x, i)+d(i)-d(x)]自起点向终点枚举路径长度更新dp，并输出抵达终点n时所有额外路径长度不超过k的不重复路径数，即sum(dp[n][j]), 0 ≤ j ≤ k。算法总时间复杂度为O(kn^2)。

但如果有很多顶点到不了终点或者即使到了终点总长度也超标，之前不就白算了？还有如果出现了有效零环(即有无数个解)那整个算法不就无限循环了？而且总觉得这个枚举法蠢蠢的。考虑到这些问题，我们可以分别通过

(1) 把所有边反过来(即交换起终点)形成反图并计算终点到各个点的最短路来排除一些顶点；

(2) 通过建立和dp大小相同的二维矩阵visit[i][j]来记录访问状态排查有效零环(如果零环所在的路径本身就超过限定长度则无效，可用正反图最短路判断)；

(3) 把枚举法改为从终点开始沿反图进行深度优先搜索来更新二维矩阵dp(这样一来只需要访问dp中的部分元素)

来解决零环问题并优化。优化后算法的时间复杂度计算就当做练习吧！

相关问题:

骑士游戏

https://www.luogu.com.cn/problem/P4042

IOI 2005. 河流

题目链接:

https://www.luogu.com.cn/problem/P3354

问题描述:

在Byteland国，有N个伐木的村庄，这些村庄都座落在河边。目前在Bytetown，有一个巨大的伐木场，它处理着全国砍下的所有木料。木料被砍下后，顺着河流而被运到Bytetown的伐木场。Byteland 的国王决定，为了减少运输木料的费用，再额外建造K个伐木场。这K个伐木场将被建在其他村庄里。这些伐木场建造后，木料就不用都被送到Bytetown了，它们可以被运输到第一个碰到的新伐木场处理。显然，伐木场座落的村子就不用再付运送本村木料的费用了，这些木料可以直接被本村的伐木场处理。国王的大臣计算出了每个村庄每年要产多少木料，你的任务是决定在哪些村庄建设伐木场能获得最小的运费。其中运费的计算方法为：每一吨木料每千米1分钱。

输入格式：第一行包括两个正整数N和K，N为村庄数，K为要建的伐木场的数目，其中K ≤ N。除了Bytetown外，每个村依次被命名为 1, 2, 3, …, n，Bytetown被命名为0。

接下来N行，每行3个数：非负整数wi为每年i村产的木料的块数；非负整数vi为离 i 村下游最近的村子(即i村的父结点)；正整数di为vi到i的距离(千米)。

输出格式：输出最小花费，精确到分。

提示:

动态规划 + 多叉树转二叉树 + 深度优先搜索

解法:

显然，把村庄看做节点，把河流看做边，把Bytetown看做根节点，这是一个树形DP问题。乍一看的确很难，那就从简单的例子入手。如果我们在i节点(非根节点)建造伐木场，对总花费的影响为：以i节点为根节点的子树上所有木料不再需要运送从节点i到Bytetown的距离。同时我们观察到，如果已知以i节点为根节点的子树上所有伐木场的分布，那么不难算出i节点建造伐木场和不建造伐木场两种情况下的最小花费。据此可以想到

(1) 列出二维矩阵dp[i][j]来记录以i节点为根节点的子树上分配j个伐木场的最小花费；

(2) 计算出每个节点到根节点的距离以及每个节点为根节点的子树上的木料总量作为优化(避免重复计算)。

但这样一来会有一个问题：我们无法确定i节点到Bytetown这条路径上的伐木场分布，而这条路径上离i节点最近的伐木场位置将影响到以i节点为根节点的子树上的全局最优伐木场分布。举个例子：假设以i节点为根节点的子树上的局部最优伐木场分布中所有伐木场都离i节点隔着很多生产大量木料的村子，但因为这些村子离i的距离几乎为零所以影响不大。此时如果i节点没有伐木场，而Bytetown是i节点上游唯一的伐木场且离i节点非常远，那么运输这些村子生产的大量木料就会非常昂贵。

和上题类似，最直接的解决方法就是在动态规划中用额外的维度来记录每个节点上游最近的伐木场位置。上述二维矩阵dp[i][j]现在更新为三维矩阵dp[i][j][k]，其中i表示当前节点，j表示离i最近的上游伐木场位置，k表示以i节点为根节点的子树上分配有k个伐木场。

按照惯例，构建子问题的下一步是推出状态转移公式。但推导公式之前，在这种既要考虑下游又要考虑上游的情况下，该以什么顺序更新dp呢？首先我们观察到计算上游伐木场的花费需要知道下游伐木场的分布，因此节点的遍历顺序是从下游到上游。对于每个节点的花费计算，我们需要知道该节点所有子节点的花费。我们都知道有两种普遍的遍历方法：深度优先搜索和广度优先搜索(详细分析见“图论 - 基础搜索算法”)。如果采用深度优先搜索，则每个节点无法直接和自己的兄弟节点联系(需要记录额外信息)，共同向父节点传递信息；如果采用广度优先搜索，则需要存储全图所有节点信息才能抵达最下游。所以这里涉及到一个有趣的方法：多叉树转二叉树(方法如下图，详细步骤见

https://blog.csdn.net/C20180602_csq/article/details/70738280)。

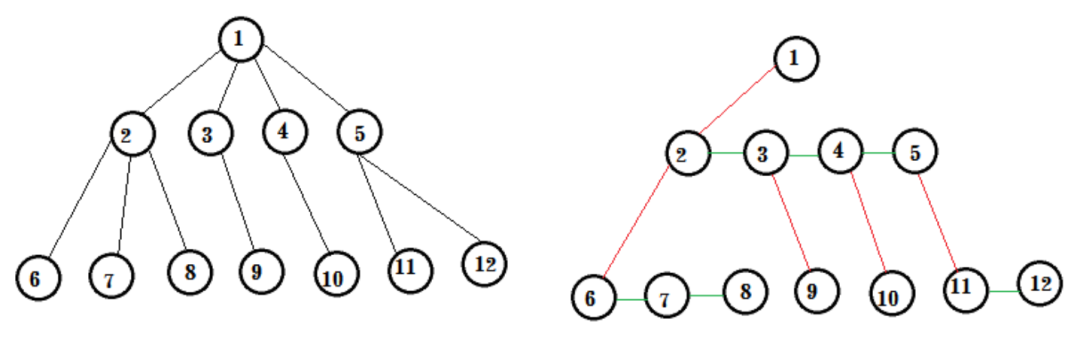
(from 博客园)

将题目中的多叉树转为二叉树后我们发现每个节点可以直接获取所有兄弟节点的信息，且在二叉树中可以采取深度优先搜索遍历来节约空间成本。对于多叉树的每个节点，我们需要枚举k个伐木场在所有子节点中的分配；但对于转换后二叉树的每个节点，我们只需要枚举k个伐木场在左子节点(多叉树中的儿子节点)和右子节点(多叉树中的兄弟节点)之间的分配。令l为分配给左子节点的伐木场数量：

(1) 若i节点处不建伐木场，k - l为分配给右子节点的伐木场数量；

(2) 若i节点处建伐木场，k - l - 1为分配给右子节点的伐木场数量。

确定了i(当前节点)，k(伐木场数量)，l(枚举分配给左子节点的伐木场数量)三个维度的遍历方法后，只要在i和k两层循环之间加上j(离i最近的上游伐木场节点)的遍历即可，也就是假设每个上游节点j为离i最近的上游伐木场的情况。

所有维度的遍历顺序确定后就可以推导状态转移公式了。令left, right分别为转换后二叉树上节点p的左子节点和右子节点，则有

(1) 在p节点建造伐木场：dp[p][j][k] = min(dp[p][j][k], dp[left][p][l] + dp[right][j][k-l-1])

(2) 不在p节点建造伐木场：dp[p][j][k] = min(dp[p][j][k], dp[left][j][l] + dp[right][j][k-l] + p节点产生的木料运到j节点的费用)

最终答案为Bytetown子树上的最小花费以及剩余木料运到Bytetown的花费之和，即dp[Left][0][K]，其中Left为Bytetown在转换后二叉树上的左子节点。总时间复杂度为O(KN^2)。

相关问题:

战略游戏

https://www.luogu.com.cn/problem/P2016

以上四个例子主要讲述的是动态规划在不同环境下的应用(数列、矩阵、图、树)以及与其它算法的结合(前缀和、二分搜索、最短路、深度优先搜索、多叉树转二叉树)，希望能帮助大家更深入地理解动态规划(如果是巨佬当我没说x)。

那么动态规划专题到这里就告一段落了。除了以上四道题所涵盖的类型，尼姆游戏也是一个很有趣的专题，和动态规划关系密切。要是有人对尼姆游戏感兴趣可以在评论区留言，作者看情况加更一章(手动狗头)。

相关材料：

前缀和详解

https://blog.csdn.net/myRealization/article/details/104470754

往期内容：

【CUCS算法连载】图论 - 动态规划与记忆化搜索(二)

【CUCS算法连载】图论 - 动态规划与记忆化搜索(一)

【CUCS算法连载】算法分析 - 算法分析简介

【CUCS算法连载】图论 - 拓扑简介(二)

【CUCS算法连载】图论 - 拓扑简介(一)

【CUCS算法连载】图论 - 基础搜索算法

结语

以上内容仅代表作者个人看法，如有错误欢迎指正。觉得有用或者有建议的话欢迎在评论区交流！对算法有兴趣的朋友可以联系我一起学习 :D

作者邮箱：

leuchteintraum@outlook.com