hive值乘以0.01保留一位小数_为什么最简分数的分母中除了2、5以外，不含其他质因数，这个分数就能化成有限小数？...-CSDN博客

本文链接：https://blog.csdn.net/weixin_39798626/article/details/112373048

DAO YU

导语

我们都知道判断一个最简分数能否化成有限小数，只要看其分母中是否含有2、5以外的质因数，如果不含就可以化成有限小数，反之则不行。但是在教学中如何让学生真正明白其中的道理呢？下面我想通过多版本教材比较，结合实践谈谈自己的看法。

JIE DA

解答

在学习《分数和小数的互化》时，各版本教材在方法上，主要引导学生运用分数与除法的关系，即用分子除以分母求商的方法，将分数化成小数。通过这种方法，学生发现分数转化成小数会出现两种情况：一是能除得尽，化成有限小数；二是除不尽，在结果的小数位数处理上，一般保留两位或三位小数。

|| 人教版

|| 北师大版

|| 苏教版

人教版教材在该内容练习后面以“你知道吗”介绍怎样的最简分数能化成有限小数的判断方法，即只要最简分数的分母只含有质因数2和5，就可以化成有限小数，如果分母含有2和5以外的质因数，这个分数就不能化成有限小数。

-01-

思考一：为什么要有最简分数这个判别前提呢？

我们知道，任何分数都可以根据分数的基本性质，通过将分数的分子和分母同时乘以同一个数(0除外)，使分母和分子含有某个因数。

以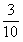为例，我们将分子与分母同乘3得到。的分母中含有2、5以外的质因数3，那么它就无法化成有限小数了吗？显然不是。因为分子中也有质因数3，我们可以通过约分，把质因数3化简掉，变成最简分数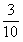，也就是0.3。

所以，离开最简分数这个前提，单纯地看分母中是否含有某个质因数是没有意义的。因此，要判断一个分数是否能化成有限小数，必须基于最简分数这个判别前提。

明师之道

教师说理专栏

-02-

思考二：可以怎样理解最简分数能化成有限小数的判断方法呢？

我们可以基于数学本质的视角，从分数与小数之间的关系来探讨其中的奥秘。

学生在四年级时就已经学过小数的意义，即“一位小数、两位小数、三位小数……分别表示十分之几、百分之几、千分之几……”。

根据这一意义，分母是 10、100、1000……的分数就可以直接改写成小数。同样的道理，能化成有限小数的最简分数，也可以运用分数的基本性质，将其还原为十进分数，进而改写成小数。

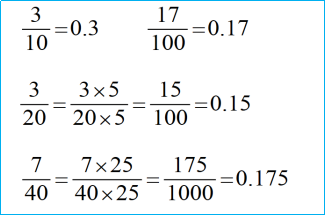
我们可以用分解成质因数相乘的形式来进一步具体分析。

1个2乘1个5得10,10乘10得100。当分母是20时，已经有2个2和1个5，那么只要将分子分母同乘一个5，就可以将20凑成整百转化为分母是100的分数，从而直接改写成两位小数。用同样的方法，也可以将转化为分母是1000的分数，进而改写成三位小数。

如果分母中含有除2和5以外的质因数，会出现什么样的情况？以为例，我们在尝试将它转为化十进分数时，会发现：，2乘5得10，可是没有一个整数和3相乘得10，这样就无法把这个分数转化为分母是10、100、1000……的分数，也就无法改写成有限小数。

因此，当最简分数的分母中只含有质因数2与5时，分母就是10、100、1000……这些数的因数，那么我们就能利用分数的基本性质，将它转化为十进分数，进而改写成小数。

其实，无论是将分数转化为十进分数，还是把分子除以分母，两种算法从本质上来说，算理是相通的，都可以看作利用分数的基本性质将分数转化成分母是1、10、100、1000……的分数，再改写成小数。

明师之道

教师说理专栏

综上所述

分数化成小数主要有两种方法：一是通过分子、分母同乘以相同的数，转化成十进分数；二是用分子除以分母求商的方法。但是教材主要呈现第二种方法，这是因为第一种方法虽是巧算，但因其特殊也具有局限性，只适合判别，而第二种方法具有普遍性，无论能不能化成有限小数，我们都可以算出其结果(或近似值)。因此在教学中，我们是否可以进一步思考：

1.相对于教材只呈现用分子除以分母的方法，我们是否可以有效地扩大学生课堂探究空间，让学生经历分数化小数两种方法的形成过程，将一般情况和特殊情况进行整合，引导学生深入认识分数与小数的密切联系，加深对分数化小数基本原理的理解。然后再通过设置矛盾冲突，引导学生质疑为什么必须基于最简分数这个判别前提，进一步激发探究欲望，利用已有的知识经验——分数的基本性质，发现这背后的原因。

2. 经历自主探究转化方法的学习过程后，我们是否将两种方法进行比较，进一步做好算理的本源性沟通。让学生经历分数化小数的方法由特殊到一般的归纳过程，体会用一般方法的普适价值，同时也感受到特殊方法的简便性，学会根据不同情况选择不同的方法。

3. 基于教材安排，研究完小数与分数互化的方法后，教师是否可以进一步做好互化的一致性表达。如下图所示，有限小数化成分数和分数化成有限小数的方法其实是一个相通互逆的过程，通过程序化表达，让学生直观的感悟它们之间转化道理是一致的，进而形成更加简约、牢固的结构化理解，更好地促进学生的数学学习。

明师之道

教师说理专栏