leetcode 系列之-动态规划题型总结

动态规划问题一般性总结

动态规划的思想：把小问题的最优解组合一起可以得到整个问题的最优解。
动态规划题目通常用于解决计数类问题。常见有线性DP，区间DP，背包问题等。解决背包问题通常要明白下面几点。

1. 属性：Max / Min /数量 动态规划问题最终通常让求解某一问题的最大值，最小值，数量。出现这几个字段，我们就要考虑是否应用动态规划能够解决该问题。 比如说： 最大连续子序列和，最长不下降子序列。
2. 状态表示： 解决动态规划问题的一个关键点就是 状态表示，状态表示根据问题而变化，能根据状态，最终能求出问题的最优解。状态表示的本质就是记录子问题的解，来避免下次遇到相同子问题重复计算。比如说 状态 f [ i , j ] 表示从（1,1）走到（i，j）的路线上某一数量的最大值。在最大连续子序列和问题（下文介绍了最大连续子序列和问题中，我们用 dp[i] 表示以数组A[i] 为结尾的连续序列的最大和。最后的结果就是dp[0],dp[1] …dp[n-1] 的最大值。
   确定状态需要两个意识 :
   1 最后一步
   2 子问题
3. 状态转移方程：解决动态规划问题的另一个关键点就是状态转移方程，我可以将其看成对根据状态表示对集合进行划分。划分的依据可以是按照最后一步进行一个反推。划分的原则是不重复，不漏。对于最大连续子序列和问题，dp[i]的计算，因为是连续子列，要保证连续就只有两种可能:一种是数组A[i]单独一个值就可以达成最大条件，第二种是dp[i-1]+A[i] 为最大。所以其状态转移方程为：dp[i]=max({A[i],dp[i-1]+A[i]})

1 坐标型动态规划 : 给定一个序列或网格。 需要找到序列/网格中某条路径。 特点dp[i] 表示以ai 结尾的满足条件的子序列的性质。 eg: 礼物的最大值。 dp[i][j] 表示以下标(i,j) 结尾的满足条件的路径性质。
还有 最大连续子序列和，最长上升子序列。

2 序列型动态规划: 前i 个… 最小/方式数/ 可行性。
特点: 动态规划方程 f[i] 中下标前i 个元素 a[0],…a[i-1] 的某种性质。 eg: 最长公共子序列, 最长回文子串， 打家劫舍，股票问题。

3 划分性动态规划:
给定长度为N 的序列或者字符串 。要求将一个序列或字符串划分成若干段满足要求的片段。
解决方法：最后一步->最后一段
枚举最后一段的起点

如果题目不指定段数，用d[i]表示前i个元素分段后的可行性，最值，方式数
如果题目指定段数，用d[i][j]表示前i个元素分成j段后的可行性，最值，方式数
eg: 把数字翻译成字符串。dp[i] 表示num[0,1,…i] 能够翻译成字符串的种类数。

爬楼梯

分析： 求数量，考虑用动态规划。dp[n] 表示第n 阶台阶的跳法有多少种。状态转移方程dp[n]=dp[n-1]+ dp[n-2]。

public int climbStairs(int n) {
        if(n==1){
            return 1;
        }
        if(n==2){
            return 2;
        }
        int []dp=new int[n+2];
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

执行结果：

零钱兑换

题目描述

假设amount 为27
最后一步思考

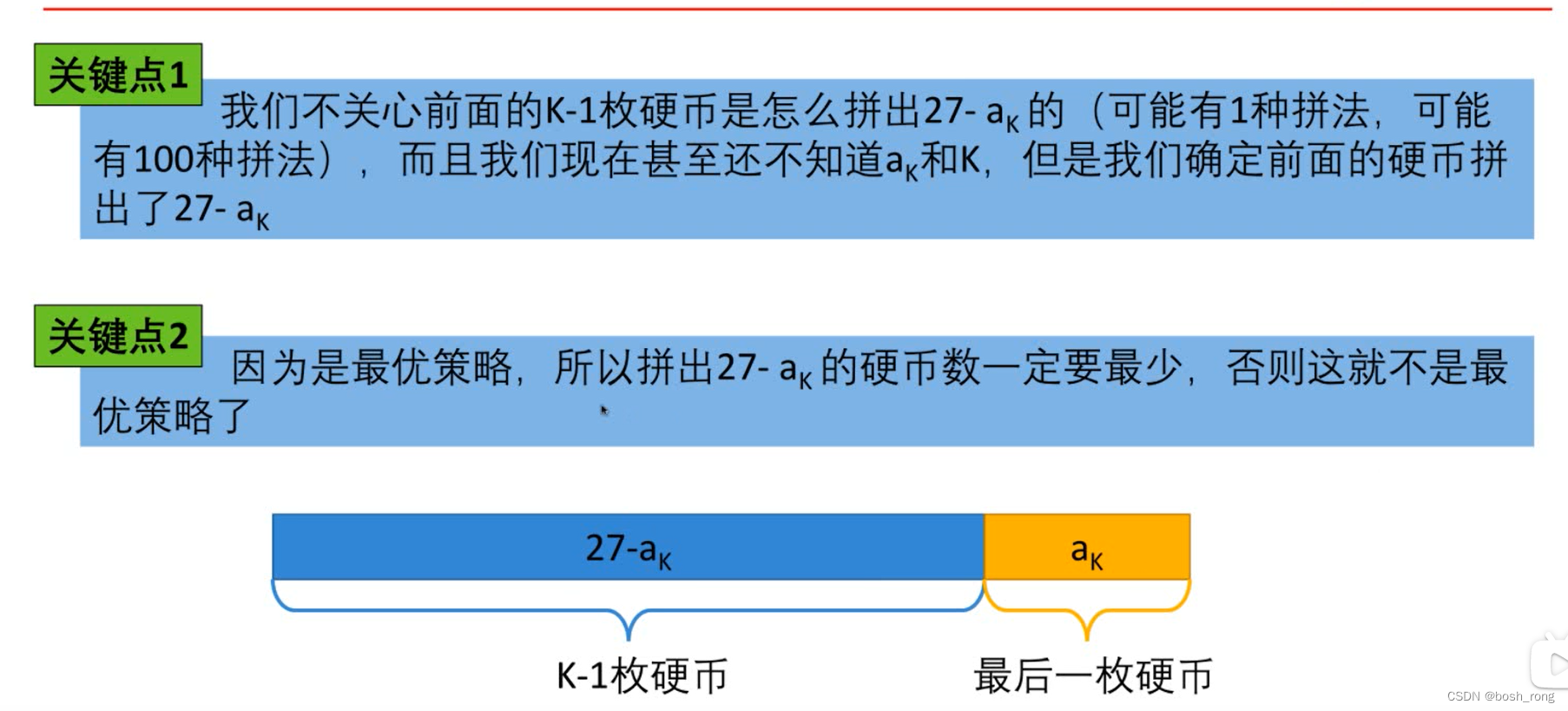
子问题


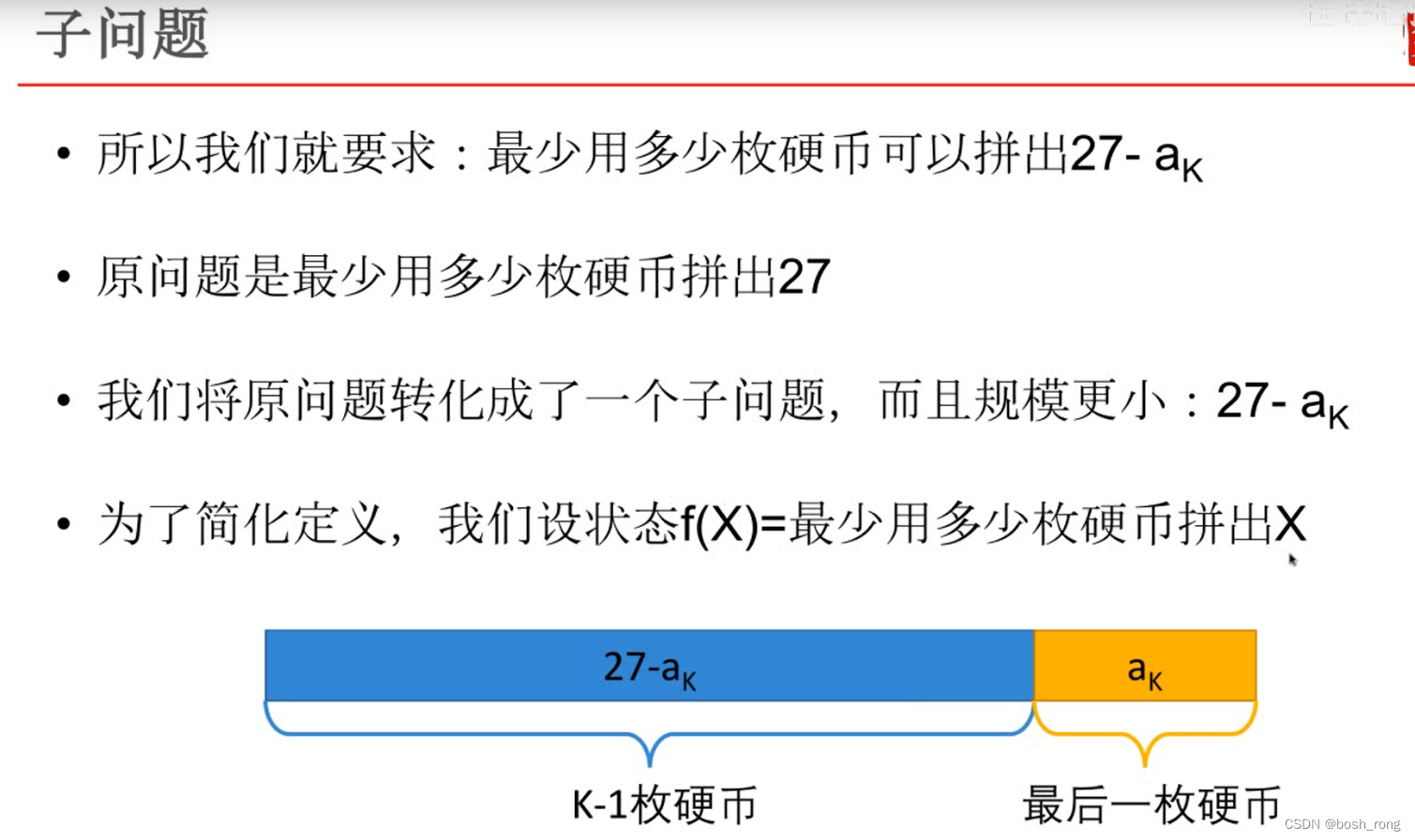
求问题 f(n)， 要知道子问题 f(n-i) 因此要先算 f(n-i)
状态表示 : dp[i] 剩余钱为i个的，能凑成的最少硬币个数。dp[i]=min(dp[i],dp[i-coins[k]]+1)， 一个是不选该硬币，一个是选该硬币。

public class 零钱兑换 {
    public int coinChange(int[] coins, int amount) {
        // 动态规划  完全背包
        // dp[i] 剩余钱为i个的，能凑成的最少硬币个数
        // dp[i]=min(dp[i],dp[i-coins[k]]+1)
        // 一个是不选该硬币，一个是选该硬币
        int [] dp=new int[amount+1];
        int lens=coins.length;
        dp[0]=0;
        for(int i=1;i<lens;i++){
            dp[i]=Integer.MAX_VALUE;
        }
        for(int i=1;i<=amount;i++){
            // 遍历所有硬币
            for(int k=lens-1;k>=0;k--){
                if(i>coins[k])
                  dp[i]=Math.min(dp[i],dp[i-coins[k]]+1);
            }
        }
        return dp[amount];
    }
}

最长不含重复字符的子字符串

题目描述：

解题思路：感觉这道题是动态规划和hashmap 的结合题。用hashmap 存储不重复字符及其出现的位置。dp[i] 表示以i 结尾的最长不含重复字符的子字符长度。i 位置的字符不在hashmap 中，动态转移方程：dp[i]=dp[i-1]+1,并将其加入到hashmap中，如果在i为的字符在hashmap 中，则获取其的位置pos。dp[i]=i-pos。 注意在第二种情况下，需要将hashmap进行清空。将pos到i 的位置的字符加入到hashmap中 。这是我在debug时候才发现的问题。

这道题也可以使用滑动窗口来做，也需要一个hashMap，这个hashmap 要记录不重复字符与其在字符串中的位置用来更新left。

代码实现：

public static int lengthOfLongestSubstring (String s) {

        //这个方法有问题
        int lens=s.length();
        if(lens<1){
            return 0;
        }
        //存储中间结果
        int[] dp = new int[lens];

        // 定义一个hashmap 存储不重复字符及其出现的位置
        HashMap<Character, Integer> hashmap = new HashMap<>();
        dp[0]=1;
        hashmap.put(s.charAt(0),0);

        for(int i=1;i<lens;i++){

            //hashmap 中没有
            if(!hashmap.containsKey(s.charAt(i))){
                hashmap.put(s.charAt(i),i);
                dp[i]=dp[i-1]+1;
            }else{
                // hashmap 中有, 获取位置
                int pos = hashmap.get(s.charAt(i));
                dp[i]=i-pos;
                //更新当前字符的位置
                //要将hashmap 中pos 到i 的char 放入hashmap 中 debug 时候才发现问题

                hashmap.clear();
                for(int j=pos+1;j<=i;j++){
                    hashmap.put(s.charAt(j),j);
                }
            }
        }
        int result=Integer.MIN_VALUE;
        for(int i=0;i<lens;i++){
            if(dp[i]>result){
                result=dp[i];
            }
        }
        return result;

    }

实现：

跳跃游戏二

思路：这道题也可以看作是一个区间类型的题。 dp[i]表示能否到达位置i，对每个位置i判断能否通过前面的位置跳跃过来，当前位置j能达到，并且当前位置j加上能到达的位置如果超过了i，那dp[i]更新为ture，便是i位置也可以到达。dp[i] 的计算需要中的结果。
假设能跳到最后一步，则 找能满足条件可以从 子问题中跳过来。先求其子问题。
复杂度：时间复杂度O(n^2)，空间复杂度O(n).

public boolean canJump(int[] nums) {
    int lens=nums.length;
    boolean [] dp=new boolean[lens];
    dp[0]=true;
    for(int i=1;i<lens;i++){
        for(int k=i-1;k>=0;k--){
            if(dp[k]==true && (i-k)<=nums[k]){
                dp[i]=true;
                break;
            }
        }
    }
    return dp[lens-1];
}

跳跃游戏

每个元素代表能跳跃的最大长度。

感觉需要使用动态规划，或贪心。

使用贪心，每次跳所能触及下标中的最大, 不光要考虑值，还要考虑距离。

动态规划: 最值型动态规划问题，dp[i]: 从第一个位置到该位置最短跳跃次数。初始值为数组的最大长度。

nums [2,3,1,1,4] dp[i]=min(dp[i],dp[j]+1) ( 0<=j<i && (i-j)<=nums[j] )
思考:

dp [0,1,1,2,2]
代码实现:

int lens=nums.length;
if(lens==0){
    return 0;
}
int [] dp=new int [lens];
dp[0]=0;
for(int i=1;i<lens;i++){
    dp[i]=10001;
    for(int j=0;j<i;j++){
        if(i-j<=nums[j]&& dp[i]==10001){
            dp[i]=Math.min(dp[i],dp[j]+1);
        }
    }
}
return dp[lens-1];

把数字翻译成字符串jz46

题目描述

解题思路： 属性: 个数，求最多。 这个题的状态表示和状态转移方程是我没有想到的
解密字符串就是将字符串划分成若干数字，每段数字对应一个字母。感觉这道题也可以通过回溯来做。

设字符串的长度为N，要求字符串前N 个字符的解密方式数，需要知道字符串前N-1 和N-2 个字符的解密方式数。 两者对应不同的字母，需要累加结果。

这道题是从后面进行分析的,两种情况: 整个数字的翻译结果数= 除去最后一位的部分翻译结果*1 （这里为什用乘是因为只会导致一种结果）整个数字的翻译结果= 除去最后两位的部分翻译结果 乘 1。 两者相加。 dp[i] 表示num[0,1,…i] 能够翻译成字符串的种类数。dp[i]=dp[i-1]+dp[i-2] 前提 10<=num[i-1,i]<=25。

代码实现

public static int translateNum(int num) {
    // 把int 转为字符串方便操作
    String s = String.valueOf(num);
    int lens=s.length();
    if(lens<1){
        return 0;
    }
    // dp[i] 表示以i 结尾能能翻译成的字符串的种类数
    int [] dp=new int[lens];
    // 初始化
    dp[0]=1;
    if(lens==1){
        return dp[0];
    }
    if(Integer.parseInt(s.substring(0,2))>=10 && Integer.parseInt(s.substring(0,2))<=25){
        dp[1]=2;
    }else{
        dp[1]=1;
    }

    for(int i=2;i<lens;i++){
        if(Integer.parseInt(s.substring(i-1,i+1))>=10 && Integer.parseInt(s.substring(i-1,i+1))<=25){
            dp[i]=dp[i-1]+dp[i-2];
        }else{
            dp[i]=dp[i-1];
        }
    }
    return dp[lens-1];
}

运行结果:

最大连续子序列和

问题描述：
输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。连续 i,i+1…

分析：求最大，考虑用动态规划，中间状态dp[i] 表示以第i 个元素结尾的最大连续自序列和。状态转移方程 dp[i]=Math.max(dp[i-1]+nums[i],nums[i]) 。最终结果为 dp[k](0<k<=n n为数组的个数）中的最大值。

public class 最大连续子序列和42 {
   public static void main(String[] args) {
       int [] nums={-2,1,-3,4,-1,2,1,-5,4};
       System.out.println(maxSubArray(nums));
   }
   public static int maxSubArray(int[] nums) {
       if (nums.length==0){
           return 0;
       }
       int [] dp=new int[nums.length];
       dp[0]=nums[0];
       for(int i=1;i<nums.length;i++){
           dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
       }
       int result=Integer.MIN_VALUE;
       for(int i=0;i<nums.length;i++){
           if(result<dp[i]){
               result=dp[i];
           }
       }
       return result;
   }

}

测试通过

连续子数组的最大和

题目描述：

解题思路：这一题与连续子数组的最大和一样，只不过不是求最大值而是将最大值的子数组进行返回。
这时候用到贪心，存储最大值的起始和结束的长度。本题我用了一个二维的数组。
代码实现

public static int[] FindGreatestSumOfSubArray (int[] array) {
        // write code here
        int lens=array.length;
        if(lens<0){
            return new int[]{};
        }
        //定义结构存储最终的结果
        int[] dp = new int[lens];
        //生成一个二维数组
        //存储起始和结束位置
        int [][] startEnd=new int[lens][2];
        dp[0]=array[0];
        startEnd[0][0]=0;
        startEnd[0][1]=0;
        for(int i=1;i<lens;i++){
            int value=dp[i-1]+array[i];
            if(value>=array[i]){
                startEnd[i][0]=startEnd[i-1][0];
                startEnd[i][1]=i;
                dp[i]=value;
            }else{
                startEnd[i][0]=i;
                startEnd[i][1]=i;
                dp[i]=array[i];
            }
        }

        int result=Integer.MIN_VALUE;
        int start=0,end=0;
        int spanFirst=0;
        for(int i=0;i<lens;i++){
            if(dp[i]>=result){
                if(dp[i]==result){
                    if(spanFirst<=(startEnd[i][1]-startEnd[i][0])){
                        start=startEnd[i][0];
                        end=startEnd[i][1];
                        spanFirst=end-start;
                    }
                }else{
                    start=startEnd[i][0];
                    end=startEnd[i][1];
                    spanFirst=end-start;
                }
                result=dp[i];
            }
        }
        //进行复制
        int span=end-start;
        int[] ints = new int[span+1];
        for(int i=0;i<span+1;i++){
            ints[i]=array[start];
            start++;
        }
        return ints;
    }

运行结果：

最长上升子序列

分析： 求最长考虑用动态规划，dp[i] 表示以i 结尾的最长递增子序列的长度，问题的解就是求解dp[0]…dp[n] (n为当前数组值减一)中的最大值。
状态转移dp[i]的计算也有两种情况，一种是当前数组A[i]的值大A[j] (j<i) ,那么dp[i]=dp[j]+1(因为j的值可能有多个，我们也要取dp[j]最大的)、第二种是A[i]都小于A[j] (j<i),那么以i 结尾的最长递增子序列只有A[i]一个元素。dp[i]=1。 所以状态转移方程就是
dp[i]=max(dp[j])+1 (j<i 并且A[i]>A[j]) dp[i]=1 (j<i并且 A[i]小于所有A[j])。

public static int lengthOfLIS(int[] nums) {
        if(nums.length==0){
            return 0;
        }
        int [] dp=new int[nums.length];
        dp[0]=1;
        Boolean flag=false;
        int result=Integer.MIN_VALUE;
        for(int i=1;i<nums.length;i++){
           for(int j=0;j<i;j++) {
               if(nums[i]>nums[j]){
                   int temp=dp[j]+1;
                   if(temp>dp[i]){
                       dp[i]=temp;
                   }
                   flag=true;
               }
           }
            //A[i] 都小于A[j] j 从0到i
            if(!flag){
                dp[i]=1;
            }
            // 重置flag
            flag=false;
        }

        for(int i=0;i<nums.length;i++){
            if(dp[i]>result){
                result=dp[i];
            }
        }
        return result;
    }

最长公共子序列

常规分析： 求最长用动态规划解决。状态表示：因为有两个字符串，设置两个变量i, j。假设dp[i,j]表示字符串A的i 号位和字符串B的j号位之前的最长公共子序列长度，那么最优解就是dp[n,m] n为字符串A的长度 m为字符串B的长度。为什么我们这次不以A字符串的i号位和B字符串的j号位结尾，如果以其结尾两个变量i,j我们就算求最优解的时间复杂度都是O(n^2)。状态转移dp[i,j] 计算有两种情况。第一种A[i]==B[j] 那么dp[i,j]=dp[i-1,j-1]+1 ，第二种A[i]!=B[j] 那么需要将i 增加 或者j 增加，取 max(dp[i-1],[j],dp[i][j-1 ] ).dp 使用二维数组。

代码

 public static int longestCommonSubsequence(String text1, String text2) {
        if(text1==null||text2==null){
            return 0;
        }
        int len1=text1.length();
        int len2=text2.length();
        int [][] dp=new int[len1+1][len2+1];
        //边界赋值为0 加1 是为了让边界全部设为0
        for(int i=0;i<len1+1;i++){
            dp[i][0]=0;
        }
        for(int i=0;i<len2+1;i++){
            dp[0][i]=0;
        }
        for(int i=1;i<len1+1;i++){
            for (int j=1;j<len2+1;j++){
                //这个二维数组的计算是一行一行的计算
                // 注意与矩阵连乘问题的区别
                if (text1.charAt(i-1)==text2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    // 从左边和上边边选元素
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[len1][len2];
    }

回文子串

题目描述

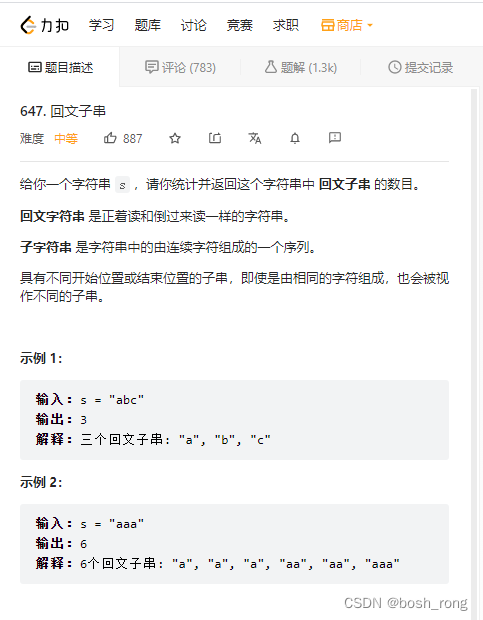
解题思路
// 回文子串个数，回溯也可以做，动态规划也可以做
// 动态规划 dp[i][j] 表示字符串 i 到j 是否为回文子串 i<j
// s[i]=s[j] j-i<=1 则为回文子串， s[i]=s[j] j-i>1 则需要判断 dp[i+1][j-1] 是否为回文子串,为回文子串为true，不是则返回false
// 状态转移方程为 dp[i][j]=(s[i][j] && dp[i+1][j-1])
// 左下角，从下往上填,从左往右填

public int countSubstrings(String s) {
        // 回文子串个数，回溯也可以做，动态规划也可以做
        // 动态规划 dp[i][j] 表示字符串 i 到j 是否为回文子串 i<j
        // s[i]=s[j] j-i<=1 则为回文子串， s[i]=s[j] j-i>1 则需要判断 dp[i+1][j-1] 是否为回文子串,为回文子串为true，不是则返回false
        // 状态转移方程为 dp[i][j]=(s[i][j] && dp[i+1][j-1])
        // 左下角，从下往上填,从左往右填
        int n= s.length();
        int ans =0;
        boolean [][] dp = new boolean[n][n];

        // i 列 从下到上
        for(int i=n-1;i>=0;i--){
            // j 行从左向右
            for(int j=i;j<n;j++){
                if((s.charAt(i)==s.charAt(j)) &&(j-i<=1 || dp[i+1][j-1])){
                    ans++;
                    dp[i][j] =true;
                }
            }
        }
        return ans;
    }

最长回文字串

题目描述

这里举最长回文子串的例子是为了与最长公共子序列做对比，主要是二维观察二维数组的生成过程。最长公共子序列的生成过程是一行一行生成。
解题分析：这道题可以使用暴力的方法的求解。暴力需要使用两个指针进行遍历，还需要一个for循环进行判断是否为回文串。所以其时间复杂度O（n^3)。
求最长使用动态规划进行尝试 。虽然这道题只给了一个字符串，但是在判断是否为回文的时候，涉及到一个区间,需要使用两个指针 dp[i,j] 表示子串 s[i…j ] 是否为回文子串。最优解就是求dp[i,j]为true时，i到j的最大值。状态转移方程 dp[i,j]=(s[i]==s[j]) && dp[i+1,j-1]。 边界 s[i,j]的长度为为2 和3的时候不需要判断子串是否为回文，只需要判断s[i]是否等于s[j]。初始状态dp[i,i]=0 。观察状态转移方程 dp[i,j]=(s[i]==s[j]) && dp[i+1,j-1], d[i,j]的计算要参考dp[i+1.j-1] 其在该值的的左下方，要保证左下方的值先计算出来。i与j 的关系是i 小于j ，只需填表的上半部分。

代码实现
暴力算法求解

 public String longestPalindrome(String s) {
        int lens=s.length();
        
        if(lens<2){
            return s;
        }
        // 记录最长回文串的开始位置和最长位置
        int maxLen=0;
        int begin=0;
        for(int i=0;i<lens-1;i++){
            for (int j=i;j<lens;j++){
                if(j-i+1>maxLen && checkPalindrome(s,i,j)){
                    maxLen=j-i+1;
                    begin=i;
                }
            }
        }
        return s.substring(begin,begin+maxLen);
    }
    public boolean checkPalindrome(String s,int begin,int end){
        while(begin<end){
            if(s.charAt(begin)!=s.charAt(end)){
                return false;
            }
            begin++;
            end--;
        }
        return true;
    }

动态规划求解

public   String longestPalindrome(String s) {
        int lens=s.length();
        if(lens<2){
            return s;
        }
        boolean [][] dp=new boolean[lens][lens];
        for(int i=0;i<lens;i++){
            dp[i][i]=true;
        }
        //默认最小为1个
        int maxLens=1;
        int begin=0;
        //先填列，再填行
        // i 右边界 j 左边界
        for(int j=1;j<lens;j++){
            for(int i=0;i<j;i++){
                if(s.charAt(i)==s.charAt(j) &&(j-i<3 || dp[i+1][j-1])){
                    dp[i][j]=true;
                    if(j-i+1>maxLens){
                        maxLens=j-i+1;
                        begin=i;

                    }
                }
                else {
                    dp[i][j]=false;
                }
            }

        }

        return s.substring(begin,begin+maxLens);
    }

动态规划解决二维路径问题

礼物的最大价值

题目描述：

状态表示 f[i] [j] 从起点走到(i,j) 能拿到的礼物价值的最大值。因为每次只能向右走或向下进行移动。状态转移方程: f[i][j]=Math.max(f[i][j-1],f[]i-1[j])+val(i,j)。 最终的结果为f[]m-1[n-1]。初始化第一行和第一列（累加初始化）。

代码实现：

public int maxValue (int[][] grid) {
        int rowLens=grid.length;
        int clomnLens=grid[0].length;

        int[][] dp=new int[rowLens][clomnLens];
        //状态转移方程 dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j])

        //初始化第一行和第一列
        int count=0;
        for(int i=0;i<clomnLens;i++){
            count+=grid[0][i];
            dp[0][i]=count;
        }
        count=0;
        for(int i=0;i<rowLens;i++){
            count+=grid[i][0];
            dp[i][0]=count;
        }


        for(int i=1;i<rowLens;i++){
            for(int j=1;j<clomnLens;j++){
                dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j])+grid[i][j];
            }
        }

        return dp[rowLens-1][clomnLens-1];
    }

01背包

状态表达: dp[i] [j] 选前i 个商品，现有体积为j（体积还剩j） 的最大价值。
状态转移方程: 第i 个商品不选，dp[i] [j]=dp[i-1] [j], 第i 个商品选: dp[i] [j] =dp[i-1] [j-wi]]+vi，两者选最大。
最终结果为 dp[i][V](i从1 到N) 中的最大值。

分析
若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1][v]；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。

代码实现:

public class 背包01 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int V = sc.nextInt();
        int[][] ints = new int[N+1][2];
        for(int i=1;i<=N;i++){
            // weights
            ints[i][0]=sc.nextInt();
            // values
            ints[i][1]=sc.nextInt();
        }

        int [][] dp=new int[N+1][V+1];
        for(int i=1;i<=N;i++){
            for(int j=0;j<=V;j++){
                dp[i][j]=dp[i-1][j];
                if(j>=ints[i][0]){
                    dp[i][j]=Math.max(dp[i][j],dp[i-1][j-ints[i][0]]+ints[i][1]);
                }
            }
        }
       
       System.out.println(dp[N][V]);

    }
}

递推方向:

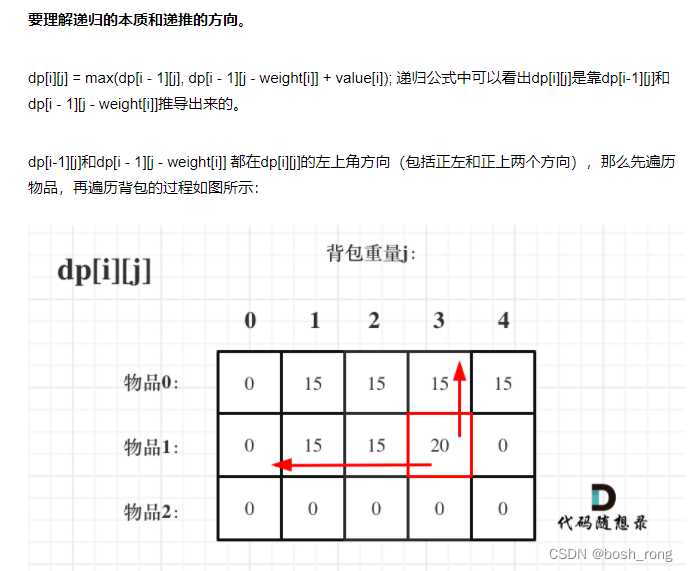
优化: dp【i】的状态只跟 dp[i-1]有关。
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

于其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。
一维dp数组遍历顺序。
dp[j]为 容量为j的背包所背的最大价值.。 不选容量不变，价值不变，选 dp[j - weight[i]] + value[i]
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
代码如下：

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
} 

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？ 倒叙遍历是为了保证物品i只被放入一次。

public class 背包01一维数组 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        // N个物品 V 背包容量
        int N = sc.nextInt();
        int V = sc.nextInt();
        int[][] ints = new int[N+1][2];
        for(int i=0;i<N;i++) {
            // weights
            ints[i][0] = sc.nextInt();
            // values
            ints[i][1] = sc.nextInt();
        }
        int [] dp = new int [V+1];
        dp[0] = 0;
        for(int i = 0; i<=N; i++){
            for(int j= V;j>=0;j--){
                if(j>=ints[i][0])
                    dp[j] = Math.max(dp[j], dp[j-ints[i][0]]+ ints[i][1]);
            }
        }
        System.out.println(dp[V]);
    }
}

分割等和子集

public class 分割等和子集 {
    public boolean canPartition(int[] nums) {
        // 分割等和子集 使用0 1 背包
        // 一维数组，从小到大遍历背包容量是完全背包
        // 从大到小是0 1 背包  dp[i] 剩余容量为i 的最大价值。
        // 如果 dp[total/2] = total/2 说明能划分为两个等和子集。,价值也是背包容量，最后判断total/2 容量的价值是否为total/2,是则可以分为2个等和子集。
        int total=0;
        int m = nums.length;
        for(int i=0;i<m;i++){
            total+=nums[i];
        }
        if(total%2!=0){
            return false;
        }
        total = total/2;

        int [] dp=new int[total+5];
        dp[0]=0;
        //先遍历物品，再遍历容量
        for(int i=0;i<m;i++){
            for(int j=total; j>=0;j--){
                // 背包容量大于当前啊物品
                if(j>=nums[i]){
                    dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
                }
            }
        }
        System.out.println(dp[total]);
        return dp[total]==total;
    }
}

目标和

题目描述

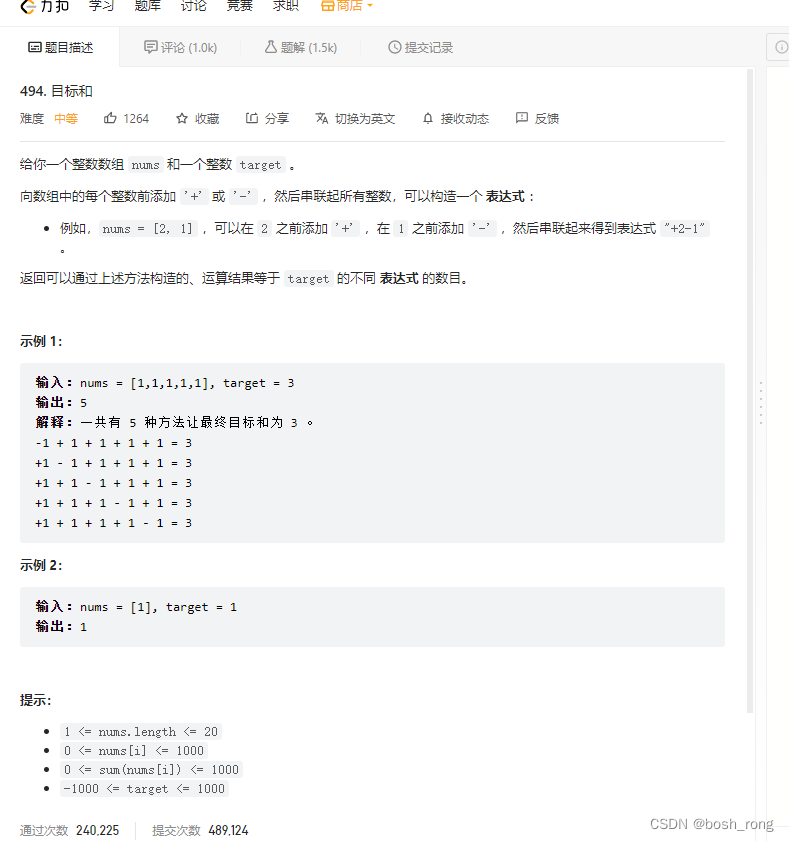
思路: 目标和 0 1 背包的思想
正数 总和 x ，负数总和 total -x 则 x -(total -x) = target 则 x=(total+target)/2 这与分割等和子集很像，但要求的是求个数。
dp[j]： 背包容量为i 所能构造的表达式数目 状态转移方程 dp[j] += dp[j-nums[i]]。

递推公式确定:

不考虑nums[i]的情况下，填满容量为j - nums[i]的背包，有dp[j - nums[i]]种方法。

那么只要搞到nums[i]的话，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]
已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]
已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 dp[5]
那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。
`

求装满背包有几种方法的情况下，递推公式一般为：dp[j] += dp[j - nums[i]]; 下面零钱兑换二 也是求个数。

     public int findTargetSumWays(int[] nums, int target) {
    // 思路:  目标和 0 1 背包的思想
    // 正数 总和 x  ，负数总和 total -x  则 x -(total -x) = target 则 x=(total+target)/2 这与分割等和子集很像，但要求的是求个数。
    // dp[j]： 背包容量为i 所能构造的表达式数目 状态转移方程  dp[j] += dp[j-nums[i]]
    // 求装满背包有几种方式，递推公式为 dp[]
    int n = nums.length;

    //dp[0] = 1 表示 target 为 0 一个数都不选
    int total = 0;
    for(int num : nums){
        total+=num;
    }
    if((total+target)%2!=0 || (total+ target)/2 <0){
        return 0;
    }
    target =(total + target) /2;
    int [] dp = new int[target+1];
    dp[0] = 1;
    for(int i = 0; i<n;i++){
        for(int j = target; j>=0;j--){
            if(j>=nums[i])
                dp[j] += dp[j-nums[i]];
        }
    }
    return dp[target];
} 

完全背包

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。
完全背包的物品是可以添加多次的，所以要从小到大去遍历背包容量。

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        // N个物品 V 背包容量
        int N = sc.nextInt();
        int V = sc.nextInt();
        int[][] ints = new int[N+1][2];
        for(int i=0;i<N;i++) {
            // weights
            ints[i][0] = sc.nextInt();
            // values
            ints[i][1] = sc.nextInt();
        }
        int [] dp = new int [V+1];
        dp[0] = 0;
        for(int i = 0; i<=N; i++){
            for(int j= 0;j<=V;j++){
                if(j>=ints[i][0])
                    dp[j] = Math.max(dp[j], dp[j-ints[i][0]]+ ints[i][1]);
            }
        }
        System.out.println(dp[V]);
    } 

零钱兑换二

题目描述:

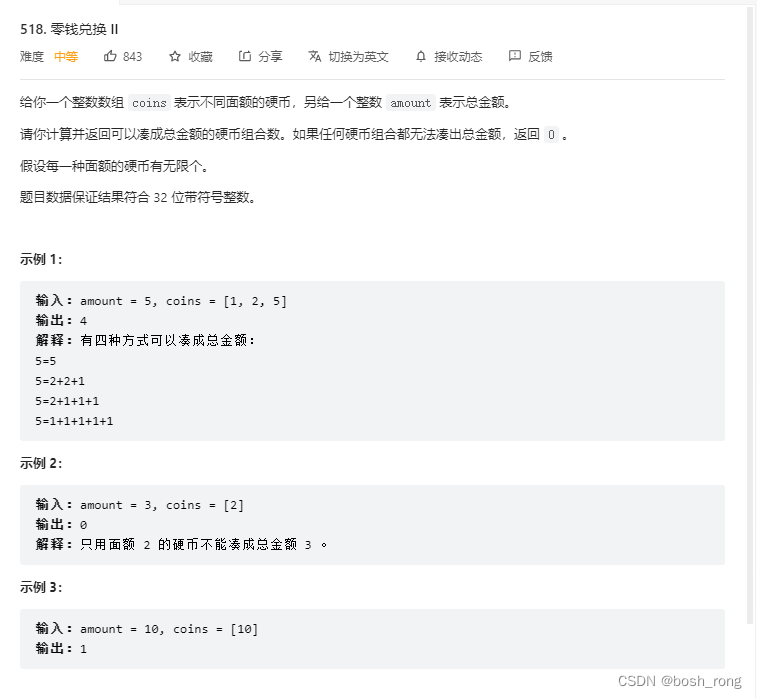
解题思路: 完全背包， dp[i] 表示 可以凑成总金额为 i 的硬币组合数。dp[i] += dp[i-coins[j]]。 dp[0] = 1 表示不凑,一种方案。

  public int change(int amount, int[] coins) {
        int n = coins.length;
        //dp[i] 表示 可以凑成总金额为 i 的硬币组合数
        // dp[i] += dp[i-coins[j]]
        // dp[0] = 1 表示不凑,一种方案
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= amount; j++) {
                if (j >= coins[i])
                    dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }

组合总和 Ⅳ

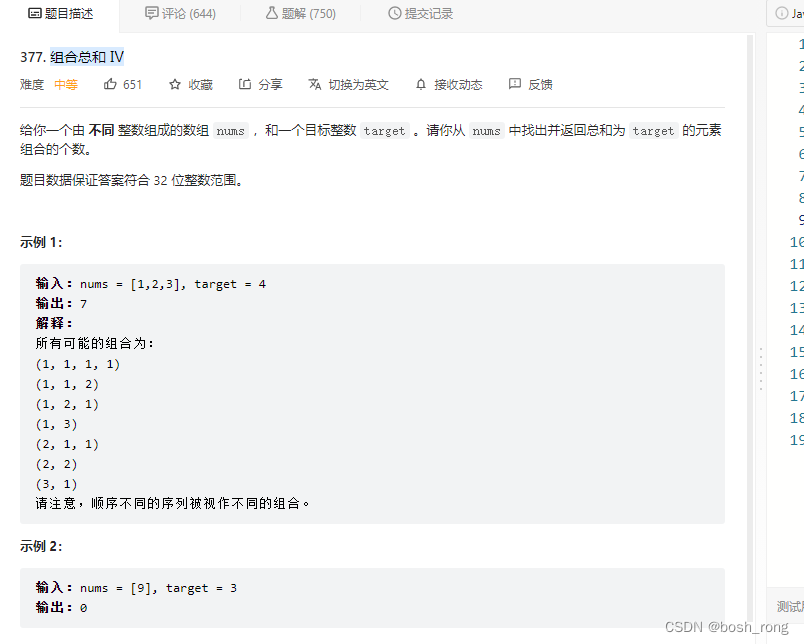
如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

 public int combinationSum4(int[] nums, int target) {
        // 这道题就是零钱总和二的变形,多了一个不同的顺序。
        // 回溯也可以做
        //如果求组合数就是外层for循环遍历物品，内层for遍历背包。
        // 如果求排列数就是外层for遍历背包，内层for循环遍历物品。
        int n = nums.length;
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < n; j++) {
                if (i >= nums[j])
                    dp[i] += dp[i - nums[j]];
            }
          
        }
        return dp[target];
    }

判断子序列

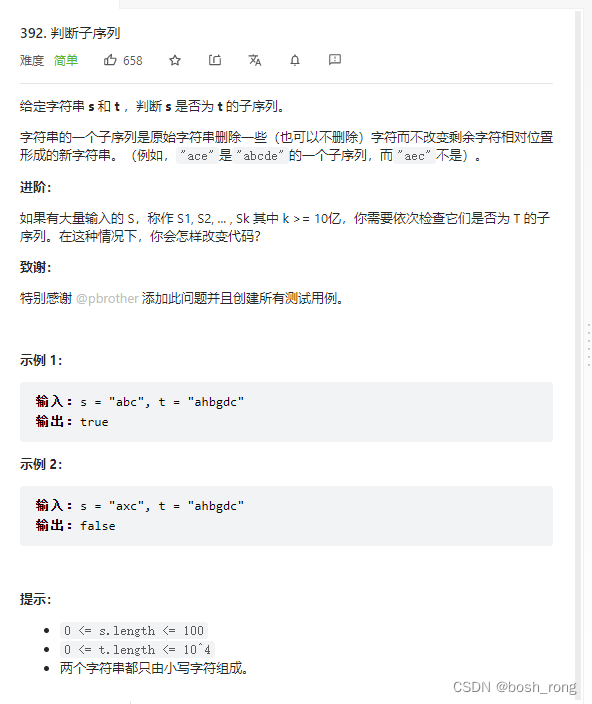
这道题是编辑距离的基础题，只涉及删除。
dp[i][j] 以i 结尾的字符串s 与j 结尾的字符串t,相同子序列的长度
如果s[i]=t[j] 则 dp[i][j] = dp[i-1][j-1] + 1
如果 s[i] != t[j] 则 dp[i][j] = dp[i][j-1] i不变，j 要依靠j-1 ， 相当于删除t 中j的位置。
最后判断 dp[m][n] 是否等于s 的长度，等于说明是子序列。

    public class 判断子序列 {
    public boolean isSubsequence(String s, String t) {
        // dp[i][j] 以i 结尾的字符串s 与j 结尾的字符串t,相同子序列的长度
        // 如果s[i]=t[j] 则 dp[i][j] = dp[i-1][j-1] + 1
        // 如果 s[i] != t[j] 则 dp[i][j] = dp[i][j-1] i不变，j 要依靠j-1 ， 相当于删除t 中j的位置。
        // 最后判断 dp[m][n] 是否等于s 的长度，等于说明是子序列
        int n = s.length();
        int m = t.length();
        int [][] dp= new int[n+1][m+1];
        for(int i=1;i<=n;i++){
            for(int j =1;j<=m;j++){
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[n][m]==s.length()-1;
    }
}

不同的子序列115

题目描述

解题思路:
// 动态规划，这一道题与编辑距离很相似。编辑距离有删除，替换，修改，这一题只有删除
// 判断子序列是用 s 去匹配t, 这道题使用 t 去匹配s ,删除的话i-1。
// dp[i][j] s 中以i 结尾的子序列，t在 中以j 结尾的的子序列中出现的个数
// 因为求的是个数，当s[i-1]==s[t-1] 时，有选或者不选s中i-1位置是否删除两个选择，将两个选择进行相加。
// s[i-1]==t[j-1] dp[i][j]=dp[i-1][j] 删除+ dp[i-1][j-1] 匹配
// s[i-1] !=t[j-1] dp[i][j] = dp[i-1][j]

public int numDistinct(String s, String t) {
        // 动态规划，这一道题与编辑距离很相似。编辑距离有删除，替换，修改，这一题只有删除
        // 判断子序列是用 s 去匹配t, 这道题使用 t 去匹配s ,删除的话i-1。
        // dp[i][j] s 中以i 结尾的子序列，t在 中以j 结尾的的子序列中出现的个数
        // 因为求的是个数，当s[i-1]==s[t-1] 时，有选或者不选s中i-1位置是否删除两个选择，将两个选择进行相加。
        // s[i-1]==t[j-1] dp[i][j]=dp[i-1][j] 删除+ dp[i-1][j-1] 匹配
        // s[i-1] !=t[j-1] dp[i][j] = dp[i-1][j]
        int n = s.length();
        int m = t.length();
        int [][] dp= new int [n+1][m+1];
        // dp[0][..] 初始化为 0 dp[i][0] 应该初始化为1 表示以s 中以i结尾的，全部删除，转化为t 中空串，其个数为1.

        for(int i=0;i<=n;i++){
            dp[i][0] = 1;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j] +dp[i-1][j-1];
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[n][m];
    }

两个字符串的删除

题目描述

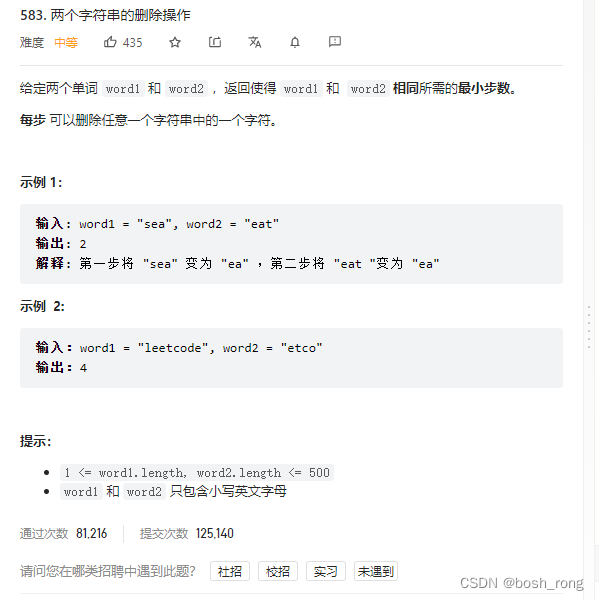
解题思路:

// 两个字符串都有操作
    // dp[i][j] word1 中以i 结尾，word2 中以j 结尾，相同的最小步数。
    // word1[i-1]= word2[j-1] dp[i][j] =dp[i-1][j-1] 无步数操作
    // word1[i-1] != word2[j-1]  dp[i][j] =min(dp[i-1][j]+1 删除word1 第i个位置,dp[i][j-1]+1,dp[i-1][j-1]+2)
    // 初始化 dp[i][0] 为i 表示word1 中删除几个元素才能变成空字符串 。dp[0][i]

public class 两个字符串的删除操作 {
    public int minDistance(String word1, String word2) {
        // 两个字符串都有操作
        // dp[i][j] word1 中以i 结尾，word2 中以j 结尾，相同的最小步数。
        // word1[i-1]= word2[j-1] dp[i][j] =dp[i-1][j-1] 无步数操作
        // word1[i-1] != word2[j-1]  dp[i][j] =min(dp[i-1][j]+1 删除word1 第i个位置,dp[i][j-1]+1,dp[i-1][j-1]+2)
        // 初始化 dp[i][0] 为i 表示word1 中删除几个元素才能变成空字符串 所以dp[i][0]初始化为i。同理dp[0][i]也初始化为i。
        int n = word1.length();
        int m = word2.length();
        int [][] dp= new int[n+1][m+1];
        for(int i =0;i<=n;i++){
            dp[i][0] = i;
        }
        for(int i=0;i<=m;i++){
            dp[0][i] =i;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(dp[i-1][j]+1,dp[i][j-1]+1);
                    dp[i][j] = Math.min(dp[i][j],dp[i-1][j-1]+2);
                }
            }
        }
        return dp[n][m];
    }
}

编辑距离

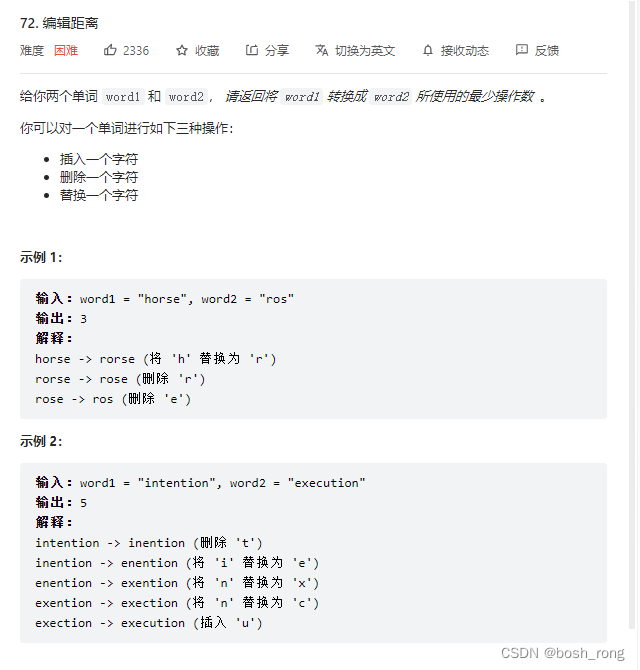
解题思路: 求最少的操作数，可以使用动态规划。dp[i][j] 表示把word1中 0~i的子串变为word 0到j 的子串的最小操作。
状态转移方程 word1[i] ==word2[j] 则dp[i][j]=dp[i-1][j-1]
否则 dp[i][j]=1+min(dp[i][j-1] 插入一个与j相同的，抵消一个j, dp[i-1][j] 删除，dp[i-1][j-1]) 替换

初始化时考虑的是 word1 和word2 中一个单词都没有的情况。与上面题一样初始化。
由状态转移方程可知，需要一行一行的填数据。

 public int minDistance(String word1, String word2) {
        public int minDistance(String word1, String word2) {
                int len1=word1.length();
                int len2=word2.length();
       int [][] dp=new int[len1+1][len2+1];
// 初始化
 for(int i=0;i<len1+1;i++){
    dp[i][0]=i;
  }
 for(int i=0;i<len2+1;i++){
    dp[0][i]=i;
}
for(int i=1;i<len1+1;i++){
   for(int j=1;j<len2+1;j++){
      if(word1.charAt(i-1)==word2.charAt(j-1)){
        dp[i][j]=dp[i-1][j-1];
    }else{
     int tmpMin=Math.min(dp[i-1][j],dp[i][j-1]);
     dp[i][j]=Math.min(tmpMin,dp[i-1][j-1])+1;
   }
  }
}
return dp[len1][len2];
}
    }

最长有效括号

题解：
// 最长有效括号
// dp[i] 表示从0~i 的字符串以s[i] 括号结尾能达到的最长括号子串的长度
// 如果当前是左括号，能否匹配要看后面的括号，可以忽略
// 如果当前是右括号，能否匹配要看前面的括号
// 如果 s[i]‘)’, s[i-1]=‘(’ dp[i] =2 要看s[i-2] 能否匹配
// s[i-2]‘(’ 匹配无法增长，如果s[i-2]‘)’ 为右括号，可以从dp 数组中的得到。 dp[i]+=dp[i-2]
// 2 当前为s[i] ）前一个也为s[i-1]== ) ，找已匹配之前的，根据dp[i]的值t， i-t-1 可知
// 如果 dp[i-t–1] 为 (, 能匹配 dp[i]=t+2，这时候还要看 dp[i-t-2] 是否为 ), 为) 则也要加上相应值。

 public int longestValidParentheses(String s) {
 int lens = s.length();
    if(lens<1){
        return 0;
    }
    int [] dp = new int [lens];
    for(int i=0;i<lens;i++){
        //情况一
        if( i>0 && s.charAt(i)==')'){
            if (s.charAt(i-1)=='('){
                dp[i]=2;
                if(i>=2 && s.charAt(i-2)==')'){
                    dp[i]+=dp[i-2];
                }
            }else if(s.charAt(i-1)==')'){
                int t = dp[i-1];
                // i-t 个已经匹配的
                if(i-t-1>=0 && s.charAt(i-t-1)=='('){
                    dp[i]=dp[i-1]+2;
                    if(i-t-2>=0 && s.charAt(i-t-2)==')'){
                        dp[i]+=dp[i-t-2];
                    }
                }
            }
        }
    }
    int res=-1;
    for(int i=0;i<lens;i++){
        if(dp[i]>res){
            res=dp[i];
        }
    }
    
    return res;
}

戳气球

题目描述

解题思路: 可以先拿一个气球，把这个气球当作最后一个气球，优先点爆左边和右边的气球之后，再点爆这个气球，可以看出左右两个子问题是独立的，它们只和这个气球有关联。

状态转移方程:
dp[i] [j] 表示 从第i 个气球到第j 个气球(闭空间)能够获取硬币的最大值。
则 dp[i][j] = dp[i][k-1] + dp[k+1][j] + nums[i-1]*nums[k] * nums[j+1] (i<=k<=j)

股票类型问题总结

具体可以看笔记

不同的二叉搜索树

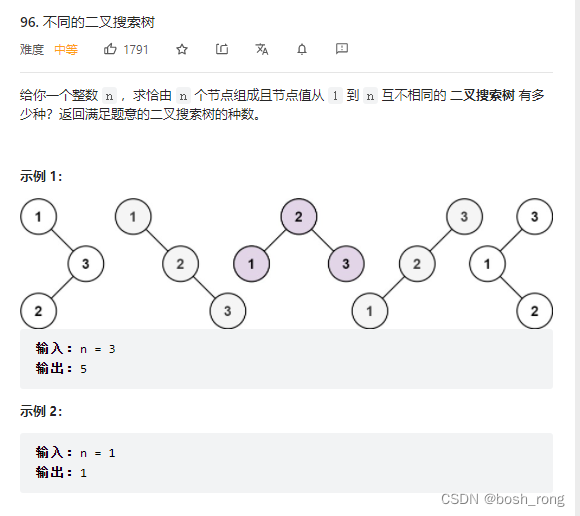
// dp[i] 从1 到i 互不相同的二叉搜索树个数,枚举1 到i，i个节点作为根节点的二叉树个数累加
// 假设选定的根节点是j ，
// dp[i]=(求和 j从1到i) dp(j-1) * dp(i-j);构造数量只与节点数有关。

public int numTrees(int n) {
        // dp[i] 从1 到i 互不相同的二叉搜索树个数,枚举1 到i，i个节点作为根节点的二叉树个数累加
        // 假设选定的根节点是j ，
        // dp[i]=(求和 j从1到i) dp(j-1) * dp(i-j);构造数量只与节点数有关。
        int [] dp= new int[n+1];
        dp[0] =1; // 要乘dp[0]=1
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[j-1]*dp[i-j];
            }
        } 
        return dp[n];
    }

不同的二叉搜索树二

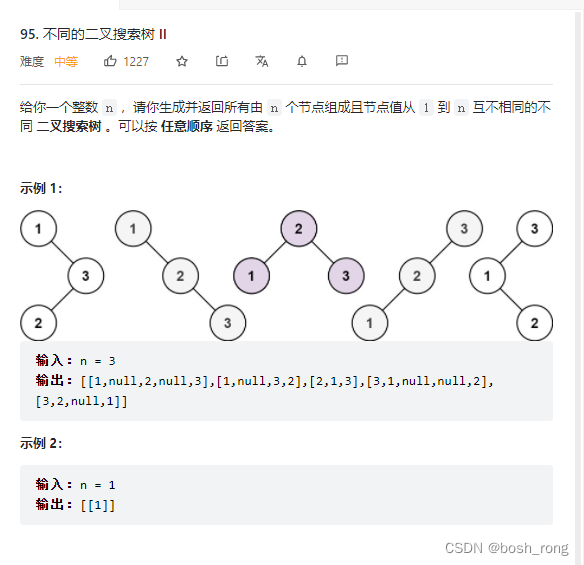
// 思想: 给定n ,以1~n 中某一个为根节点，则左孩子为左边遍历为左孩子（充当根节点），右孩子为右边遍历，为右孩子（充当根节点）
// 不断的去进行递归

 public static List<TreeNode> generateTrees(int n) {
        // 思想: 给定n ,以1~n 中某一个为根节点，则左孩子为左边遍历为左孩子（充当根节点），右孩子为右边遍历，为右孩子（充当根节点）
        // 不断的去进行递归
        if(n==0){
            return null;
        }
        return build(1,n);
    }

    // 要规定一个区间，左孩子和右孩子
    public static List<TreeNode> build(int s, int e){

        List<TreeNode> ans= new ArrayList<>();
        if(s > e){
            //返回空的集合
            ans.add(null);
            return ans;
        }
        //遍历这个区间的所有节点
        for(int i=s;i<=e;i++){
            //以i 为根节点去构造
            List<TreeNode> left = build(s,i-1);
            List<TreeNode> right = build(i+1,e);
            //遍历左边和右边
            for(TreeNode l : left){
                for(TreeNode r: right){
                    TreeNode newNode= new TreeNode(i);
                    newNode.left = l;
                    newNode.right = r;
                    ans.add(newNode);
                }
            }
        }
        return ans;
    }

（未完待续）