偏微分方程数值解法pdf_《常微分方程及其稳定性》（一）

点击返回目录

一. 基本知识

1.1 微分方程组

1.1.1 形式

一个动力学系统中存在许多随时间变化的变量（可以用向量来表示这个系统，向量中的元素就代表着不同的变量，如

），而这些变量之间往往又可能相互关联。因此，我们一般会采用一个微分方程组来描述这个动力学系统。

(1) 无依赖参数的微分方程组形式 （【1】P18的1.2.1和1.2.2式）（形式可参见【1】P51的例题1.2.12、P51的例1.2.13）

(2) 考虑依赖参数的微分方程组形式（【1】P19的1.2.4式）

1. 注意：
(1) 一定要切记每个

是个关于

变化的函数，即

，只是写的时候简记为

。因此微分方程组可以想象成很多条随着时间奔跑并舞动着的线条（也可能在转圈圈，路径没说是直线趋势哟）。

(2) 函数

可万万不能等价于我们要求解的结果，因为函数

还被许多变量

所决定着，而我们要求解的结果是只包含

的函数，即这些

。 微分方程组或许可以理解为一种“观测”结果，即各

之间表现出的关系，而我们要寻找的是其背后的决定性规律，即

。

1.1.2 Lipschitz条件

【1】P18的定义1.2.1。如果

在

上关于

具有一阶连续的偏导数，则它在

上关于

满足Lipschitz条件。

1. 理解：关于这个条件的理解，利普希茨连续的几何意义是什么？怎么较好的理解它呢？
说的很清楚。将定义改写为

会更清楚一些，这个公式告诉我们， 函数

中任意两点连线的斜率一致有界（即小于Lipschitz常数

），因此满足Lipschitz条件的连续函数比一般的连续函数更加光滑。此外，该条件还对函数

有两个额外的约束：(a) 函数

可导，则导数有界 （反过来，函数导数存在且有界，则可以推出该函数满足lipschitz条件）；(b) 要求 函数

在无限的区间上不能够有超过线性的增长（如

这些函数是不可以的）。

1.1.3 解的定理

(1) 解的存在唯一性定理（【1】P18的定理1.2.1）（总而言之，关键还是看微分方程组等式右边的函数

是否连续且满足Lipschitz条件）；

(2) 解的延拓定理（【1】P18的定理1.2.2）（即一根根线条从初始条件出发，随着

奔跑并舞动的过程，就是延拓）;

(3) 解对初值的连续依赖性和可微定理（【1】P18的定理1.2.3）（就是说，如果函数

连续且满足Lipschitz条件，则初值不同（但也离得很近很近）时，其解出来的线条簇也几乎是同样的情况，近乎可以重合）；

(4) 解对参数的连续性和可微性定理（【1】P19的定理1.2.4）（这个定理是针对考虑依赖参数的微分方程组的）。

1. 理解：都说Lipschitz条件在微分方程中特别重要，瞧瞧，就这里都已经很多定理是基于这个条件满足的基础上才能得到的啦。

1.2 微分、积分不等式

1.2.1 比较定理 （参见【1】P19的定理1.2.5）

1.2.2 Gronwall-Bellman不等式 （参见【1】P20的推论1.2.1，由P19的定理1.2.6得来）

1.2.3 第一比较定理 （参见【1】P20的定理1.2.7）

1.2.4 第二比较定理 （参见【1】P21的定理1.2.8）

1.3 微分方程的解析解法 （待更新）

1.4 微分方程的数值解法 （待更新）

二. 稳定性的基本定义

2.1 扰动运动的微分方程组

形式参见【1】P28的1.2.16式，推导参见【1】P27-28。说白了推导过程就是在进行问题的转换，即动力系统

如果是稳定的，则一定存在着系统的一个特解

，其对应的未被扰动是稳定的。那么啥时候这个特解是稳定的呢？这一步就要开始进行问题转换了，对它引入扰动变量

，得

。显然，如果它是稳定的，则扰动变量应该是稳定在零值。那么如何判断扰动变量是否稳定在零值呢？通过

【1】P28的1.2.16式上面的变换，我们就得到了关于扰动变量的微分方程组，即1.2.16式。最终，未被扰动运动

的稳定性就变为讨论关于这个新得到的扰动变量的微分方程组零解的稳定性了。这个新方程要

满足三个条件：(a) 连续； (b) 保证解存在唯一； (c)

。

Lyapunov稳定性的定义为：

称为系统的Lyapunov稳定平衡点，如果对任意运动轨迹

，只要初始状态离

很近，整个轨迹就不会远离平衡点

。具体到上面的问题，这个平衡点

就是零点啦，因为讨论的是零解的稳定性。

2.2 稳定性的相关概念定义

关于稳定性的相关概念定义参见【1】P28-29的定义。它们的关系划分如下图所示。这些概念看似大同小异，其实差别蛮大的，要注意区分不同。“渐近”意味着

时，

（这里讨论零解的稳定性），

“全局”意味着对任意的初始状态都成立，即不要求将初始状态限定在平衡点的一个邻接小范围内了， “一致”意味着与

中

的取值与

无关了（即每个时刻的情况都一致吧）。

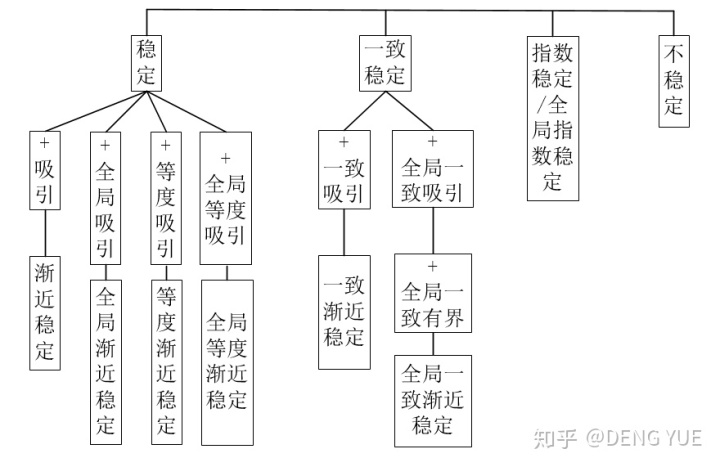
要理解它们，除了干瘪瘪的数学定义外，最好的方法就是从几何的角度进行理解。这里搬运几张老师课件上的图，整理如下图所示。

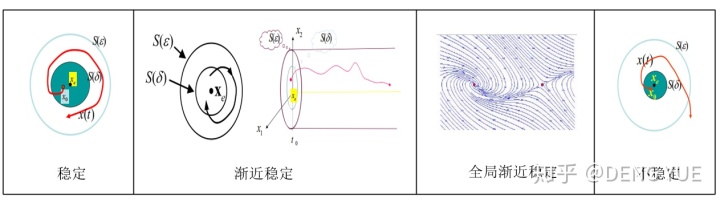
对于一些特殊的系统，包括：存在

而使得

的系统、

的自治系统、

的系统，上面的各种稳定性之间存在许多等价命题，即我们可以通过这些系统具有的一些稳定性特征，来互推出它们同时还具有另外的一些稳定性特征。具体参见

【1】P38-39的定理和推论。

点击返回目录