蒙特卡洛采样_蒙特卡洛马尔可夫链学习小结

目录

采样为什么是困难的(the curse of high dimensionality)

基于概率分布的采样Inverse Transform Sampling

接受-拒绝采样Rejection Sampling

MCMC 蒙特卡洛马尔可夫链

马氏链收敛到平稳分布的条件

可逆马尔科夫链蒙特卡洛RJMCMC简介

MCMC背景

在统计学中，经常会遇到高维积分的计算，用传统的数值方法往往很难解决高维积分计算问题。不过，通过随机模拟的方法为解决这些高维积分问题提供了一个思路。所谓随机模拟方法，是使通过随机变量函数的概率模拟或随机抽样求解工程技术问题的近似数值解的概率统计方法。

马尔可夫链蒙特卡洛MCMC，就是其中一种应用广泛的模拟方法，使得统计学领域中极大似然估计、非参数估计、贝叶斯统计学等方向上的很多问题得到了解决。

本次学习笔记参考了网络很多资源，就不列举了，这里推荐下，B站的 机器学习白板推导系列 。

关于采样的理解

什么是采样

所谓采样，简单来说就是按照某个概率分布(概率密度函数)，生成一批样本。比如下面按照均匀分布进行离散采样。假设离散变量r有3个取值，a1，a2，a3，概率分布如下图所示：

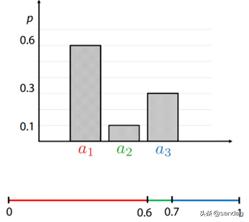
所有取值概率之和为1。此时我们可以从 Uniform[0,1) 生成一个随机数 b，若 0≤b<0.6，则选择出 a1；若 0.6≤b<0.7，则选择出 a2；若 0.7≤b<1，则选择出 a3。

为什么要采样

采样的动机通常有两种：

• 机器学习中，如果你已经通过训练学习出来一个模型，可能是个很复杂的概率分布函数。在推理阶段，需要从训练的概率分布中，产生一些样本。比如VAE、GAN生成模型中，输入一张图片到模型里，会生成一张新的图片，这个新生成的图片就是从概率分布中采样得到的。
• 简化对于复杂函数求和或求积分的运算，近似求解，比如蒙特卡洛积分。如果我们要计算上图中f(x)在[a, b]区域的面积。

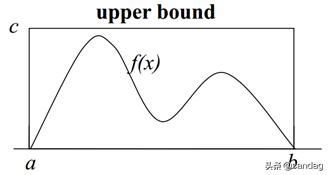
我们可以产生N个服从均匀分布的样本。然后统计处于函数f(x)曲线之下样本点的数量。这里就是采样的动机。

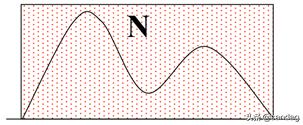
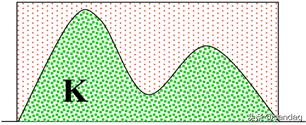
因此最终的面积为，

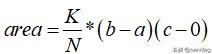
什么是好的样本

如果我们从P(x)分布中采集了N个样本，如何让这些样本点充分地表达P(x)？

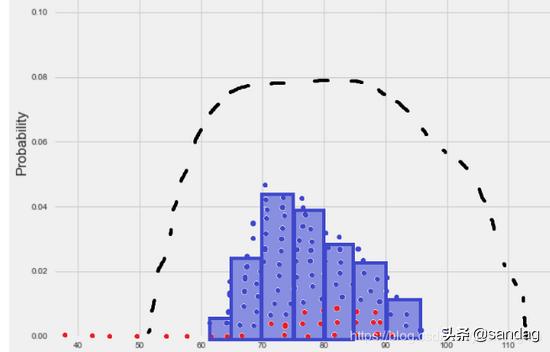
如上图所示，这些样本点应该大部分集中在高概率区域，概率越低的地方，样本点越稀疏。如果大部分样本点在低概率区域，那么这种采样就是失败的，无法表达当前分布。

如果上图表达了某国公民的财富的分布，虽说大部分人都是韭菜或者绵羊，但是从客观统计财富分布的情况，样本之间还是要有一定限制的，它们应该是相互独立的。比如，即使是收集了10个码农的存款数据，那么这10个码农也不要在同一家公司里，不然重复统计，相关性太强的样本，没有意义。

因此，好样本应该是，

(1)样本点趋向高概率区域，同时兼顾低概率区域。

(2)样本点之间相互独立

采样为什么是困难的(the curse of high dimensionality)

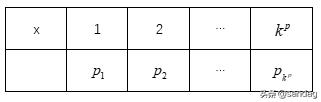
假设变量x是p维的，且每个维度有k种取值，即

，那么总的状态空间复杂度维

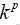
，且每个状态有自己的概率。为了使样本趋于高概率区域，不可能遍历每个状态的概率值，看看哪个高，哪个低。

蒙特卡洛采样方法

许多科学问题的基本部分都是计算下面形式的积分

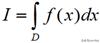
这里f(x)是感兴趣的目标函数，D通常是高维空间种的一个区域。通常情况下，如果问题稍微复杂一点，这个积分就难以计算。但是根据数学期望的定理，我们可以另辟蹊径。

若随机变量Y符合函数

，

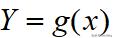
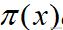
为概率密度函数，且

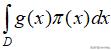
绝对收敛，则有：

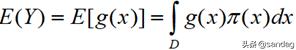
根据上述定理，如果f(x)可以被分解成一个函数g(x)与一个概率密度函数f(x)的乘积，那么上述f(x)积分可以看作是g(x)在密度

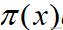
下的期望。另外，我们求E(Y)时不需要算出Y的概率分布，只要利用X的概率密度即可。

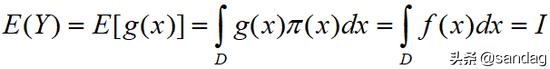
这样，如果我们能得到

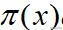
的独立样本