微信公众号:医学统计与R语言
Code
√输入1:
install.packages("rio")
library(rio)
qol1 import("qol.sav")
linqol data=qol1)
summary(linqol)
√结果1:
Call:
lm(formula = 生理功能 ~ newincome + Q34 + newQ35 + Q36, data = qol1)
Residuals:
Min 1Q Median 3Q Max
-41.130 -9.744 -0.272 10.653 27.853
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 89.5463 2.7487 32.577 2e-16 ***
newincome 2.6830 0.6792 3.950 8.61e-05 ***
Q34 2.0889 0.9786 2.135 0.0331 *
newQ35 -9.5109 0.9972 -9.538 2e-16 ***
Q36 -1.5746 1.1292 -1.394 0.1636
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.68 on 688 degrees of freedom
Multiple R-squared: 0.1701, Adjusted R-squared: 0.1653
F-statistic: 35.26 on 4 and 688 DF, p-value: 2.2e-16
√输入2:
coefficients(linqol) # model coefficients
confint(linqol, level=0.95) # CIs for model parameters
fitted(linqol) # predicted values
residuals(linqol) # residuals
anova(linqol) # anova table
vcov(linqol) # covariance matrix for model parameters
influence(linqol) # regression diagnostics
√输入3:
install.packages("lm.beta")
library(lm.beta)
stlm <- lm.beta(linqol)
summary(stlm)
√结果3:
Call:
lm(formula = 生理功能 ~ newincome + Q34 + newQ35 + Q36, data = qol1)
Residuals:
Min 1Q Median 3Q Max
-41.130 -9.744 -0.272 10.653 27.853
Coefficients:
Estimate Standardized Std. Error t value Pr(>|t|)
(Intercept) 89.54626 0.00000 2.74875 32.577 2e-16 ***
newincome 2.68304 0.14019 0.67918 3.950 8.61e-05 ***
Q34 2.08892 0.07442 0.97857 2.135 0.0331 *
newQ35 -9.51092 -0.34045 0.99719 -9.538 2e-16 ***
Q36 -1.57462 -0.04968 1.12919 -1.394 0.1636
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.68 on 688 degrees of freedom
Multiple R-squared: 0.1701, Adjusted R-squared: 0.1653
F-statistic: 35.26 on 4 and 688 DF, p-value: 2.2e-16
√输入4:
install.packages("MASS")
library(MASS)
step "both")
√结果4:
Start: AIC=3525.82
生理功能 ~ newincome + Q34 + newQ35 + Q36
Df Sum of Sq RSS AIC
- Q36 1 312.8 110990 3525.8
110677 3525.8- Q34 1 733.0 111410 3528.4- newincome 1 2510.5 113187 3539.4- newQ35 1 14633.7 125310 3609.9
Step: AIC=3525.78
生理功能 ~ newincome + Q34 + newQ35
Df Sum of Sq RSS AIC 110990 3525.8+ Q36 1 312.8 110677 3525.8- Q34 1 730.4 111720 3528.3- newincome 1 2754.7 113744 3540.8- newQ35 1 15874.9 126864 3616.4√输入5:
step$anova
√结果5:
Stepwise Model Path
Analysis of Deviance Table
Initial Model:
生理功能 ~ newincome + Q34 + newQ35 + Q36
Final Model:
生理功能 ~ newincome + Q34 + newQ35
Step Df Deviance Resid. Df Resid. Dev AIC
1 688 110676.8 3525.824
2 - Q36 1 312.8098 689 110989.6 3525.780
√输入6:
install.packages("olsrr")
library(olsrr)
ols_step_best_subset(linqol)
olsrr:Tools for Building OLS Regression Models
√结果6:
Best Subsets Regression
---------------------------------------
Model Index Predictors
---------------------------------------
1 newQ35
2 newincome newQ35
3 newincome Q34 newQ35
4 newincome Q34 newQ35 Q36
---------------------------------------
Subsets Regression Summary
---------------------------------------------------------------------------------------------------------------------------------------
Adj. Pred
Model R-Square R-Square R-Square C(p) AIC SBIC SBC MSEP FPE HSP APC
---------------------------------------------------------------------------------------------------------------------------------------
1 0.1398 0.1385 0.1348 24.1685 5513.3715 3546.6080 5526.9946 166.5088 166.5074 0.2406 0.8652
2 0.1623 0.1599 0.155 7.4850 5496.9744 3530.3127 5515.1385 162.6173 162.6139 0.2350 0.8450
3 0.1678 0.1641 0.1581 4.9445 5494.4287 3527.8153 5517.1338 162.0238 162.0177 0.2341 0.8419
4 0.1701 0.1653 0.158 5.0000 5494.4728 3527.8966 5521.7190 162.0375 162.0280 0.2342 0.8420
---------------------------------------------------------------------------------------------------------------------------------------
AIC: Akaike Information Criteria
SBIC: Sawa's Bayesian Information Criteria
SBC: Schwarz Bayesian Criteria
MSEP: Estimated error of prediction, assuming multivariate normality
FPE: Final Prediction Error
HSP: Hocking's Sp
APC: Amemiya Prediction Criteria
√输入7:
ols_step_forward_p(linqol)
√结果7:
Variables Entered:
✔ newQ35
✔ newincome
✔ Q34
✔ Q36
Final Model Output
------------------
Model Summary
---------------------------------------------------------------
R 0.412 RMSE 12.683
R-Squared 0.170 Coef. Var 15.567
Adj. R-Squared 0.165 MSE 160.867
Pred R-Squared 0.158 MAE 10.589
---------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
ANOVA
-----------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
-----------------------------------------------------------------------
Regression 22686.456 4 5671.614 35.256 0.0000
Residual 110676.752 688 160.867
Total 133363.208 692
-----------------------------------------------------------------------
Parameter Estimates
-----------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-----------------------------------------------------------------------------------------
(Intercept) 89.546 2.749 32.577 0.000 84.149 94.943
newQ35 -9.511 0.997 -0.340 -9.538 0.000 -11.469 -7.553
newincome 2.683 0.679 0.140 3.950 0.000 1.350 4.017
Q34 2.089 0.979 0.074 2.135 0.033 0.168 4.010
Q36 -1.575 1.129 -0.050 -1.394 0.164 -3.792 0.642
-----------------------------------------------------------------------------------------
Selection Summary
----------------------------------------------------------------------------
Variable Adj.
Step Entered R-Square R-Square C(p) AIC RMSE
----------------------------------------------------------------------------
1 newQ35 0.1398 0.1385 24.1685 5513.3715 12.8852
2 newincome 0.1623 0.1599 7.4850 5496.9744 12.7245
3 Q34 0.1678 0.1641 4.9445 5494.4287 12.6920
4 Q36 0.1701 0.1653 5.0000 5494.4728 12.6834
----------------------------------------------------------------------------
√输入8:
ols_step_backward_p(linqol)
√结果8:
Backward Elimination Method
---------------------------
Candidate Terms:
1 . newincome
2 . Q34
3 . newQ35
4 . Q36
We are eliminating variables based on p value...
Variables Removed:
No more variables satisfy the condition of p value = 0.3
Final Model Output
------------------
Model Summary
---------------------------------------------------------------
R 0.412 RMSE 12.683
R-Squared 0.170 Coef. Var 15.567
Adj. R-Squared 0.165 MSE 160.867
Pred R-Squared 0.158 MAE 10.589
---------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
ANOVA
-----------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
-----------------------------------------------------------------------
Regression 22686.456 4 5671.614 35.256 0.0000
Residual 110676.752 688 160.867
Total 133363.208 692
-----------------------------------------------------------------------
Parameter Estimates
-----------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-----------------------------------------------------------------------------------------
(Intercept) 89.546 2.749 32.577 0.000 84.149 94.943
newincome 2.683 0.679 0.140 3.950 0.000 1.350 4.017
Q34 2.089 0.979 0.074 2.135 0.033 0.168 4.010
newQ35 -9.511 0.997 -0.340 -9.538 0.000 -11.469 -7.553
Q36 -1.575 1.129 -0.050 -1.394 0.164 -3.792 0.642
-----------------------------------------------------------------------------------------
[1] "No variables have been removed from the model."
√输入9:
ols_step_both_p(linqol)
√结果9:
Stepwise Selection Method
---------------------------
Candidate Terms:
1. newincome
2. Q34
3. newQ35
4. Q36
We are selecting variables based on p value...
Variables Entered/Removed:
✔ newQ35
✔ newincome
✔ Q34
No more variables to be added/removed.
Final Model Output
------------------
Model Summary
---------------------------------------------------------------
R 0.410 RMSE 12.692
R-Squared 0.168 Coef. Var 15.578
Adj. R-Squared 0.164 MSE 161.088
Pred R-Squared 0.158 MAE 10.627
---------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
ANOVA
-----------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
-----------------------------------------------------------------------
Regression 22373.647 3 7457.882 46.297 0.0000
Residual 110989.561 689 161.088
Total 133363.208 692
-----------------------------------------------------------------------
Parameter Estimates
-----------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-----------------------------------------------------------------------------------------
(Intercept) 87.732 2.423 36.208 0.000 82.975 92.489
newQ35 -9.754 0.983 -0.349 -9.927 0.000 -11.683 -7.825
newincome 2.792 0.675 0.146 4.135 0.000 1.466 4.117
Q34 2.085 0.979 0.074 2.129 0.034 0.163 4.008
-----------------------------------------------------------------------------------------
Stepwise Selection Summary
----------------------------------------------------------------------------------------
Added/ Adj.
Step Variable Removed R-Square R-Square C(p) AIC RMSE
----------------------------------------------------------------------------------------
1 newQ35 addition 0.140 0.139 24.1680 5513.3715 12.8852
2 newincome addition 0.162 0.160 7.4850 5496.9744 12.7245
3 Q34 addition 0.168 0.164 4.9450 5494.4287 12.6920
----------------------------------------------------------------------------------------
√输入10:
library(leaps)
leaps<-regsubsets(生理功能~newincome+ Q34 +newQ35+ Q36,data=qol1)summary(leaps)leaps() performs an exhaustive search for the best subsets of the variables in x for predicting y in linear regression, using an efficient branch-and-bound algorithm
√结果10:
Subset selection object
Call: regsubsets.formula(生理功能 ~ newincome + Q34 + newQ35 + Q36,
data = qol1)
4 Variables (and intercept)
Forced in Forced out
newincome FALSE FALSE
Q34 FALSE FALSE
newQ35 FALSE FALSE
Q36 FALSE FALSE
1 subsets of each size up to 4
Selection Algorithm: exhaustive
newincome Q34 newQ35 Q36
1 ( 1 ) " " " " "*" " "
2 ( 1 ) "*" " " "*" " "
3 ( 1 ) "*" "*" "*" " "
4 ( 1 ) "*" "*" "*" "*"
An asterisk indicates that a given variable is included in the corresponding model.
√输入11:
plot(leaps, scale = "adjr2", main = "Adjusted R^2")
√结果11:
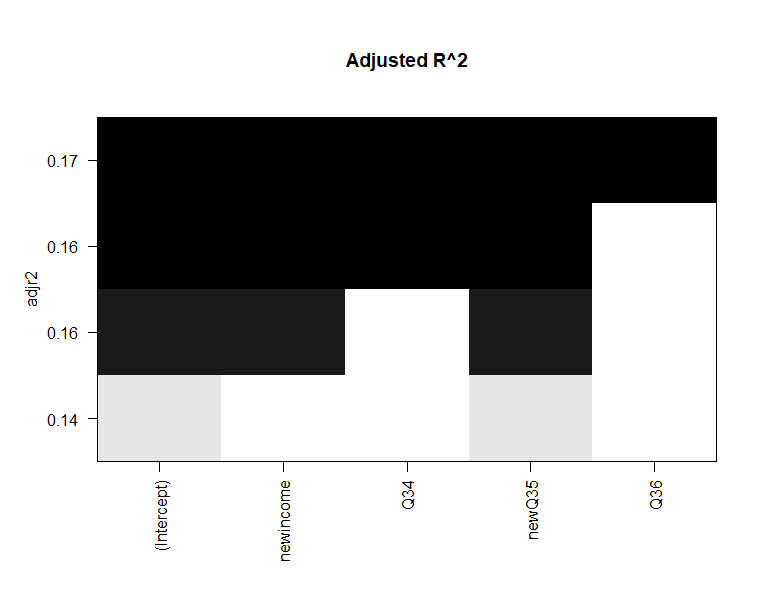
√输入12:
plot(leaps, scale = "bic", main = "BIC")
√结果12:
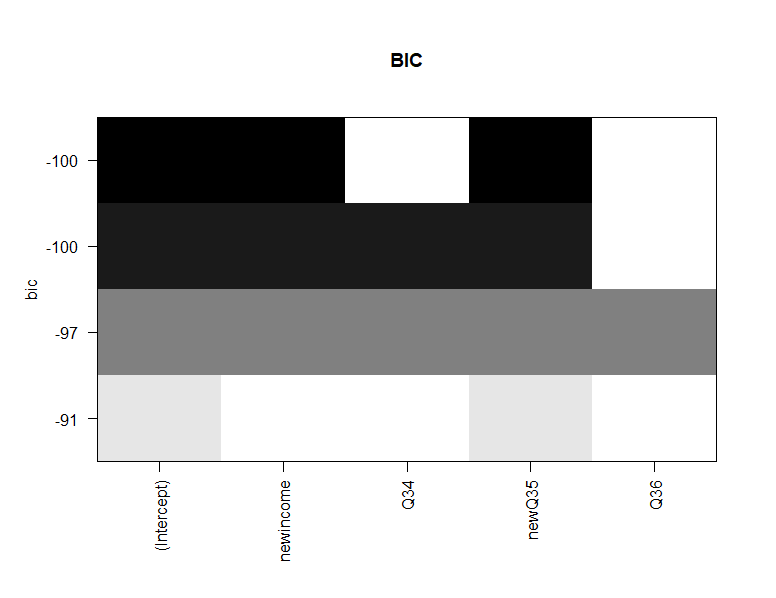
√输入13:
install.packages("car")
library(car)
subsets(leaps, statistic="adjr2", main = "Adjusted R^2")
√结果13:
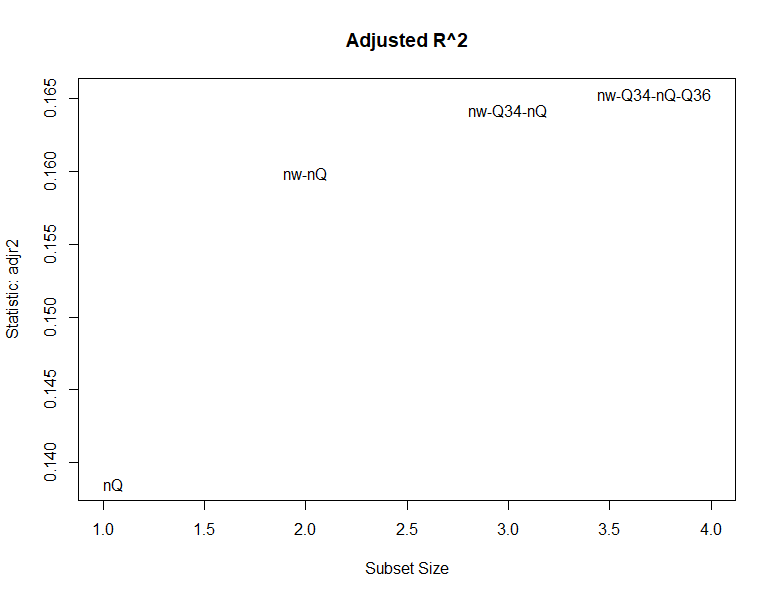





 本文介绍了在R语言中进行多重线性回归分析时,如何选择最佳自变量的多种方法,包括使用olsrr包和leaps包进行模型构建和变量筛选。详细展示了从输入代码到得到结果的步骤,提供了清晰的操作示例。
本文介绍了在R语言中进行多重线性回归分析时,如何选择最佳自变量的多种方法,包括使用olsrr包和leaps包进行模型构建和变量筛选。详细展示了从输入代码到得到结果的步骤,提供了清晰的操作示例。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








