求两条轨迹间的hausdorff距离_【每周三题】高二【136】分子间作用力和分子势能...

【题头】

   人们对问题的研究是逐步从对宏观物体的研究发展到对微观领域研究的。分子动理论的内容是分析微观分子间的相互作用，并通过动力学、能量的方法对微观问题进行分析。

---

【例题】

分子力F、分子势能E_P与分子间距离r的关系图线如甲乙两条曲线所示(取无穷远处分子势能E_P=0).下列说法正确的是

A．乙图线为分子势能与分子间距离的关系图线

B．当r=r₀时，分子势能为零

C．随着分子间距离的增大，分子力先减小后一直增大

D．分子间的斥力和引力大小都随分子间距离的增大而减小，但斥力减小得更快

E. 在r<r₀阶段，分子力减小时，分子势能也一定减小

【解析】

A、B项：在r＝r₀时，分子势能最小，但不为零，此时分子力为零，故A项正确，B项错误；

C项：如图甲所示，分子间作用力随分子间距离增大先减小，然后反向增大后又减小，C项错误；

D项：分子间的引力和斥力都随分子间距离的增大而减小，随分子间距离的减小而增大，但斥力比引力变化得快，D项正确；

E项：当r＜r₀时，分子力表现为斥力，当分子力减小时，分子间距离增大，分子力做正功，分子势能减少，E项正确。

故选ADE。

---

【拓展】

如图甲所示，a、b为某种物质的两个分子，假设分子a固定不动，分子b只在ab间分子力的作用下运动(在x轴上)，以a为原点，沿两分子连线建立x轴。两个分子之间的作用力与它们之间距离x的F−x关系图线如图乙所示。图线在r₀处的斜率为k，当分子b在两分子间距r₀附近小范围振动时：

(1)弹簧、橡皮筋等弹性物质大多有“弹性限度”，在“弹性限度”范围遵守胡克定律，请结合图乙从微观尺度上谈谈你对“弹性限度”范围的理解。说明在“弹性限度”范围内，微观层面上分子b的运动形式；

(2)推导两分子间距为x(x≥r₀)时，两分子间分子势能E_P的表达式；当两分子间距离为r₀时，b分子的动能为E_k0。求两分子在r₀附近小范围振动时的振动范围。当温度小范围升高时，热运动加剧，A同学认为分子振动范围变大，频率不变；B同学认为分子振动频率变大。哪位同学的观点正确？

【解析】

(1)弹力是分子力的宏观表现，从微观尺度上看，只有在r₀附近，分子力才和分子偏离r₀的距离成正比，宏观上表现为“弹性限度”范围。在“弹性限度”范围内，微观层面上分子b的运动形式是简谐运动。

(2)在F−x图中，当x≥r₀时图线与x轴所围成的面积表示弹力F做的功，则在位移从r₀变为x的过程中，弹力做功为

所以弹性势能为

当两分子间距离为r₀时，b分子的动能为E_k0，以此位置为起点，当b分子的动能全部转化为分子势能时即为最远点，所以有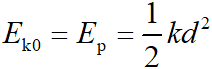，可得

根据简谐振动的对称性可知振动范围为

当温度小范围升高时，热运动加剧，E_k0增大，则振动范围增大，但r₀附近的斜率不变，故频率不变，故A同学正确。

【品析】

由以上分析我们可以看到，在分析分子动理论问题时，我们需要将分子力与分子间距离的关系分析清楚，并注意所分析的过程中分子力大小的变化及分子力做功的情况，从而判断分子的运动情况及分子势能变化的情况。同时我们还需要将有关分子力的分子模型与其它力学模型对比分析，并利用其它力学模型分析问题。

---

【作者简介】

   王巨生，北京市第八十中学物理教师，朝阳区物理学科带头人，中学高级教师。

---

欢迎投稿

邮箱：wlxxyjtg@126.com(物理学习研究投稿首字母)

具体要求请看“物理学习研究”公众号“交流合作”下的“关于我们”或者在公众号直接回复 投稿 二字，我们将具体要求直接回复给您！

---

审核：张春丽、石亚璞   

编辑：石明