d3力导向图增加节点_【钢结构·技术】 桁架的节点为什么可以看作铰接？

桁架是一种普遍应用的杆系结构。图7与图8就是桁架结构桥梁。所谓桁架，就是杆系结构中的每一根杆都是结构中几何单形的一条边，对于平面桁架，单形就是三角形，每一根杆都至少是一个三角形的一条边，对于空间桁架，单形就是四面体，每一根杆都至少是一个四面体的一个棱。所以如果把桁架的每一根杆都看作刚体，它们所构成的杆系是不会变形的，是十分坚固的。

桁架的历史是久远的。古罗马时代的建筑师维特鲁威(Marcus Vitruvius Pollio，生于80-70BC，逝世于15BC)所著《建筑十书》中所介绍的起重机械(图1)和攻击机械郝格托尔撞锤和龟(图2)的结构可以看作最早的桁架。桁架在建造木桥和屋架上最先见诸实用(图3)。古罗马人用桁架修建横跨多瑙河的特雷江桥的上部结构(发现于罗马的浮雕中)，文艺复兴时期，意大利建筑师帕拉迪奥(Andrea Palladio，1508—1580)开始采用木桁架建桥，后来出现了华伦式、汤式、豪式等不同形式的桁架(图4-6)。19世纪五十年代之后才出现钢结构桁架。

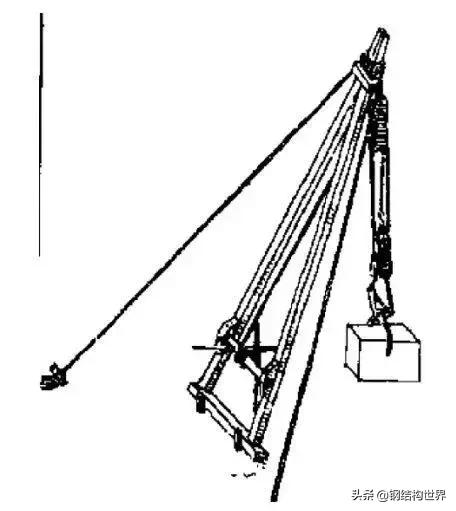
图1 《建筑十书》中介绍的起重装置

图2 郝格托尔撞锤和龟

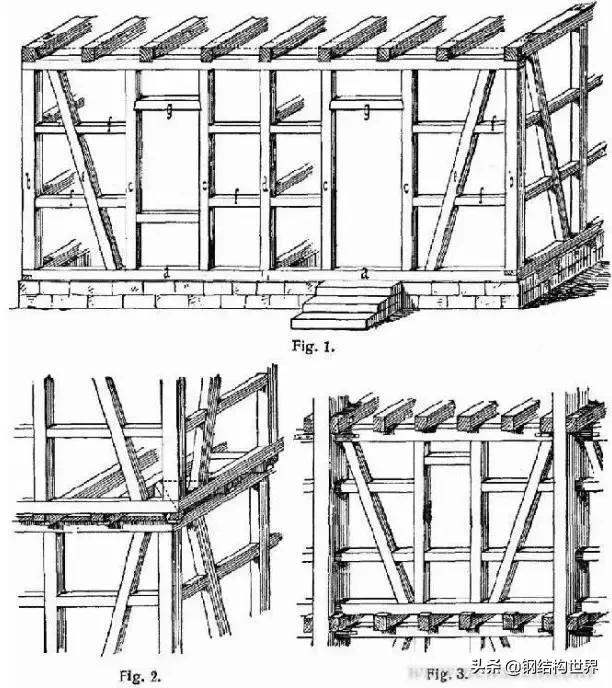
图3 古罗马时代早期木结构桁架

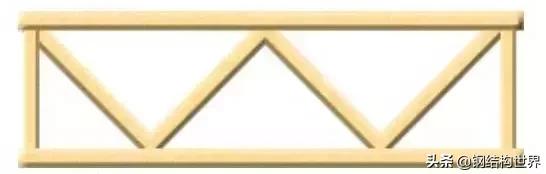
图4 华伦式桁架(James Warren 1848获英国专利)

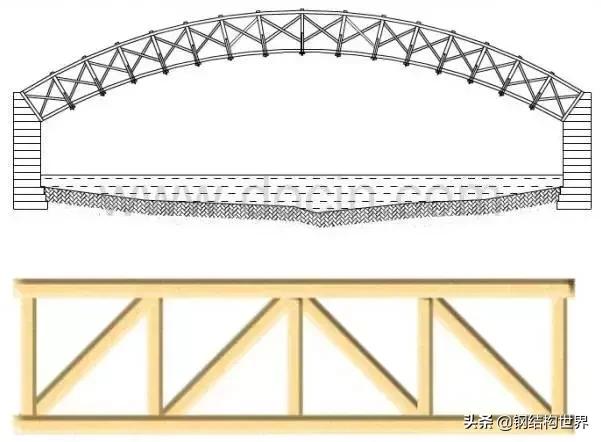
图5 豪式(William Hawe 1840年设计并获专利)桁架，增加了竖直杆

图6 汤式网格(Ithiel Town 于1820年获英国专利)桁架

图7 1924年建成的上海浙江路桁架结构桥

图8 施工过程中的桁架桥梁

结构力学在分析桁架的各个杆的受力时，需要简化。归结起来就两条：

• 一条是所有的外力作用在桁架的节点上；
• 一条是桁架的所有节点都是铰接的，也就是说每一根杆可以绕节点自由转动。

这两条的实质是，桁架的每一根杆只受拉压力，不受弯矩的作用，亦即没有弯曲。

我们注意图7、图8的桁架，前一个桁架的节点是铆接的，后一个节点是焊接的，都是固接，杆与杆之间并不能相互转动。为什么在做分析的时候却能把这些节点简化为铰接的呢？这需要仔细说说。就是说，我需要估算在桁架的杆件变形时，杆件所受的弯曲程度。如果我们能够证明在任何情况下，杆件弯曲所引起的应力比拉压的应力都小许多，那么我们当然就可以略去杆件的弯曲，把桁架的节点看做铰接了。

不妨设杆的长度为l，杆的截面尺寸为a，并且a<<l，即截面尺寸比长度小一个数量级。现在我们设杆系中有一根杆受拉(或压)力，力的大小为杆的比例极限，这是在设计时，杆能够承受的比较大的力了，因为大过它，材料就会受到不可恢复的塑性变形。一般在碳钢的情形，它相当于杆伸长(或压缩)了原长的千分之一，即l/1000。还设这根杆的一端是固定的，于是另一端就移动了l/1000，于是在这一段相联接的另一根杆便产生了横向的位移。不妨假定它的横向位移就是l/1000(其实只有在另一根杆与变形的杆相互垂直时才是这样的，一般情形，横向位移要小)。

我来讨论，这另一根一端横向位移为l/1000，一端固定的杆的弯曲变形。这是一根悬臂梁。设它在固定端所受的弯矩为M，则由材料力学简单的计算可以达到位移端的横向位移应当是：

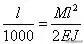
这里E是材料的杨氏模量，J是截面的转动惯量。由这个式子可以求出杆固定端的弯矩M，从而得到那里最大的弯曲应力

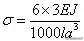
考虑到J=a⁴/12于是上式就化为

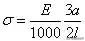
我们既然知道受拉杆的变形是l/1000，它的应变是1/1000，所以拉压应力是E/1000，现在弯曲应力多出一个引子a/l，而且由于悬臂梁在固定端的应力是最大的，所以可知杆的弯曲应力比起拉压应力要小一个数量级。因此，在分析桁架的受力时，它各杆的弯曲应力是可以略去的。这就是为什么在分析桁架时假定节点是铰接的原因。

有一点需要附加说明的是，对于荷载都作用在节点上的假设，纯粹是为了在分析受力时没有受弯曲的杆件。如果有某一根杆外载是加在杆中间，那也很容易办，先把载荷等效地分配到临近的节点上分析桁架，然后只要对这根杆当作实际载荷与反向的等效载荷作用的梁来分析，把分析结果与桁架得到的结果相叠加就可以了。

以上对桁架所受弯曲的讨论，纯粹是从数量级上来考虑的，因为所设的条件都是不利的情况，实际情况远比所讨论中的弯曲应力要小许多。所以通常分析桁架，都可以放心地只考虑每根杆受拉力或压力就可以了。不过有时候还是需要仔细讨论桁架中杆件所受的弯曲情况的，例如在超静定结构中，有的杆变形比较大，已经超过比例极限产生了塑性变形，或者结构对变形的要求比较精密，需要考虑弯曲所引起的变形，这时候就需要考虑桁架所有杆的弯曲。这种分析的结果称为桁架的二次应力。

人们在研究自然界或人造的事物，都需要进行一定的简化，去抓住事物最主要的本质特点，这就是模型化的方法。桁架就是结构力学中最重要的一类模型。