抛物线的中点生成算法_最小生成树和拓扑排序

这个是给19学弟学妹的，糊了大半天糊不动了，明天再修补修补吧。

我们这次学什么

• [1] 最小生成树
• [2] 拓扑排序
• [3] 一点点我觉得有意思的东西

最小生成树（Minimum Spaning Tree）

在无向图

中，生成树指的是，一个生成子图（该子图包含所有原图中的点，即

）是一棵树。对于一个带权的无向连通图，必然存在一个或多个生成树，使得它的各边权值和是最小的，我们就把它称为最小生成树。关于这个最小生成树有什么用，比如想要铺建一个网络线路网中，要让这个网络上每家每户（可以看作节点）都能通网，我们利用这个最小生成树就可以找到最经济的铺设线路的方法。

Kruskal算法

步骤

1. 按权值对所有的边进行排序。
2. 排序后枚举每一边，如果添加某一条边到生成树中不会产生圈的话（可以使用并查集实现），那么将这条边加入生成树中。一直生成树生成完成结束。

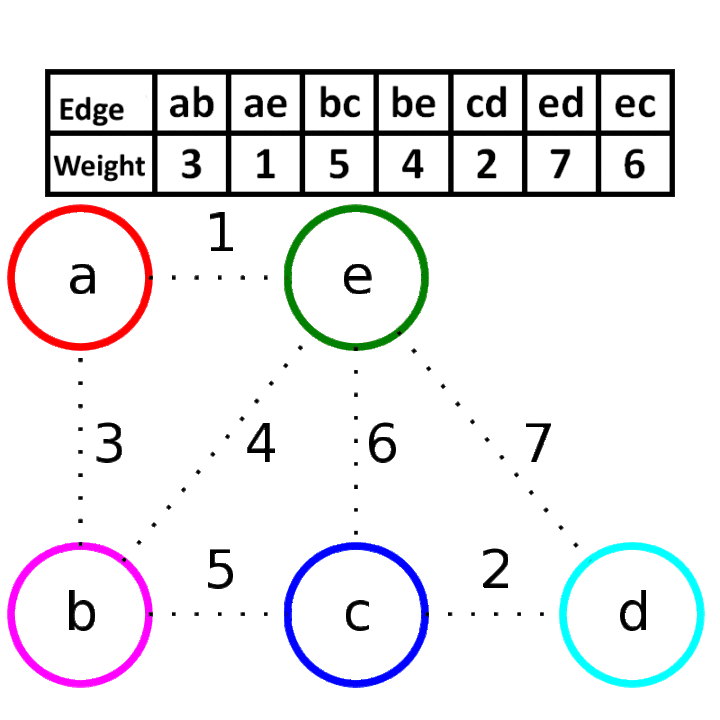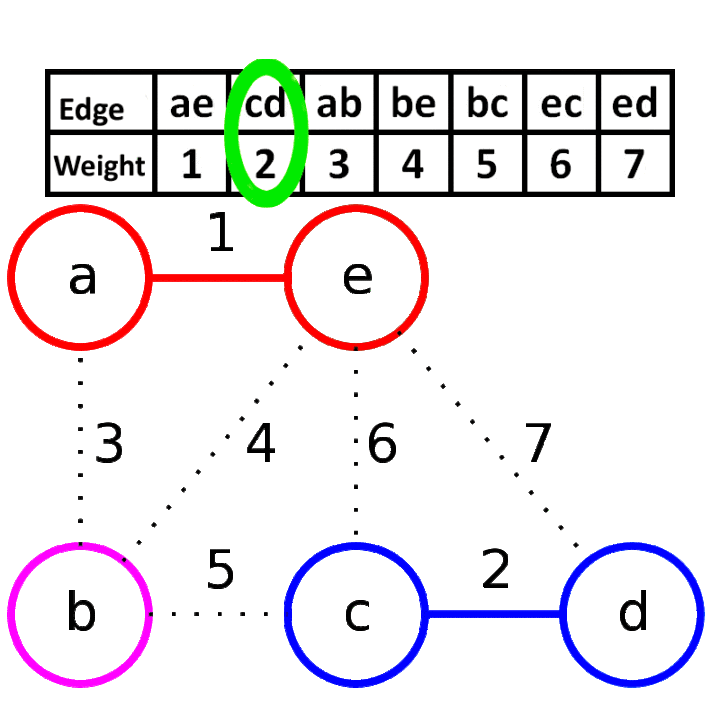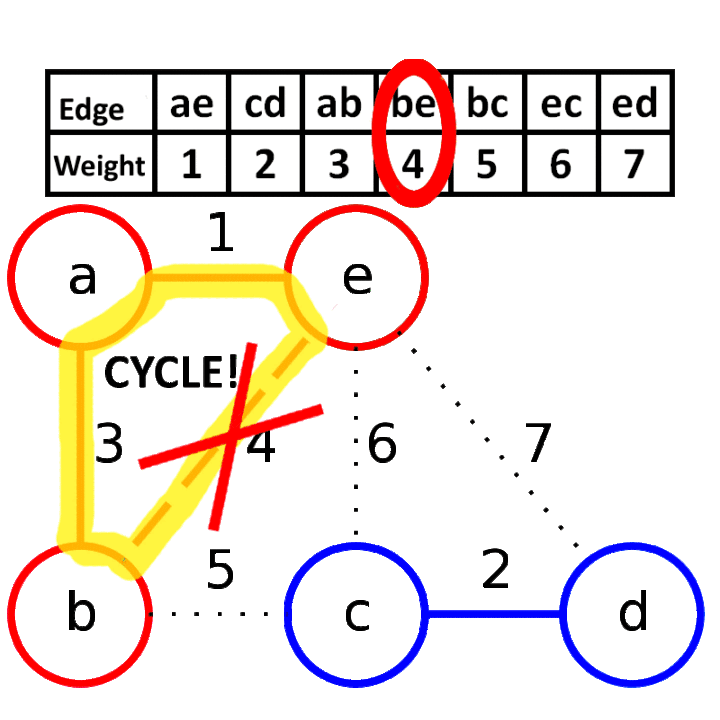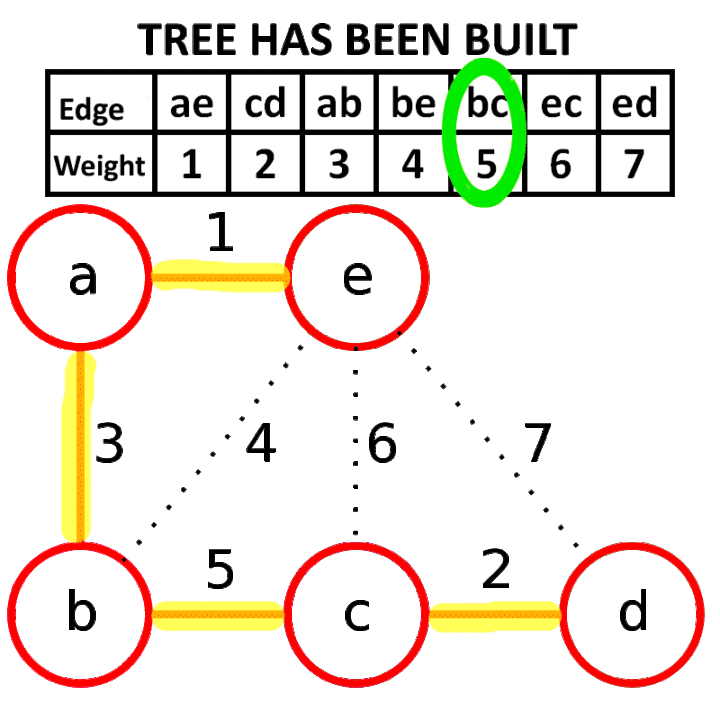
复杂度为

(主要排序的复杂度)。 稀疏图较快。

证明

1. 首先它一定是棵树（因为并查集那步要避圈呐）。
2. 下面证最小。

• 1 令
  是算法得到的树，
  是权最小的生成树。如果
  我们选取
  中第一条和
  不同的边
  。将
  加入
  中，这次
  中必然会形成一个环
  。与此相对应的环
  中肯定也有一条边
  不在
  中。那我们构造一棵树
  。
• 2 假如
  的权大于
  的权，说明边权
  大于
  ，但是要是真的对
  中的
  之前已选部分（这部分添加进
  或
  不成圈）继续选边，按照之前的算法，是要保证
  的，与我们的假设矛盾，所以
  。
• 3 我们重复上述过程（每次找其它不同边），最后可以证明

呆码

ll kruskal(){
    ll i, ednum=0;
    ll res=0;
    sort(ed+1, ed+cnt+1, cmp);
    for(i=1; i<=cnt; i++){
        if(getfa(ed[i].fo)!=getfa(ed[i].to)){
            merge(ed[i].fo, ed[i].to);
            res+=ed[i].w;
            ednum++;
        }
        if(ednum>=vn-1) break;
    }
    return res;
}

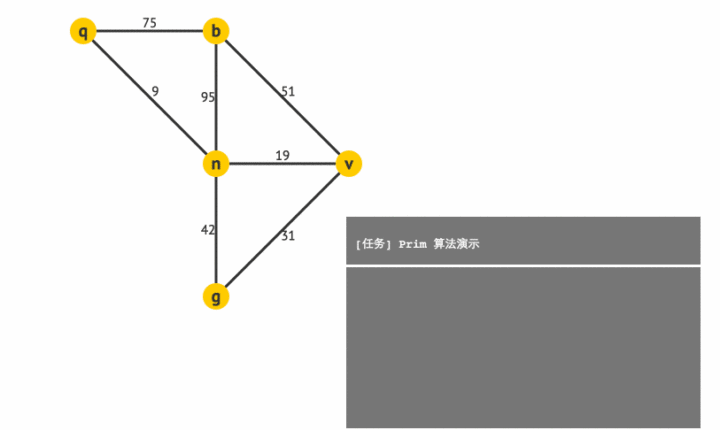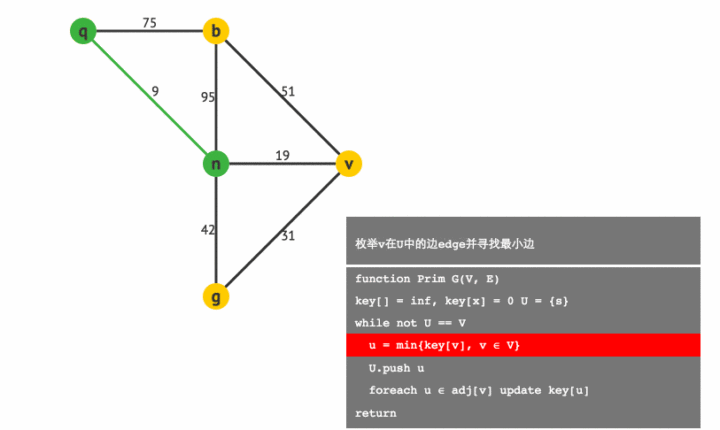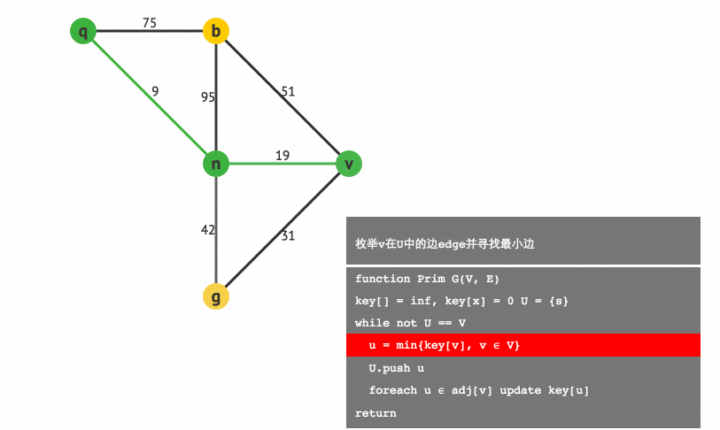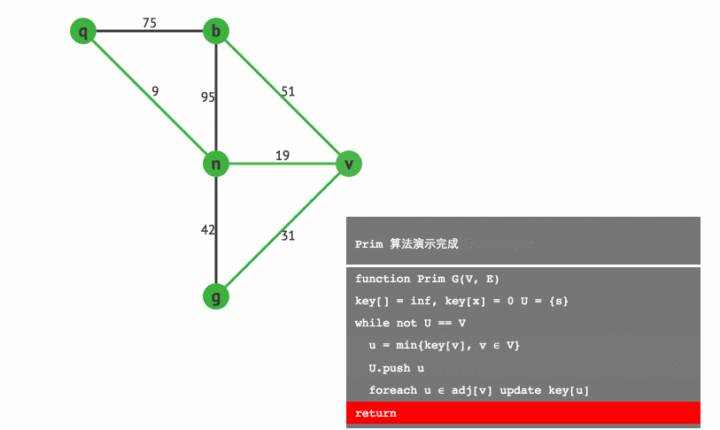
Prim算法

步骤

1. 任取一个点初始点
   加入集合
   。
2. 找两端分别连接了集合
   及集合
   (非
   集合中的点的集合)中点的权值最小的边,并将边连接的非
   集合中点加入集合
   。
3. 不断执行步骤2直到得到一颗生成树。

复杂度

，堆优化后

。稠密图上较合适。

证明

显然是棵树。

下面是关于权值最小的证明。可以使用归纳法。

假设现在已求得的生成树的顶点集合为

，并且显然存在一棵最小生成树

使得

覆盖

部分的边集与通过Prim求得覆盖

的边集相同（如果不同，可以把不同的部分切下来换上相同部分，因为两个边集都已保证最小所以不影响权值和）。假设Prim算法该阶段选取的是边

，若

在T中，那好说，直接下一步归纳。如果

不在

，那么

中肯定含有一条边

连接

和

。根据我们的选取规则（选最小权的连接两部分的边），

。我们每次归纳都重复该操作，可以最后将

全换为Prim算法选取出的边，并且最终权值和小于等于

，那么结论得证。

呆码

void Prim(){
    int s=1;
    priority_queue<pair<int ,int > > pq;
    mem(vis); mem(pre); //初始化为0
    fill(dis+1,dis+n+1,inf); //dis[1]到dis[n]设置为无穷
    edge[0].len=0;
    dis[0]=0;
    pq.push(make_pair(0,s));
    while (!pq.empty())
    {
        int x=pq.top().second;
        pq.pop();
        if (!vis[x])  //不在集合v0中
        {
            vis[x]=1; //加入集合v0
            ans+=edge[pre[x]].len; //加上最后一次中更新x的边权
            for(int i=head[x]; i; i=edge[i].nex){
                int y=edge[i].to;
                if(dis[y]>edge[i].len){ //更新到集合中的距离
                    dis[y]=edge[i].len;
                    pq.push(make_pair(-dis[y],y));  //priorqueue默认建的大顶堆，最大的最先，所以取负
                    pre[y]=i;  //更新
                }
            }
        }
    }
}

拓扑排序（Topological sorting）

拓扑排序解决的问题是给图中节点进行排序。

比如说选课里面的先行课，只有修了C语言后才能修数据结构，修了数据结构后就可以进行编译原理等的通关游戏。假设这个叫迭代学习。

要是你学计组的时候发现电路看不懂，先补一波数字逻辑再来看计组，补数字逻辑的时候又发现不理解晶体管的工作原理于是先补一波大学物理（以上纯属虚构）。我们假设这个叫递归学习。

万一，某天发现人培上写要学java得先学python、python的先行课却又是java（显然这个不可能），我们假设为死循环学习。

拓扑排序就可以对这些课进行排个序，可以判断出是否有死循环学习，然后可以将递归学习变迭代学习。

我们对这个模型建图，假设课程

是课程

的先行课（

对

有依赖关系），那么可以引一条有向边由

指向

。假如它能成功拓扑排序，那它必是一个有向无环图（DAG）（如果有环就会有一对节点相互依赖，就死循环学习了）。相应的有向无环图可以拓扑排序（可以归纳法证明一下）。

Kahn算法

主要想法是维持入度为0的点。

1. 将所有入度为0且未访问过的点加入集合
   。
2. 遍历集合
   中所有点并把这些点从集合中删除，遍历以这些点为起点的边，并且每次遍历边时都将边的终点的入度减1。
3. 重复步骤1，2直到集合
   为空。

如果该图不是一个有向无环图的话，必然会有点重复入队列，那就多开个数组判断一下吧。

复杂度

。

代码

queue<ll > q;
for(i=1; i<=n; i++){
    if(!in[i]){ //入度为0
        q.push(i);
        ord[i]=1;  //记录到达该点的最长路径
    }
}
while (!q.empty())
{
    ll x=q.front();
    q.pop();
    for(j=head[x]; j; j=edge[j].next){
        ll y=edge[j].to;
        ord[y]=max(ord[y],ord[x]+1);
        in[y]--; //入度--
        if(!in[y])
        {
            q.push(y);
        }
    }
}

一些我觉得还蛮好玩的东西

建图

这个网站输入点和边，可以可视化图形出来，有些图论题放进去对比对比样例还是阔以。

邻接矩阵

假如这边的

表示

和

之间的连边数。

比如、

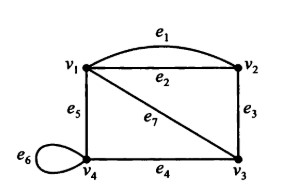
对应的邻接矩阵便为

1. 假设
   是
   的邻接矩阵，则
   中的元素
   表示的是从点
   到
   的长度为
   的路径条数。
2. 敲不动了，上图吧。

END