差分约束最大化最大值减最小值_PDE有限差分方法(2)——范数回顾、符号演算、基本概念...

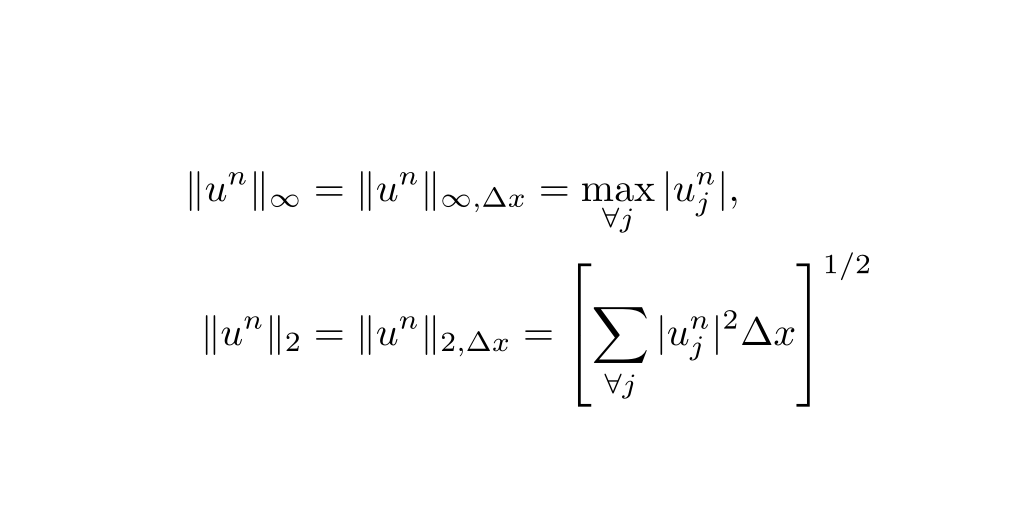
今天的笔记中，主要回顾一下数值计算里面的范数理论（不学偏微分方程数值解但是学数值计算的同学也完全可以用它来复习），再复习一下符号演算（其实这也是数值计算里面涉及的内容）。最后定义空间网格函数的离散范数.

参考书：
(1) J.W. Thomas - Numerical Partial Differential Equations_ Finite Difference Methods (1995, Springer)
(2) 张强《偏微分方程的有限差分方法》科学出版社，2019年1月版。
(3) K. W. Morton, D. F. Mayers - Numerical solution of partial differential equations (2005, Cambridge University Press)

本次主要内容：

1 向量范数、矩阵范数、谱半径回顾

这部分如果学过泛函分析，也可以跳过.

定义1.1 [向量范数] 设

. 若在

上定义了个实值函数,

满足下面三个条件:

(1)非负性:

且

(2)齐次性:

(3)三角不等式:

则称

为

的一种

范数, 并说

是赋以范数

的

赋范线性空间.

常见的三种向量范数：

其中2范数又叫Euclid范数. 用Euclid范数可以诱导内积，从而得到Cauchy-Schwarz不等式.

定理1.2

中的向量范数都是等价的, 即任两种范数

总存在两个与x无关的正常数

使得

注：在泛函分析中，有限维赋范线性空间中的范数都是等价的, 利用n维有限维赋范线性空间同构于

即可证明.

证明：只需证任一种范数

与

等价. 设

是范数

下的一组基, 由Cauchy-Schwarz不等式,

则

所以范数

关于

范数是x的连续函数.

由于

中单位球面

是有界闭集, 则

可在S上达到最大值

与最小值

对任意的

令

则

因为

所以

所以

QED

定义1.3 [矩阵范数] 设

若在

中定义了一个实值函数, 记作

满足如下条件:

则称

为矩阵A的一种

范数.

定义1.4 [相容]若在

中定义了一种矩阵范数

在

中定义了一种向量范数

若对

中的任何一个矩阵A和

中的任何一个向量

恒有不等式

成立, 则说上述矩阵范数和向量范数 相容.

定理1.5 设

是任意矩阵范数, 则在

中至少存在一种向量范数

使得

和

相容.

证明：设

取

就是这样的一种向量范数. 3个条件不难验证, 相容性也不难验证. QED

定义1.6 [从属]假设矩阵范数

和向量范数

相容, 且对每一个

都存在一个非零向量

(与A有关), 使得

则说

是

从属于向量范数

的矩阵范数.

命题1.7 如果矩阵范数

是从属于向量范数

则

证明：作业.

定理1.8 对于

中的每一个向量范数

中至少存在一种从属于它的矩阵范数, 定义

就是这样一种矩阵范数.

证明：只需证相容性. 对于任意非零

构造一个单位向量为

则

所以

(要注意

是个常数). 把相容性证完以后, 就可以证明矩阵范数定义的条件(4):

QED

定理1.9 [矩阵的1,2,

范数] 把前面定理

中的向量范数取特定的

范数, 可以得到具体的矩阵范数, 相应记为

记

则

又称为

谱范数.

注：记忆方法：“1”是竖着写的，所以是列和的max；“

”是横着写的，所以是行和的max。

证明：略.

定理1.10 [Frobenius范数]

即所有元素的平方和再开方, 它是个矩阵范数.

注：由于

它不从属于任何范数.

命题1.11 Frobenius范数与

范数相容. (作业)

命题1.12 设A是n阶实对称矩阵, 特征值为$$,

则

证明：由于A是对称的, 则

所以

QED

定理1.13[相容] 设

是两个矩阵范数, 则存在

使得

定义1.14 [谱半径]设

记

表示A的谱半径. 其中

是A的特征值.

注：

定理1.15 对于

中任何矩阵范数

恒有

证明：由前面某定理, 存在

中向量范数

使得对一切

都有

又设

是任一特征值,

是对应的特征向量, 则

于是

由

的任意性, 则

QED

定理1.16 设

对于任意给定正数

在

中至少存在一种矩阵范数

使得

证明：我认为不是这门课的重点. 略.

命题1.17 对

中任意范数

都有

(作业)

命题1.18 对

中任意范数

若A是非奇异矩阵, 则

（作业）

定理1.19[酉变换的不变性] 设

在酉变换下, 谱范数

和Frobenius范数

保持不变, 即设

则

且

证明：考虑特征值，正交变换（酉变换）不改变特征值的模.

命题1.20 设

则

(作业)

定义1.21[条件数] 对于

定义它所用范数的

条件数为

条件数越大，说明数值方法不好.

其他定义与定理在用到的时候再提出.

最后，再引入一个Gershgorin圆盘定理.

定理1.22 [Gershgorin第一圆盘定理]下列复平面中

个圆盘

的并

包含

矩阵

的谱（即所有特征值构成的集合）. 换言之，对任意特征值

存在

使得

证明：设

是

的谱中任意元, 选择一个向量

, 使得

且

设

是

的一个指标. 因为

所以

则

因此

QED

2 符号演算技巧

设h是给定的移位距离, 移位算子

则

反向移位算子

是

的逆.

各种差分离散算子都可以用移位算子表示, 例如

• 一阶向前差分算子:
• 一阶向后差分算子:
• 一步中心差分算子:
• 半步中心差分算子:
• 二阶中心差分算子:

符号演算技巧：把算子符号记作变量, 算子运算变成函数运算.

注：差分算子的各个系数加起来是0, 平均算子

不能用差分算子表示.

例2.1 建立微分算子

的差商导数, 用向前差分来表示.

解：由Taylor展开, 可知

可以用差商表示为:

由

可知

由

的Taylor展开, 且

则

注：如果把上述算子作用于

得到的

系数加起来为0.

如果改用

的有理逼近技术

可得

其中除法对应左逆操作.

利用函数

的Taylor展开式(有理逼近公式), 可以证明下面的函数逼近公式: （作业）

3 离散范数、差分方程的格式描述方式

定义3.1 [网格函数]空间网格

与时间网格

的笛卡尔乘积构成

时空网格

这里都是等距网格, 为了简单期间我们默认

是等距的, 其中

是

时间步长,

是空间步长. 定义在离散网格

或其子集上的离散函数(指

定义域是个离散点集的函数) 通常称为 网格函数.

叫

网格点.

发展型方程通常用逐层推进求解的策略. (即按照时间来推进) 因此任意时刻(尤其是终止时刻)的空间网格函数

是备受关注的研究对象.

空间网格函数的度量有两种. ①逐点度量(简单直观的逐点方式); ②离散范数(适合整体方式). 通常用下面的离散范数: (接近于向量范数)

这2个范数都满足范数的定义, 类比

空间即可. 与一般范数的区别在于它与

网格空间步长有关.

例如在

区间上,

则

(复合型矩形积分公式) 其中

是

在区间

经过各个点的插值函数.

差分方程有两种描述方式：

(1)简单直观的局部描述, 即位于网格点的差分方程, 例如

是热传导方程在

点处的一个离散逼近. 展开来写就是

(2)理论严谨的整体描述, 即逼近模型问题的完整离散系统

其中

是时间步长,

是

时刻的

网格函数,

是给定的网格函数(初边值),

和

是网格函数空间到其自身的线性算子. (其实它们可以与时间层数和网格函数有关. 但是若与网格函数有关, 则相应的差分格式是非线性的.)

默认

是可逆的(要满足格式运行的可行性), 定义相应的

规范形式

其中

若两个差分格式的规范形式相同, 那么它们是

没有差别的.

注：规范形式是唯一的.

加密路径

严格来讲, 差分格式不是特指某个固定网格的一个离散系统, 是指同网格参数相关的一族离散系统. 在网格的加密过程中, 差分格式的数值现象是重要的研究内容. 这两个网格参数可以独自趋于零(用的少), 但是通常假定它们沿着某种加密路径

趋于零, 其中

是满足

的连续函数.

下图中的加密路径, 实线表示

是常数, 虚线表示

是常数.

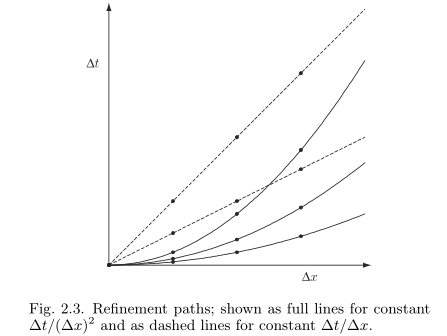
若某个数值概念（即将介绍的相容性、稳定性和收敛性）对于任意的加密路径都是成立的, 则称这个数值概念是无条件成立的；否则称其是有条件成立的.