堆一定是完全二叉树_（十一）排序----堆

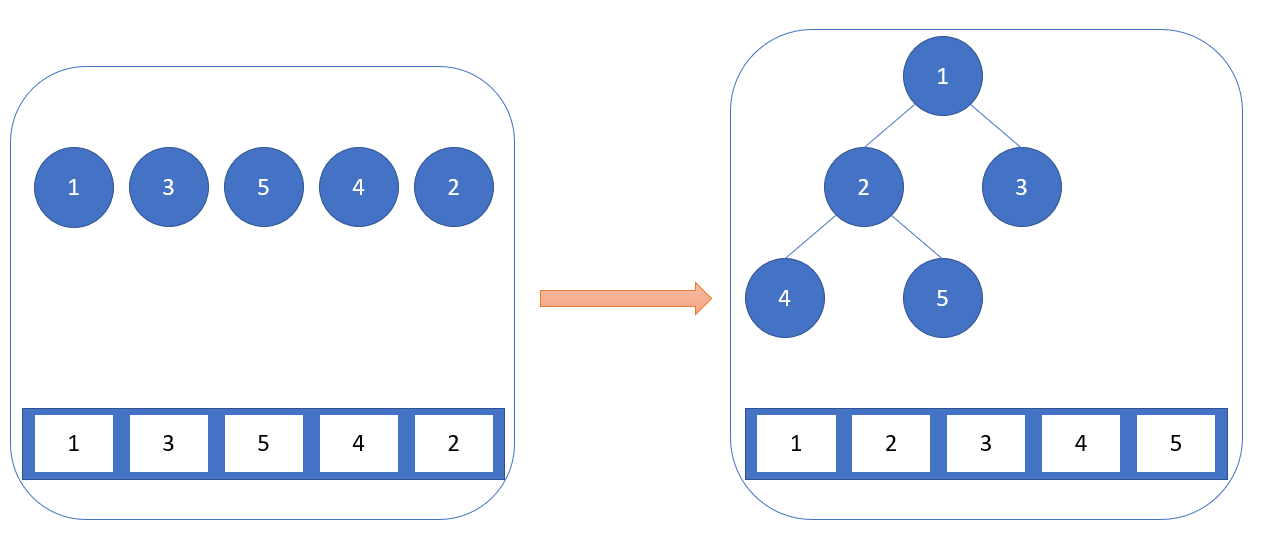
源于生活，抽象生活。

欠下的债总是要还的，我们讨论堆排序，用到的就是二叉堆，聊起二叉堆，我们又要反过来倒回到之间介绍的二叉树系列。

生活中的堆排序

一提二叉树，我总是想起来挂在老家的家谱，可惜不能拍照。

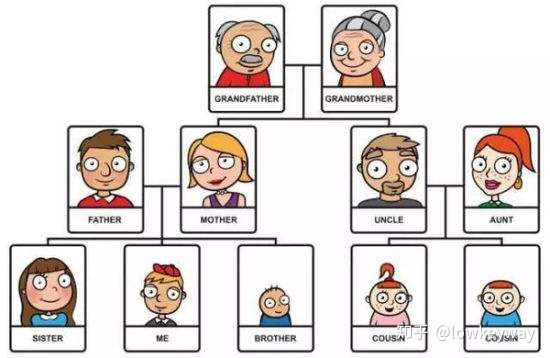
这就是严格的等级排序，最上面的就是辈分最大的，最下面的，就是辈分最小的。

计算机中的堆排序

貌似我们有好多东西要讲。千里之行，始于足下。一个个来吧。

什么是堆排序？

就是利用二叉堆的特性进行排序的方式。

那什么又是二叉堆？它有什么特性？

二叉堆本质上就是一种完全二叉树，它分为两种：

• 最大堆：任何一个父节点的值，都大于或等于它左、右孩子节点的值。
• 最小堆：任何一个父节点的值，都小于或等于它左、右孩子节点的值。

可以想象：最大堆的堆顶是整个堆的最大元素，最小堆的堆顶是整个堆的最小元素。

什么是完全二叉树？

那我建议还是先返回去看看二叉树的实现那一节。

只有最后两层的节点的度能小于2，并且最后1层的叶子节点必须靠左边。这样的树就叫完全二叉树。

它有个特点：将整个完全二叉树依照从左到右，从上到下的进行0-->n进行编号，若子节点序号为i,则父节点为(i-1)/2。

文字好无力，还是公式和图好：

这就是完全二叉树

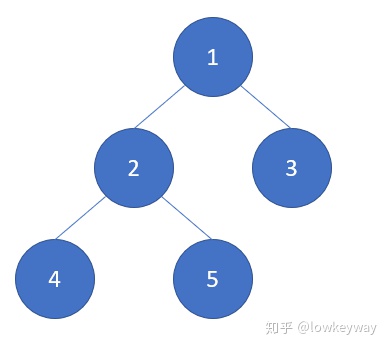
我们先用代码来实现以下完全二叉树。

老规矩，还是要先写大纲，再下笔：

1. 我们要写一个二叉堆，它是一个完全二叉树。
2. 跟之前写的二叉树有些不同的是，这个二叉树不是链表构成的，而是数组下标查询的。因为是完全二叉树，那么如果父节点的下标是parent，左孩子的小标就是2parent+1，右孩子下标就是2*parent+2.
3. 它应该带有自我构建的功能，就是说对于一个无需的数组，它应该可以自己把最大/最小值上浮，最后达到最大堆/最小堆的特征需求。

注意点：

1. 在下沉元素时，必须要从下到上一次轮询；
2. 轮询过程中，一定要下沉到不能下沉为止。

BinTree.h

#ifndef __BIN_TREE_H__
#define __BIN_TREE_H__

#include <string>
#include <iostream>

#ifndef SWAP(X, Y)
#define SWAP(X, Y) (X)=(X)+(Y);(Y)=(X)-(Y);(X)=(X)-(Y)
#endif // !SWAP(X, Y)



using namespace std;

typedef enum BigLittle
{
	BIG = 0,
	LITTLE = 1
}BIG_LITTLE;

class BinTree
{
public:
	BinTree(int* p, int cap);
	~BinTree();
	bool buildHeap(BIG_LITTLE bl);
	bool showBinTree();

public:
	int* m_piBinTree;
	int  m_iCap;
	int  m_iCount;
};


#endif // !__BIN_TREE_H__

BinTree.cpp

#include "binTree.h"


BinTree::BinTree(int* p, int cap)
{
	if (cap <= 0)
	{
		cout << "Please input correct number!" << endl;
		return;
	}

	m_piBinTree = new int[cap];
	if (NULL == m_piBinTree)
	{
		cout << "BinTree NEW fail!" << endl;
		return;
	}

	memset(m_piBinTree, 0, sizeof(int)*cap);
	memcpy(m_piBinTree, p, sizeof(int)*cap);

	m_iCap = cap;
	m_iCount = 0;
}

BinTree::~BinTree()
{
	delete[]m_piBinTree;
}

bool BinTree::showBinTree()
{
	if (m_iCap <= 0)
	{
		cout << "Please init BinTree frist!" << endl;
		return false;
	}

	cout << "BinTree: " << endl;
	for (int i = 0; i < m_iCap; i++)
	{
		cout << m_piBinTree[i] << " ";
	}
	cout << endl;

	return true;
}

bool BinTree::buildHeap(BIG_LITTLE bl)
{
	int childIndex, parentIndex;
	if (m_iCap <= 0)
	{
		cout << "Please init BinTree frist!" << endl;
		return false;
	}
	m_iCount = 0;
	for (int i = (m_iCap - 2) / 2; i >= 0; i--)
	{
		if (BIG == bl)
		{
			parentIndex = i;
			childIndex = 2 * parentIndex + 1;
			while (childIndex < m_iCap)
			{
				if (childIndex + 1 < m_iCap && m_piBinTree[childIndex] < m_piBinTree[childIndex + 1])
				{
					childIndex++;
				}

				if (m_piBinTree[parentIndex] < m_piBinTree[childIndex])
				{
					SWAP(m_piBinTree[parentIndex], m_piBinTree[childIndex]);
				}

				parentIndex = childIndex;
				childIndex = 2 * childIndex + 1;
				m_iCount++;
			}
		}
		else if (LITTLE == bl)
		{
			parentIndex = i;
			childIndex = 2 * parentIndex + 1;
			while (childIndex < m_iCap)
			{
				if (childIndex + 1 < m_iCap && m_piBinTree[childIndex] > m_piBinTree[childIndex + 1])
				{
					childIndex++;
				}

				if (m_piBinTree[parentIndex] > m_piBinTree[childIndex])
				{
					SWAP(m_piBinTree[parentIndex], m_piBinTree[childIndex]);
				}

				parentIndex = childIndex;
				childIndex = 2 * childIndex + 1;
				m_iCount++;
			}
		}
		else
		{
			cout << "SomeThing Wrong!" << endl;
			return false;
		}
	}

	return true;
}

测试程序

#include "MySort.h"
#include "binTree.h"

#define LEN(X) (sizeof(X)/sizeof(X[0]))

using namespace std;


int myArray[] = { 1, 3, 5, 7, 9, 10, 8, 6, 4, 2 };

int main()
{
	//MySort M(myArray, LEN(myArray));
	//M.bubbleSort(DOWN);
	//M.fasteSort(DOWN);

	BinTree B(myArray, LEN(myArray));
	B.showBinTree();
	B.buildHeap(BIG);
	B.showBinTree();
	B.buildHeap(LITTLE);
	B.showBinTree();
	system("pause");
	return true;
}

输出结果

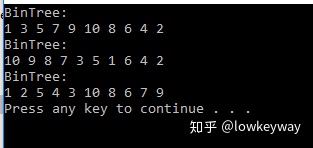
好了，我们实现了二叉堆，那么我们怎么利用二叉堆来实现二叉堆排序呢？

很简单，以最大堆为例：

1. 我们知道，cap(cap要大于等于1)大小的数组二叉堆排序后堆顶肯定是这个堆的最大值；
2. 我们可以把堆顶的元素跟堆尾的元素交换；
3. 以cap-1这么大的数组再做一次二叉堆排序，循环到1；
4. 直到cap减小到0，那么这个时候数组存储的二叉堆就变成了一个升序排列；

有了方法，用代码来实现：

注意事项：

1. 貌似没什么可注意的，思路清晰了，代码简洁没什么难度。

MySort.h

#ifndef __MY_SORT_H__
#define __MY_SORT_H__

#include <iostream>
#include <string>
#include "binTree.h"


typedef enum UpDown
{
	UP = 0,
	DOWN = 1
}UP_DOWN;

class MySort
{
public:
	MySort(int* p, int cap);
	~MySort();

	bool showArray(int* p, int len);

	bool bubbleSort(UP_DOWN Up_Down);
	bool fasteSort(UP_DOWN Up_Down);
	bool fastSortImp(int *pFast, int iCap);
	bool binTreeSort(UP_DOWN Up_Down);

public:
	int* m_ipArray;
	int m_iCap = 0;
	unsigned long m_ulCount;
};

#endif // !__MY_SORT_H__

MySort.cpp

增加binTreeSort接口

bool MySort::binTreeSort(UP_DOWN Up_Down)
{
	DWORD count = 0;
	BIG_LITTLE bigLittle = Up_Down == UP ? BIG : LITTLE;

	if (m_iCap <= 0)
	{
		cout << "Please input array frist!" << endl;
		return false;
	}

	int* pBinTree = new int[m_iCap];
	if (NULL == pBinTree)
	{
		cout << "New Fail!" << endl;
		return false;
	}

	m_ulCount = 0;
	memset(pBinTree, 0, sizeof(pBinTree[0]) * m_iCap);
	memcpy(pBinTree, m_ipArray, sizeof(pBinTree[0]) * m_iCap);

	BinTree B(pBinTree, m_iCap);
	for (int i = m_iCap - 1; i > 1; i--)
	{
		B.buildHeap(bigLittle);
		SWAP(B.m_piBinTree[0], B.m_piBinTree[i]);
		B.m_iCap--;
		m_ulCount += B.m_iCount;
	}

	memcpy(pBinTree, B.m_piBinTree, sizeof(pBinTree[0]) * m_iCap);

	showArray(pBinTree, m_iCap);
	printf("BinTree Sort takes [%lu] Times when n = [%d] n", m_ulCount, m_iCap);


	delete[]pBinTree;
	return true;
}

测试程序：

#include "MySort.h"
#include "binTree.h"

#define LEN(X) (sizeof(X)/sizeof(X[0]))

using namespace std;


int myArray[] = { 1, 3, 5, 7, 9, 10, 8, 6, 4, 2 };

int main()
{
	MySort M(myArray, LEN(myArray));
	M.bubbleSort(DOWN);
	M.fasteSort(DOWN);
	M.binTreeSort(DOWN);

	//BinTree B(myArray, LEN(myArray));
	//B.showBinTree();
	//B.buildHeap(BIG);
	//B.showBinTree();
	//B.buildHeap(LITTLE);
	//B.showBinTree();
	system("pause");
	return true;
}

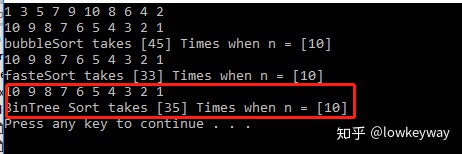
运行结果：