java kdtree_KdTree说明

概述

Kd-Tree，即K-dimensional tree，是一种高维索引树形数据结构，本身是一二叉树， 树中存储的是一些K维数据。在一个K维数据集合上构建一棵Kd-Tree代表了对该K维数据集合构成的K维空间的一个划分，即树中的每个结点就对应了一个K维的超矩形区域 。常用于在大规模的高维数据空间进行最近邻查找(Nearest Neighbor)和近似最近邻查找(Approximate Nearest Neighbor)，例如图像检索和识别中的高维图像特征向量的K近邻查找与匹配。

2D对应的KD平面划分

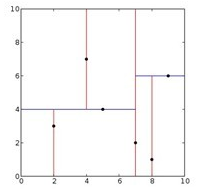
KdTree主要分三大部分

KdTree的构建

最近邻域查找算法

KdTree增删节点

节点

节点类型

变量名

类型

描述

m_SplitNodeDataIndex

int

节点存储的数据在源数据的位置索引

m_SplitDimentionIndex

int

垂直于分割超平面的方向轴索引

m_isDeleted

bool

节点是否删除的标志

m_LeftChild

CKdNode*

位于该节点分割超平面左子空间内所有数据点构成的Kd树

m_RightChild

CKdNode*

位于该节点分割超平面右子空间内所有数据点构成的Kd树

m_Parent

CKdNode*

父节点

int m_SplitDimentionIndex;

int m_SplitNodeDataIndex = -1;

bool m_isDeleted = false;

CKdNode* m_Parent = nullptr;

CKdNode* m_LeftChild = nullptr;

CKdNode* m_RightChild = nullptr;

KdTree的构建(递归思想)

构建KdTree算法流程如下： 1 .若CSouceDataSet为空，则返回空Kd Tree；

2 .节点生成：

( 1 )确定m_SplitDimentionIndex： 统计所有数据CSouceDataSet在每一维上的数据方差，然后比较各个维度的方差，挑选出最大值，对应的维度就是m_SplitDimentionIndex，方差大表明该坐标轴方向上数据分散的开，进行分割有较好的分辨率

( 2 )确定m_SplitNodeDataIndex： 对数据CSouceDataSet按其第m_SplitDimentionIndex维的值排序，位于中间的那个数据点对应的索引作为m_SplitDimentionIndex，若CSouceDataSet的个数为偶数，中间值为number/2前后两个点均可。此时新的newCSouceDataSet =CSouceDataSet\Node-data(除去其中m_SplitNodeDataIndex对应的数据点)。

3 .左子空间和右子空间

分割超面k=CSouceDataSet[m_SplitNodeDataIndex][m_SplitDimentionIndex]将整个空间分为两部分。CSouceDataSet[i][m_SplitDimentionIndex]<=k 为左子空间，另一部分为右子空间。

数学表示方法：

dataleft = {d属于newCSouceDataSet && d[i][m_SplitDimentionIndex] ≤ CSouceDataSet[m_SplitNodeDataIndex][m_SplitDimentionIndex]}

Left_Range = {Range && dataleft}

dataright = {d属于newCSouceDataSet && d[i][m_SplitDimentionIndex] > CSouceDataSet[m_SplitNodeDataIndex][m_SplitDimentionIndex]}

Right_Range = {Range && dataright}

4 .左子树和右子树构建

LeftChild = 由(dataleft，Left_Range)建立的KdTree，即递归调用 __buildKdTree(dataleft，Left_Range)。并设置LeftChild 的parent域为vRoot； RightChild = 由(dataright，Right_Range)建立的k-d tree，即调用 __buildKdTree(dataleft，Left_Range)。并设置RightChild 的parent域为vRoot。

核心对应的代码：

for (int i = 0; i < InstanceNum; ++i)

{

if (SplitAttributeValues[i] == SplitValue && vRoot->isEmpty())

{

vRoot->setSplitNodeDataIndex(vDataIndexSet[i]);

vRoot->setSplitDimention(SplitDimentionIndex);

}

else

{

if (SplitAttributeValues[i] <= SplitValue)

LeftChildDataIndexSet.push_back(vDataIndexSet[i]);

else

RightChildDataIndexSet.push_back(vDataIndexSet[i]);

}

}

if (LeftChildDataIndexSet.size() > 0)

{

vRoot->setLeftChild(new CKdNode());

vRoot->getLeftChild()->setParent(vRoot);

__buildKdTree(vRoot->getLeftChild(), LeftChildDataIndexSet);

}

if (RightChildDataIndexSet.size() > 0)

{

vRoot->setRightChild(new CKdNode());

vRoot->getRightChild()->setParent(vRoot);

__buildKdTree(vRoot->getRightChild(), RightChildDataIndexSet);

}

最近邻域查找算法

距离度量方式：MP相异度 算法流程：

1. 从根节点开始，递归向下遍历，一旦找到叶子节点，就将该节点保存为“当前最佳节点”。

2. 回溯，对每个节点执行：

2.1如果当前节点比“当前最佳节点”更接近待查节点，更新该节点为“当前最佳节点”。

2.2检查在分割面的另一边是否有比“当前最佳”离待查点更近的节点。以待查点为中心、以当前最近距离为半径画一个超球面，看这个超球面是否穿过了分割平面。因为平面都是坐标轴对应的，所以只需要简单比较待查点和当前点的在分裂面上的那个维度的差值是否比当前最佳距离小。

2.2.1如果超球面穿越分割面，那么分割面的另外一侧可能有最近点，所以需要递归遍历树的另外的分支，从而寻找更近的点。

2.2.2 如果超球面没有穿过分割面，继续遍历其他节点，但是分割面另外一边的整个分支会被剪掉。

3.当算法最后回溯到根节点的时候，检索完成。

如图所示：(仅供参考)

对应核心代码： 遍历到对应的叶子节点程序： __searchNodeAndPushStack (CurrentNode, vFeatures, NodeStack)

if (vNode == nullptr) return;

while (vNode)

{

vioNodeStack.push(vNode);

int CurrentDataIndex = vNode->getSplitNodeDataIndex();

int CurrentDimentionIdx = vNode->getSplitDimentionIndex();

float GoalFeature = vFeatures[CurrentDimentionIdx];

float CurrentDataFeature = CSourceDataSet::getInstance()->getOneDemensionFeatureValueAt(CurrentDataIndex, CurrentDimentionIdx);

if (GoalFeature <= CurrentDataFeature)

vNode = vNode->getLeftChild();

else

vNode = vNode->getRightChild();

}

超球面穿越分割面情况的代码：

if (voKNerestNeighborIndexSet.size() < vNeighborNum || DistrictDistance < voKNerestNeighborIndexSet.top().m_Distance)

{

float GoalFeature = vFeatures[SplitDimentionIndex];

float CurrentDataFeature = CSourceDataSet::getInstance()->getOneDemensionFeatureValueAt(CurrentSplitDataIndex, SplitDimentionIndex);

//若该节点为父节点的左孩子，父节点存在右孩子，则右子树可能存在更近的点，则遍历右孩子节点；否则，反之

if (GoalFeature <= CurrentDataFeature && CurrentNode->getRightChild())

__searchNodeAndPushStack(CurrentNode->getRightChild(), vFeatures, NodeStack);

else if (GoalFeature > CurrentDataFeature && CurrentNode->getLeftChild())

__searchNodeAndPushStack(CurrentNode->getLeftChild(), vFeatures, NodeStack);

}

增加节点：__addNode2KdTree(unsigned int vGoalIndex)

CKdNode* CurrentSplitNode = new CKdNode();

CurrentSplitNode->setSplitNodeDataIndex(vGoalIndex);

CurrentSplitNode->setSplitDimention(0);

CurrentSplitNode->setParent(ParentNode);

if (IsInLeft)

ParentNode->setLeftChild(CurrentSplitNode);

else

ParentNode->setRightChild(CurrentSplitNode);

删除节点：__deleteNodeFromKdTree(unsigned int vGoalIndex)

找到对应的点将标志设置为已删除状态(并未真正的删除)

while (!PathNodeStack.empty())

{

CKdNode* CurrentNode = PathNodeStack.top();

if (CurrentNode->getSplitNodeDataIndex() == vGoalIndex)

{

CurrentNode->setDeletedSign();

return;

}

PathNodeStack.pop();

if (CurrentNode->getRightChild())

PathNodeStack.push(CurrentNode->getRightChild());

if (CurrentNode->getLeftChild())

PathNodeStack.push(CurrentNode->getLeftChild());

}

代码还可以优化的地方：

寻找CSourceData每维度中间值时，每次都进行排序，消耗时间，可以一次性排序，然后存储起来

在分割超平面上数据点数量不止一个，可以多个，m_SplitNodeDataIndex应设置成数组或vector ...