傅里叶描述子欧氏距离_GPU FFT-基于GPU的快速离散傅里叶变换

从本科到研究生, 稀稀拉拉上了几节傅里叶相关的课, 但一直还是云里雾里. 最近做的工作里面需要平滑笔触的采样点序列, 所以做了一些GPU-FFT的调查, (虽然最后发现不太可能使用在自己的应用场景). 这里记下来, 主要旨在避免以后又得重新来过一次, 这玩意要从头开始搞懂还是比较折磨人的.

快速-离散-傅里叶变换. 每个字段理要解透都是件很痛苦的事情.

首先来理解"傅里叶变换"这个概念. 一个比较好的切入口是从滤波的角度来看.

假设有一个一维函数

, 长的这个样子:

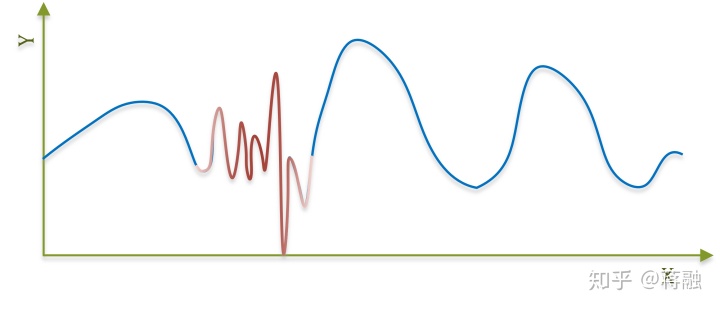
中间那段红色的区域是噪声(高频), 我希望能在尽量保持低频信号形状的前提下, 去掉高频的噪声. 普通的平滑卷积会有收缩(shrink)的副作用, 比较拉跨. 而离散傅里叶可以将函数由值域

变到频域

, 把高频信号干掉, 再回到值域

.

另外一个比较好的例子是多项式乘法, 这个MIT的算法设计课有讲, 感兴趣的可以自行搜, 但是预先警告, 那节课的内容比较硬核, 涉及到递归算法复杂度和非常复杂的算法逻辑.

"离散", 在这个语义之下, (本文只讨论一维)函数/信号在值域和频域都是离散的. 那么应该用什么离散的形式来表示呢?

在值域,

函数

是由

离散的一串采样点组成的. 很多(绝大多)数情况下, 我们拿不到整个函数的解析式, 亦或者解析式非常难以获取. 得到的只是一串采样, 比如雷达按照时序, 每隔一段时间采样一次雷达信号, 或者对于一张图像, 也可以看作是一维/二维的像素序列, 每个像素看作是按相同空间距离均匀的采样点.

值域-采样点序列

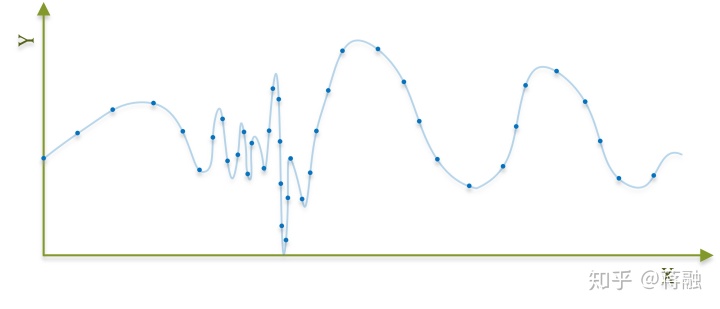
在离散傅里叶变换中, 我们按照采样数

进行均匀采样, 得到以下一组样本序列:

在频域,

函数

是由

离散的一组正&余弦波序列组成的, 波形由三个属性唯一确定:

在值域, 采样时自变量

对应的值就是标量值

; 但是在频域,

一个波形需要3个值才能确定: 频率

,

振幅

, 和

相位偏移

. 那么问题就来了, 应该怎么表示呢? - 复数.

使用复数

可以用来表示振幅

, 和相位偏移

. 复数这玩意, 说白了就是一个有特殊属性的一个二维坐标, 根据欧拉公式:

, 如图:

复数: 复平面上的点

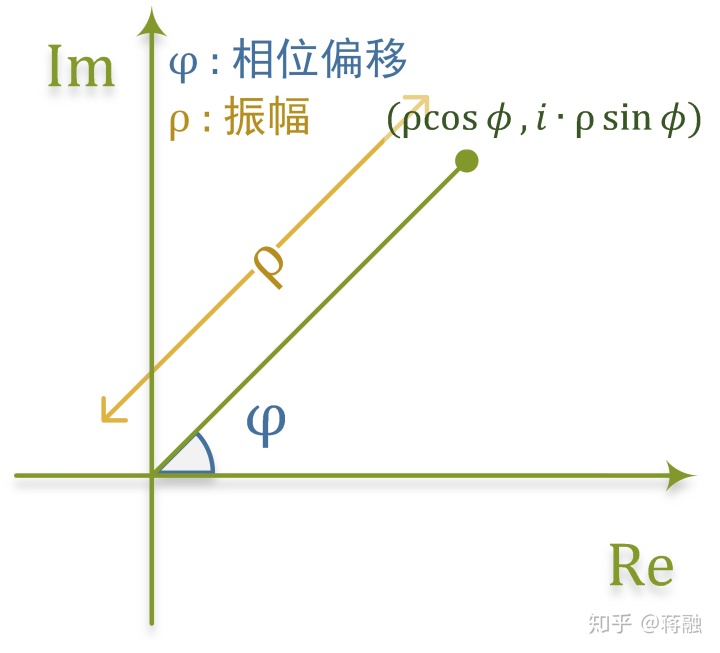
振幅和相位有了, 但是频率

该怎么表示呢? 答案是对复数

再做一点扩展:

这里

表示值域的自变量, 根据实际应用, 可能是时间, 空间坐标, etc. 为了更直观地解释这么做的效果, 可以把这个式子看作一个关于

的函数, 那么随着

均匀增大, 上图的复数点就会开始绕着半径为

的圆

旋转; 并且旋转的频率等于

, 换句话说,

每增大

, 复数点刚好绕圈一周. 如图:

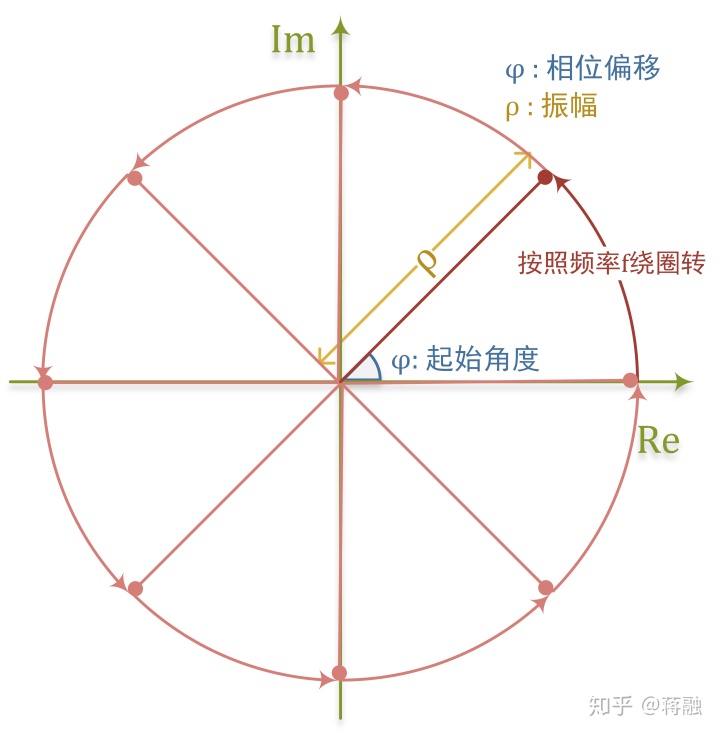
到这里, 三角波的复数形式就已经完备了. 值得注意的是, 这个形式其实复合了一个余弦波和正弦波(复数点按照上图规律旋转时, 实轴和虚轴坐标值的变化分别对应余弦/正弦波).

接下来将

离散化. 这个好办, 将

的值在

区间进行均匀划分:

离散化完成之后的形式: 值域的自变量

每次增1, 复平面上的点都固定转

的角度. 换一个角度也可以看成是上图的圆被均匀分了成

份扇形.

"离散"+"傅里叶变换" == 离散傅里叶

要求得频率

对应的波形

, 我们使用

这组波形作为"basis wave functions",

的求法: 以值域采样值

为混合系数, 把这组基做一个线性组合: (为了方便起见, 这里把

封装成

)

这个公式理解有2条道,

代数解析的观点.

【公开课】斯坦福大学公开课：傅里叶变换及其应用（中英双语）_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili​www.bilibili.com

几何的观点.

3Blue1Brown - 形象的介绍：什么是傅里叶变换？​www.youtube.com

现在只剩一个关键词了-"快速". 那就来谈谈怎么"快速"地做离散傅里叶变换.

最基本的一个并行加速算法叫Cooley-Tuckey, 然后在这个基础上对索引策略做一点改动, 就可以得到适用于GPU的Stockham版本, 据称目前大多数GPU-FFT实现用的都是Stockham.

Cooley-Tuckey算法的核心在于分治思想, 以及离散傅里叶的"Collapsing"特性.

分治思想

通过分而治之的思想, 整个求解过程可以分解成一个树状结构, 更细来讲, 这里我们每次递归都把和式

按照下标n的奇偶性进行二分, 那么求解过程就可以看成一个二叉树:

但是这样还是不够的, 总的复杂度还是

. 每次分治, 子问题的工作量都应该是母问题的一部分(比如一半); 这里我们利用Collapsing的性质, 复杂度就可以减少到

:

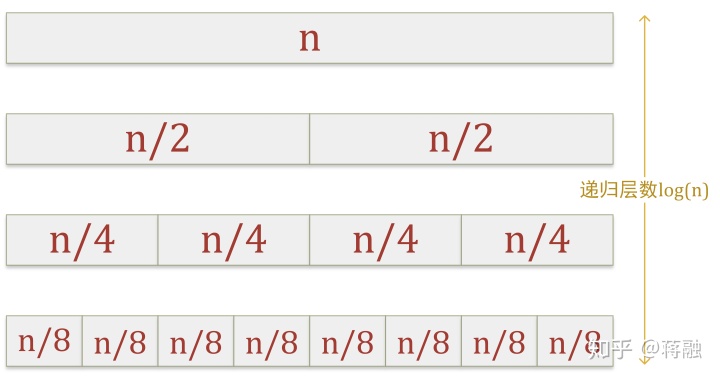
Collapsing性质与蝴蝶变换

接下来谈谈这个collapsing性质, 这个东西是理解FFT的核心, 难, 但是必须弄透澈, 否则没法写代码实现. 先把离散傅里叶的式子再列一下:

为了便于接下来的推导, 更换一下

的表示形式:

新的表达式

包含了分治过程中比较重要的几个部分: 频率

, 样本数

, 以及所有系数(值域采样)

组成的集合

.对于集合

, 把它的元素按照样本序号

的奇偶性分成两等份: (这里我们只考虑总采样数

为2的整数次幂)

那么可以证得如下递归式: (看起来很复杂, 其实构成的部件就只有那几个)

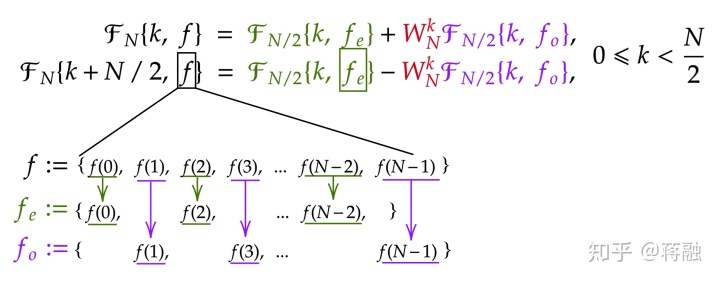
由上图可见, 如果采样量为

,值域样本集合为

,

对于两个频率

做FFT的工作, 可以"坍缩"(collapse)为工作量更小的两个部分:

• 采样量为
  , 样本集合 = 所有原样本集合
  的
  偶数号样本, 对频率
  做FFT
• 采样量为
  , 样本集合 = 所有原样本集合
  的
  奇数号样本, 对频率
  做FFT

上面的式子是从分解(递归)的角度来看的, 但是实际在GPU我们是从树底层开始逐步回溯合并的, 所以这里不妨换到合并的角度. 假设已经算好了两个分部波形:

使用上面的公式, 我们可以合并得到2个更高样本数的频率波形(大名鼎鼎的蝴蝶变换):

蝴蝶变换

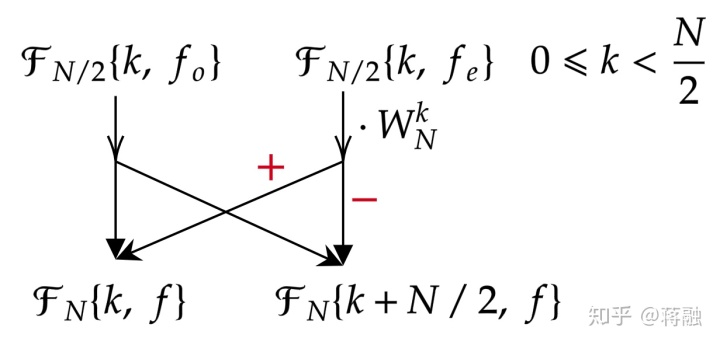
这样, 就实现了工作总量的减半. 接下来谈谈如何利用蝴蝶变换来设计Cooley-Tuckey算法:

如图, 颜色高亮的是每次迭代中的一个蝴蝶变换示例, f是样本集合, k为频率

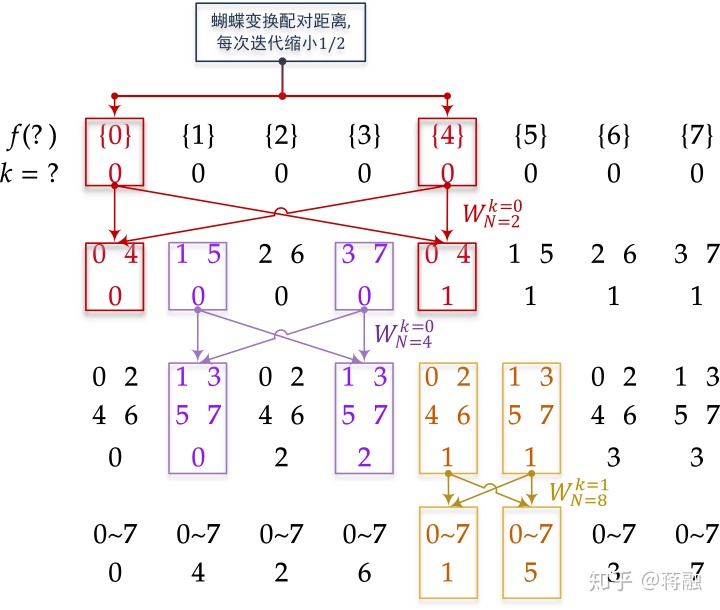
如上图所示, 总的样本数为8, 第一次迭代, 每个波形只有1个样本, 因此对应的频率也只能是0; 经过两两配对的蝴蝶变换, 第二次迭代每个波形包含了2个样本的信息, 频率也扩展到了0, 1, 每次迭代, 蝴蝶变换配对的距离(下标差)减半, 频率数目翻倍...以此类推.

值得注意的是, 这个过程中下标寻址的过程是比较麻烦的. 我们可以在通过调整输出数据的位置, 使每次迭代时, 蝴蝶变换输入的下标遵循一致的pattern. 这就是Stockham的基本思想.

Stockham算法, 注意绿色相框处, 输出波形的排列顺序(自排序)

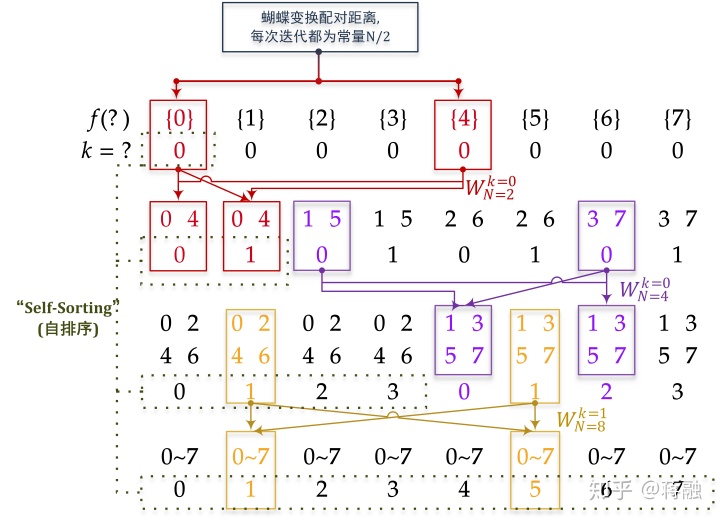
通过上图可以得知, Stockham算法中第

个蝴蝶变换(每轮共有

个蝴蝶变换)对应的 线程

, 它的输入数据(波形)的下标是固定的Pattern:

;

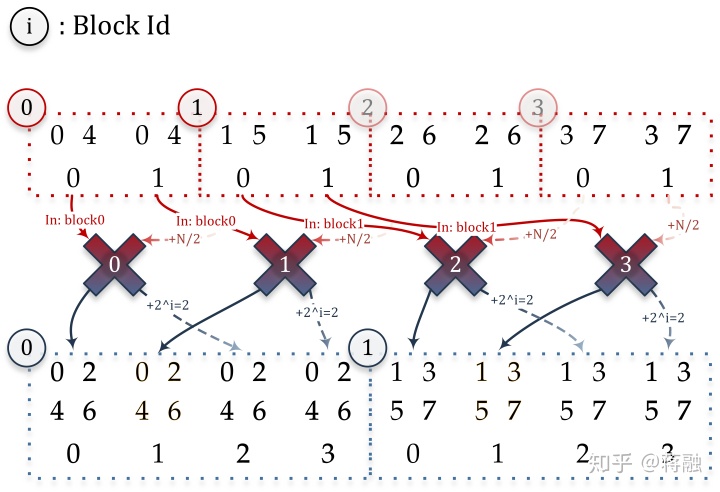
输出数据(波形)放在哪里, 这个问题稍微复杂一点; 先观察一下上图中输出下标的规律:

1. 拥有相同样本集合的一组波形, 都是按频率从小到大连续排列在一块(例子见图中绿虚线框);
2. 对于样本不同的两组波形块, 根据输出它们的蝶形变换的序号来从小到大排列; 小的一组排在左边, 大的一组则排到右边;
3. 把输入和输出波形按照样本集合进行分块; 可以观察到, 迭代次数为
   时, 输入波形块的大小为
   , 输出波形块的大小为
   ; 输入波形块
   组成一对, 里面的波形两两配对, 然后蝴蝶变换到输出波形块
   ;
4. 第
   个蝴蝶变换的输入和输出波形块:
5. 也就是说, 输出的一对波形数据必定在同一个输出波形块之内. 那这就好办了, 因为根据观察1, 同一个波形块内部是按照频率从小到大排序的; 第
   个蝴蝶变换输入波形的频率为
   
   那么根据蝴蝶变换公式, 输出波形的频率为
6. 也就是说, 对于每个蝴蝶变换的一对输出下标
   , 我们只需要考虑左边(较小)的那个下标
   , 而
   的位置由
   可推出:
7. 现在再来看较小的输出下标
   怎么算, 输出波形块的起始下标为
   在输出波形块内部的偏移(offset)为
   
   起始下标和偏移量加起来就是输出下标:

这里我从上图中截取第二次迭代作为例子:

理论部分就写到这里, 实现部分可能得过一阵子了... 事情太多.