一阶电路误差分析_PDE有限差分方法(12)——对流方程数值格式的分析方法

今天直接把张强书上的第6章大部分内容完成掉. 主要讲对流方程数值格式的相容性、稳定性以及数值振荡的分析方法。

参考书：
(1) J.W. Thomas - Numerical Partial Differential Equations_ Finite Difference Methods (1995, Springer)
(2) 张强《偏微分方程的有限差分方法》科学出版社，2019年1月版。
(3) K. W. Morton, D. F. Mayers - Numerical solution of partial differential equations (2005, Cambridge University Press)

今天内容：

1 五种差分格式的数值表现

考虑初值函数

同时具有光滑部分与间断部分, 比较迎风格式与LW格式的数值表现. （图来自张强书的插图）

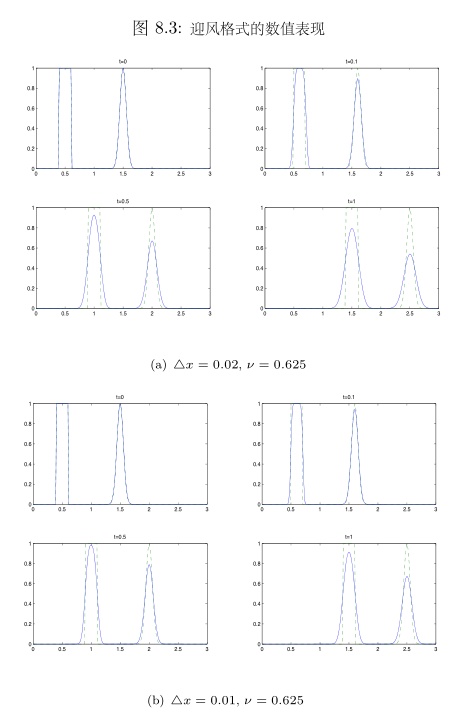
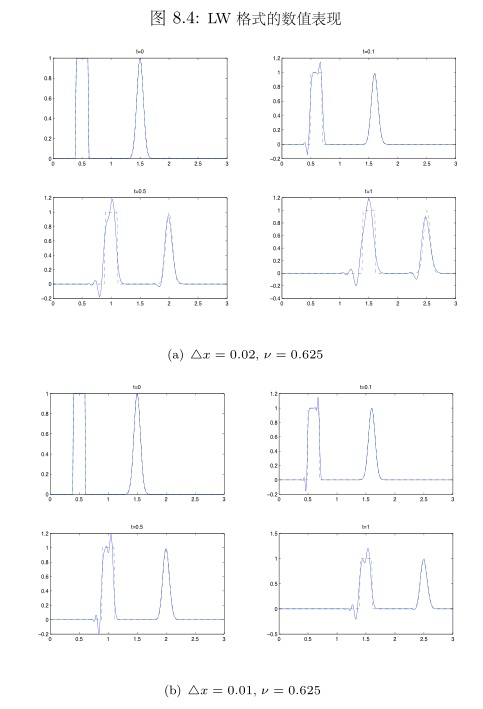
• 在真解光滑的区域, 两个格式的数值表现都比较理想, LW格式相容阶更高, 误差更小.
• 在间断界面附近, 迎风格式的间断界面(也叫数值过渡区域)是平滑的; 但LW格式出现了数值振荡与上下溢出. 即使加密网格也不会得到明显改善. (网格加密后, 数值震荡明显可见的时间仅仅是被推迟了, 不可能消除)
• 这个例子表明双曲方程的数值困难, 即高阶精度与数值振荡是无法调和的两个对立面.迎风格式与LW格式各有优缺点, 我们希望构造尽可能保持高阶精度且保持间断面的形态.

下面用Lax格式与迎风格式进行对比. 空间步长

网比

• 根据数值结果, 两个格式捕捉间断界面位置都比较精确. 但是在间断界面附近, Lax格式的数值过渡区域更宽, 峰值下降程度更厉害, 即Lax格式比迎风格式有更强的数值耗散机制.

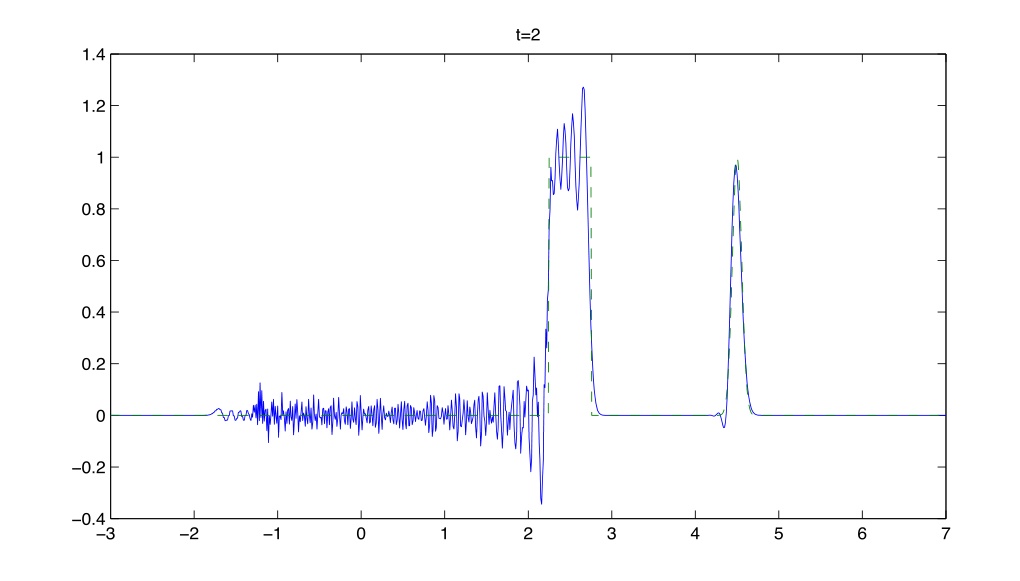
下面绘制蛙跳格式在不同时刻的数值解. 空间步长

网比

第一层初值采用LW格式设置(迎风格式类似).

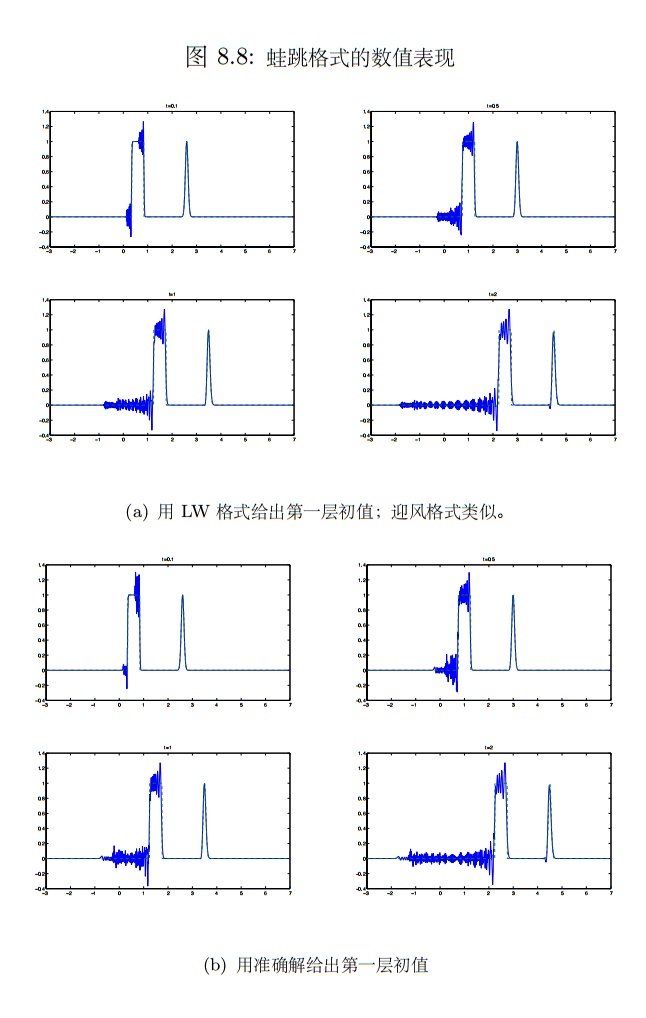
• 可以发现: 数值振荡出现在波后, 污染区域(振荡区域)随时间发展而变宽.

下面观察盒子格式的效果, 初值改为

空间步长

网比

可以发现, 数值振荡出现在波前, 污染区域随着时间发展而逐渐变宽.

2 线性常系数差分格式

考虑如下的线性常系数差分格式:

其中

是差分系数, 同格点位置与网格函数无关.

2.1 相容性

定理 差分方程

与对流方程

相容的充要条件是

若相容, 则局部截断误差至少为一阶.

证明：差分方程的局部截断误差是

由Taylor展开到二阶项即可证明结论. QED

由于对流方程有行波解结构, 差分方程

的相容阶有简便的判别方法: 若

均满足差分方程, 则局部截断误差至少达到k阶. 所以这个定理也可以改写为

函数1与

均精确满足差分方程, 则差分方程相容.

例 给出差分方程

达到k阶相容的充要条件.

由Taylor展开到k项,

由局部截断误差的定义,

如果要让格式是k阶相容的, 只需

化简得

2.2 单调格式与数值振荡

一个差分格式是单调保持格式指: 若数值初值单调, 则由这个差分格式得到的数值解也保持一定的单调性. (否则, 单调性刻画出现错误, 数值振荡随之产生. 所以单调保持性质是数值格式避免数值振荡的前提条件. )

单调格式指差分系数

非负.

注：由前面的相容性定理, 如果一个单调格式是相容格式, 则它具有凸组合的系数结构. 所以相容的单调格式满足离散最大模原理, 具有最大模稳定性! 也可以证明相容的单调格式有

$模稳定性, 后面将会介绍.

定理 单调格式也是单调保持格式, 反之亦然.

证明：用归纳法证明即可. 逆命题可以考虑用下面的反例证明: 如果数值格式有负系数, 不妨设

考虑初值

代入差分方程可得

数值解不再保持单增性质, 出现虚假数值振荡. QED

定理 [Godunov]单调格式至多具有一阶局部截断误差.

证明：设格式是相容的, 由Taylor展开, 局部截断误差为

$$

由Cauchy-Schwarz不等式与相容性条件,

等号成立的条件是

只有一个非零系数, 但这样的差分方程没有实际价值, 无需考虑.因此单调格式的局部截断误差至多一阶. QED

注：高阶相容的线性格式必定存在负系数, 数值振荡现象不可避免. 若要建立高阶无振荡格式, 需要跳出单调格式框架, 后面还会介绍TVD格式.

例1 LW格式、蛙跳格式、盒子格式都是高阶相容的, 不是单调格式, 由Godunov定理, 数值解会有数值振荡现象. 例2 迎风格式与Lax格式都是一阶相容, 在CFL条件下, 它们都是单调格式, 不会出现数值振荡.

2.3 数值耗散与数值色散

首先回顾一下Fourier方法. 对流方程

的

真解是

(模态解),其中

这个模态解的振幅(amplitude)是不衰减的(undamped)(即能量保持不变), 而一步时间推进以后, 相位(phase)增加了

对流方程的数值解形如

其中

是

的函数. 一步时间推进以后, 模态解会乘上振幅系数

它是复的.

的模长表示了这个格式是否稳定(数值耗散性质).

• 如果
  此时数值格式的振幅会膨胀, 出现反数值耗散性质, 则格式不稳定;
• 如果
  则模态解是衰减的(damped), 出现数值耗散现象.
• 如果
  则简谐波振幅保持不变, 此时格式是无耗散的.

把上面的

称为相位函数, k为波数,

为

相位速度,

为

波速. 若

则简谐波从左到右传播; 若

, 则简谐波从右到左传播.

把不同波数k的模态解(简谐波)叠加起来得到的整体波形就是原PDE的真解:

这里

是与

有关的常数:

它叫

色散关系(频散关系).

• 如果
  是线性函数, 则各个简谐波的波速
  相同, 所以整体的波形不变.
• 如果
  不是线性函数, 则不同波数
  的简谐波有不同的波速
  , 此时整体波形会发生变化, 这样的物理现象叫
  色散(频散), dispersion.

沿着波的传播方向, 位于波面(整体波形的波峰或者波谷或者间断界面)前面的位置叫波前, 位于波面后面的位置叫波后.

前面指出了, 增长因子的模

决定了数值格式的耗散性质(稳定性). 而增长因子的幅角

决定了数值色散性质.

数值解的相位与真解的相位的比为

其中

• 若
  则数值简谐波超前于真实简谐波;
• 若
  则数值简谐波滞后于真实简谐波.

通常数值相位速度

是非线性的, 不同波数

的数值简谐波有不同的波速

, 从而有数值色散现象.

注：数值色散现象会导致整体波形出现明显变化, 进而产生虚假的数值振荡现象, 如果

则数值振荡现象出现在波前; 如果

则数值振荡现象出现在波后.

注： 数值耗散与数值色散是导致数值误差的两个根本原因, 上述分析方法也适用于其他PDE的各种格式.

例1 LW格式的数值振荡出现在波后.

答: 设

足够小, 由Taylor展开,

所以数值解的相位与真解相位的比为

由于

足够小, 当

时, 数字1后面的误差项非正, 所以数值速度低于真实速度, 数值振荡出现在波后.

注：数值色散是数值振荡的根本原因, 数值耗散与数值色散的平衡关系决定数值振荡的具体表现.

例2 LW格式的增长因子满足

当

时, LW格式是有耗散的. 但是数值耗散的速度

比数值色散的速度

慢.

我们可以把前面涉及到的五种格式的

与

都写出来, 作一个总结:

• 迎风格式与Lax格式都有较强的数值耗散(耗散速度为
  ), 而LW格式有弱数值耗散(
  ). 蛙跳格式与盒子格式无数值耗散.
• 迎风格式和Lax格式是单调格式, 所以不会出现数值振荡现象. LW格式、蛙跳格式、盒子格式的阶数为2, 根据Godunov定理, 它们不是单调格式, 必定有数值振荡.
• 当
  时, LW格式、蛙跳格式的数值振荡出现在波后, 而盒子格式的数值振荡出现在波前. (当
  时相反)