数学猜想验证步骤_小数名师工作室 数学实验 || 包装箱的秘密

包装箱的秘密

--设计者简介--

   钱燕

   扬州市甘泉小学

   扬州市中青年教学骨干

实验视频

实验目的

由生活中的购物情境引出问题，再通过操作、计算、对比、演示等实验活动探索长方体在体积相等的情况下表面积的变化规律。从不同视角发现与理解长方体在体积相等的情况下怎样包装表面积最小，发展了学生的空间想象能力、推理能力，提升了学生的实践能力与创新意识。

实验工具

若干个1cm³小正方体、计算器等。

--实验过程--

超市里的物品琳琅满目，每样商品都需要包装，商家在设计包装箱时除了考虑美观，还想到要节省材料的问题。怎么包装最节省材料实际上就是数学上的求表面积最小的问题。今天，我们的数学实验就从研究包装箱的秘密开始。

研究复杂的问题，往往从简单开始。如果把1个棱长1cm的小正方体进行包装，方法只有1种。如果用这样的两个进行包装，方法也只有1种，这时拼成的大长方体的表面积变小，减少了重叠的这两个面。如果有这样的12个、24个呢？让我们一起开启今天的数学实验之旅吧!

实验活动一：

动手拼——提出猜想

同学们用12个棱长1cm的小正方体拼成不同形状的大长方体，看看一共有多少种不同的拼法？

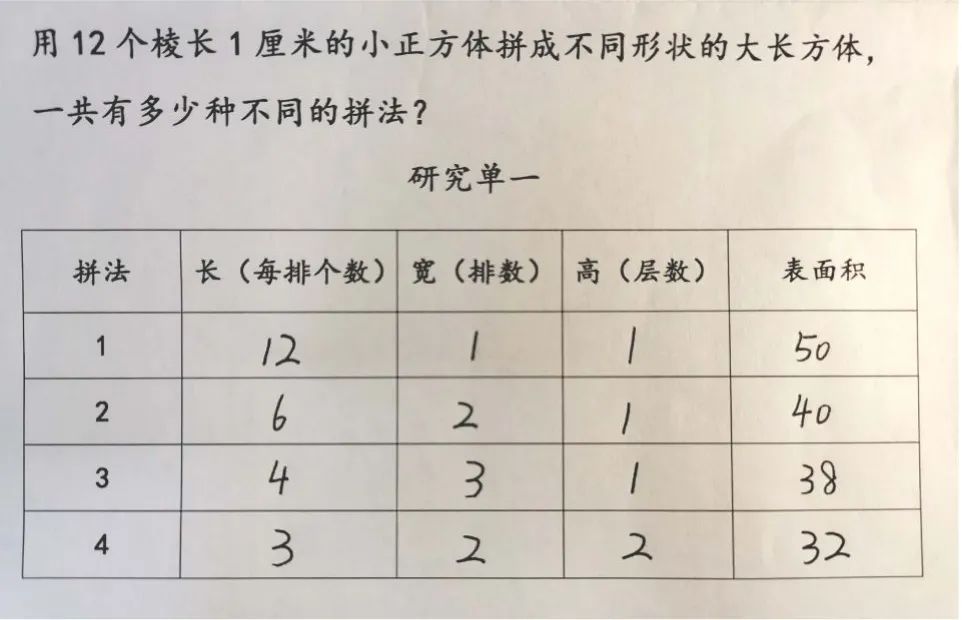
刚才我们把12个小正方体拼成了4种不同的长方体，仔细观察实验记录单，能发现什么呢？我们发现长方体的体积不变，当长、宽、高越来越最接近时，表面积就越来越小。是不是所有的长方体都这样呢？这只是我么的猜想，还需要进行验证。那怎样验证呢？我们可以借助多个正方体或长方体来拼成不同方体进行研究。

实验活动二：

想象拼——用正方体拼

同学们，如果让你能为24个棱长1cm的小正方体设计包装盒，怎样设计表面积最小呢？咱们可以在头脑中想象拼。为了有序列举出所有的拼法，可以从高1cm开始。

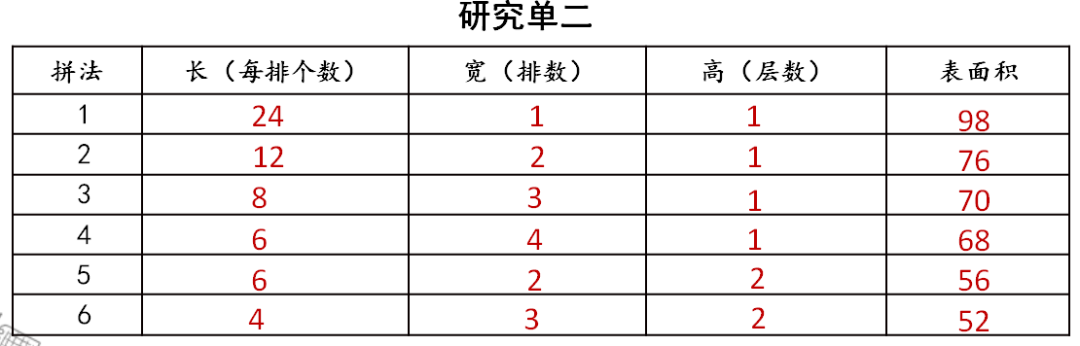
通过刚才的实验，我们发现体积不变的情况下，长4cm、宽3cm、高2cm的这种长方体表面积最小。

实验活动三：

想象拼——用长方体拼

接下来，咱们借助长方体进一步验证。

用两个完全相同的长方体来拼，怎样拼表面积最小？动脑筋想一想，可以上下重叠、左右重叠、前后重叠，不难看出，重叠的面积越大，拼成的长方体表面积越小。观察数据，也能清楚地发现：上下重叠时，高变了；左右重叠时，长变了；前后重叠时，宽变了。

对比刚才的三组数据，请观察表面积最小的情况，你有什么发现？

仔细观察刚才的三组实验数据，有力的验证我们的猜想是正确的。

得出结论：若干个完全相同的小正方体或小长方体拼成大长方体长方体体积不变，当长、宽、高越接近时，拼成的长方体的表面积越小。

回顾我们的研究过程，我们从生活中的问题入手，引发了猜想，通过实验验证，得出了结论。

--结语--

这样的研究思路在我们的数学学习中经常要用到。希望同学们在今后的学习中，善于思考，勇于探索，攀上数学的高峰。

图文｜钱   燕

制作｜朱奕璇

审核｜高   静