c++ 跳出函数_跳出三界外，还在五行中郑州二质检数学卷“秒杀”（课堂札记）...

      试卷评讲课堂实录

 删繁就简，躲避开计算

          --郑州二质检理科数学几个快捷“秒杀”

      刚考完的郑州二质检数学理科试卷，抛开出题有瑕疵的试题，那么，在考试中，想提高做题速度，则需要同学们通过一轮积累的一些知识和技巧，再加上“特殊值”大法，可以绕开一些不必要的计算量。

      二轮考试前后，可以开始积累一些快速技巧了。今天，一起研究一下这次考试中的那些试题可以找到快速技巧，借此来提高做题速度。

    本文解法，都是田老师试卷评讲课时与学生的课堂互动探讨，也包括脸红脖子粗的争吵，还包括一些开启群嘲模式，更有“哇，原来还可以这样”的惊叹，甚至还有让老师挠头继而赞不绝口的胡思乱想。

      总而言之，要把重要试卷的每一道题都要说一下，才是大考之后的试卷评讲课。

以下是一部分的课堂互动札记：

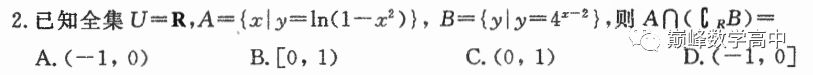
       A有 B没有！

      本题算不上节省计算量，不过，如果对于对数定义域和指数值域非常熟悉的话，知道指数值域大于零，补集必含零，0也是A的对数定义域，所以答案是D。

     类似这样的求集合的，特别是含有复杂的含有不等式运算的试题，都可以借此来代入“秒杀”。拿着四十五套金考卷，只看第一二位置的这类小题，很快就把这个位置的题练完。

      这道题，通过基础变换后得到函数2sin(1/2 x+30*)， 注意到周期是4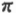。都可以代特制排除。

A:代人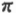可排除。

B：知x=-30*，函数值必须是0，可排除。

C:  X=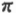/3,函数值也必须是0，可排除。

如果一轮讲的“快速画图法”运用的好，直接看出D答案正确。

当然，对称中心等知识熟练，也可以直接做出来。

       牢记“快速做图法”是解决三角函数小题的不二法宝。为此，晚上辅导课时候还抽查，甚至一个一个排查，要求每个人必须会快速画图。

      最特殊的就是2017年这道理科题，通过“起点画图”，基本上一两分钟就通过出图秒杀，箴言一句海清河晏嘛，根本不需要神马诱导公式化简的等等。

线性规划题，注意到不等式组和z的式子，都是对应的线型，所以直接解出交点代入即可。当然，这个题，也有很多不安定因素，最令人不安的就是，约束条件是否是封闭多边形，否则就容易出错。此类题反复强调，不建议用解交点值代入法做，尽量观察完图像再确定。

上边几题，应为都是比较容易的，下边从第七题开始，就逐渐有了“狂飙猛进”的做题速度、

实际上求最值，可以排除答案BC,不过，依然难以区分。有垂直，有长度，再不建系，天理不容嘛。P点显然在直线x+y=2上，设点写出坐标即可。如果基底与数量积的推导能力稍微差的同学，就没必要用基底推导了。

建系，设点，化为解析，是解决向量一些超麻烦试题的重要法宝之一。要牢牢记住“与形状局部或者完全无关”这个向量的拓扑学性质。当然，这个方法也偶尔会带来解析几何繁复的计算，心里要有数。

     这道题，正规方法用的是分离常数，再值域即可，这个方法也不算特别难。此处的快捷解法，源于第一轮复习，对于这个函数的认识和积累：

1、对称中心必在y轴上

2、那么对称中心在哪条轴上呢？

        有以上一轮积累可知，，现在可以排上用场了。首先有高斯函数定义，把答案A，B排除。再把x=-1代入，得到y=7/4，且极限判断法知y>1/2,右对称性知道最大值域小于3.所以排除含有3的D答案。

      当然，第一轮如果没有这个研究性积累的话，上边的判断犹如天书般费解，那还是老老实实的分离常数求值域吧。

        要注意，指对函数，如果式子复杂，但是里边可能蕴含着“对称轴和对称中心”这个特殊的意外之财！ 

        这类函数，还要求学生在课余，自己用田老师发的手机软件反复画图变化，加强印象。

这道题，是有问题的试题之一，具体详细解法，可参考如下。

       虽然有问题，但是咱们依然可以说它的快捷解法。

       注意到F2P/F1P=2a/C，显然这俩焦半径兄弟不会相等，必有大小关系，所以，令2a/C=1,得e=2，显然有对称性，必有在e=2左右两侧的值，这个答案在(1,2)子区间和(2，某个值)之内。

      不过是错题，所以等它修改后再秒杀吧。

       但是，本题第一个答案，确实有点太过分了，双曲线离心率不仅仅小于1，竟然还有负的，这，就有点太侮辱智商了吧。

       本题，如果说P点在右支上，那就不用问，把所有离心率小于2的，通通咔嚓咔嚓掉。

      圆锥曲线，做题要注意它的对称性，在离心率中起到了关于某个数的“对称”特性。

   这个只是一种经验，不能当做必要条件，否则死的很快。所以，好的出题老师，一般会把答案反复斟酌，消除这种明显的“特性”。

       这道题，显示逻辑分析的重要性。这个折叠图形，是源于中招试题的一个思维。根据题意，如果取极限位置，p点投影为M,则必有X

=BM

   当时，问孩子们，怎么能保证折叠一定在咱们这个讨论氛围之内，而不会更小？

有学生当时就不屑的把演草纸拿来开始折叠展示给我，吓得我赶紧承认这问题太幼稚了。

所以这个才是爽快淋漓的分析法，完全把繁琐的图像计算绕开了。

此题若果想要节省计算，需要补充抛物线焦点弦中点弦的一些二级甚至三级结论，如下图是本题用到的结论，所以没有那种快速计算的“惊艳”感觉。

       填空题，没有可供琢磨的选项，并且要求答案的完备性，所以，一般很难有快算结果，只有所谓快速思维罢了。如这一题

       如快速思维，也就是平常做题的常规思路：如果角复杂，要寻找拆角技巧。把试题中的角加加，减减，乘乘，除除，等等乱七八糟的构造寻觅。

       当然，本题“打撒了”再观察，也未尝不可。总而言之，这道题，出题老师终于手边放着《金刚经》来出题了，说明有了佛家慈悲之怀！

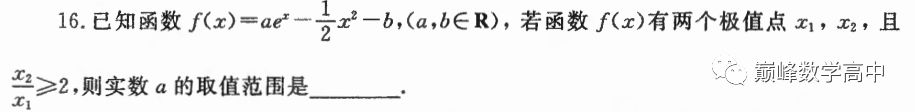
         由分离参数，可得

出图像，把x2/X1比值取等号，可得a的上界值。作为填空题，可以直接用极限法得到下界为a=0。后续计算，就是常规的解方程了。不在赘述。

         这一道题，实际上是一道21题位置的导数第二问大题改编的小题，具体小题大做的分析过程，可以参考这个视屏：

2019郑州二质检16题的一种解法：换元构造法

        大题，因为需要有过程，所以很难有可以省略的计算过程。不过，选做这道题的同学，一定要牢牢记住一轮复习时候，关于这个函数的总结：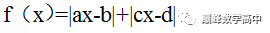

          这个图像最大的特征，是“开口向上”，则最小值必在“拐点处”，这样，心里就明镜似的，剩下只是书写过程而已。

    二质检以后，做题，就要开始“上帝视角”了，要跳出试题，远远的观察一下，是否有可供狂奔的蛛丝马迹。当然，平时有秒杀试题，做完，还得回过头来，搞清楚它的来龙去脉，积累知识。

   是谓“跳出三界外，还在五行中！” 

          二轮以后，开始进入上帝视角琢磨研判试题了！