easy_ECC

easy_ECC（来源：攻防世界）

1.关卡描述

---

2.解题步骤

---

分析：

根据公式来求解：

这个是真不会。

==================================

参考资料：

直接使用大佬脚本：（来自哪，当时忘记保存出处了）

import collections
import random
 
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
 
curve = EllipticCurve(
   'secp256k1',
   # Field characteristic.
   p=int(input('p=')),
   # Curve coefficients.
   a=int(input('a=')),
   b=int(input('b=')),
   # Base point.
   g=(int(input('Gx=')),
      int(input('Gy='))),
   # Subgroup order.
   n=int(input('k=')),
   # Subgroup cofactor.
   h=1,
)
 
 
# Modular arithmetic ##########################################################
 
def inverse_mod(k, p):
   """Returns the inverse of k modulo p.
  This function returns the only integer x such that (x * k) % p == 1.
  k must be non-zero and p must be a prime.
  """
   if k == 0:
       raise ZeroDivisionError('division by zero')
 
   if k < 0:
       # k ** -1 = p - (-k) ** -1 (mod p)
       return p - inverse_mod(-k, p)
 
   # Extended Euclidean algorithm.
   s, old_s = 0, 1
   t, old_t = 1, 0
   r, old_r = p, k
 
   while r != 0:
       quotient = old_r // r
       old_r, r = r, old_r - quotient * r
       old_s, s = s, old_s - quotient * s
       old_t, t = t, old_t - quotient * t
 
   gcd, x, y = old_r, old_s, old_t
 
   assert gcd == 1
   assert (k * x) % p == 1
 
   return x % p
 
 
# Functions that work on curve points #########################################
 
def is_on_curve(point):
   """Returns True if the given point lies on the elliptic curve."""
   if point is None:
       # None represents the point at infinity.
       return True
 
   x, y = point
 
   return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
 
 
def point_neg(point):
   """Returns -point."""
   assert is_on_curve(point)
 
   if point is None:
       # -0 = 0
       return None
 
   x, y = point
   result = (x, -y % curve.p)
 
   assert is_on_curve(result)
 
   return result
 
 
def point_add(point1, point2):
   """Returns the result of point1 + point2 according to the group law."""
   assert is_on_curve(point1)
   assert is_on_curve(point2)
 
   if point1 is None:
       # 0 + point2 = point2
       return point2
   if point2 is None:
       # point1 + 0 = point1
       return point1
 
   x1, y1 = point1
   x2, y2 = point2
 
   if x1 == x2 and y1 != y2:
       # point1 + (-point1) = 0
       return None
 
   if x1 == x2:
       # This is the case point1 == point2.
       m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
   else:
       # This is the case point1 != point2.
       m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
 
   x3 = m * m - x1 - x2
   y3 = y1 + m * (x3 - x1)
   result = (x3 % curve.p,
             -y3 % curve.p)
 
   assert is_on_curve(result)
 
   return result
 
 
def scalar_mult(k, point):
   """Returns k * point computed using the double and point_add algorithm."""
   assert is_on_curve(point)
 
 
 
   if k < 0:
       # k * point = -k * (-point)
       return scalar_mult(-k, point_neg(point))
 
   result = None
   addend = point
 
   while k:
       if k & 1:
           # Add.
           result = point_add(result, addend)
 
       # Double.
       addend = point_add(addend, addend)
 
       k >>= 1
 
   assert is_on_curve(result)
 
   return result
 
 
# Keypair generation and ECDHE ################################################
 
def make_keypair():
   """Generates a random private-public key pair."""
   private_key = curve.n
   public_key = scalar_mult(private_key, curve.g)
 
   return private_key, public_key
 
 
 
private_key, public_key = make_keypair()
print("private key:", hex(private_key))
print("public key: (0x{:x}, 0x{:x})".format(*public_key))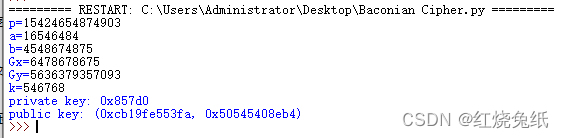

public key: (0xcb19fe553fa, 0x50545408eb4)

再16进制转10进制可得

题目要求答案是x+y所以得出答案为

cyberpeace{19477226185390}

方法二：

利用工具ECCTOOL解题

首先我们选择数据为十进制，其次椭圆曲线类型为G§，接着输入a、b、p还有下面的GX,GY以及k后，点击CALC R即可得到RX,RY,然后相加就得到答案了。

rx = 13957031351290

ry = 5520194834100

rx + ry = 19477226185390

下载链接：https://bbs.pediy.com/thread-66683.htm

 ECC相关原理

一般情况下，椭圆曲线可用下列方程式来表示，其中a,b,c,d为系数。

椭圆曲线基础理解：

E:y2=ax3+ bx2+cx+d加法

过曲线上的两点A、B画一条直线，找到直线与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A+B，即为加法。如下图所示：A + B = C

二倍运算

上述方法无法解释A + A，即两点重合的情况。因此在这种情况下，将椭圆曲线在A点的切线，与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A + A，即2A，即为二倍运算。

椭圆曲线加密：

假设椭圆曲线为y² = x³ + x + 1，其在有限域GF(23)上时，写作：　　y² ≡ x³ + x + 1 (mod 23)

此时，椭圆曲线不再是一条光滑曲线，而是一些不连续的点，如下图所示。以点(1,7)为例，7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此还有如下点：

(0,1) (0,22)　　(1,7) (1,16)　　(3,10) (3,13)　　(4,0)　　(5,4) (5,19)　　(6,4) (6,19)　　(7,11) (7,12)　　(9,7) (9,16)　　(11,3) (11,20)　　等等。

另外，如果P(x,y)为椭圆曲线上的点，则-P即(x,-y)也为椭圆曲线上的点。如点P(0,1)，-P=(0,-1)=(0,22)也为椭圆曲线上的点。

考虑K=kG ，其中K、G为椭圆曲线Ep(a,b)上的点，n为G的阶（nG=O∞ ），k为小于n的整数。则给定k和G，根据加法法则，计算K很容易但反过来，给定K和G，求k就非常困难。因为实际使用中的ECC原则上把p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据

点G称为基点（base point）

k（k）为私有密钥（privte key）

K为公开密钥（public key)

公钥加密：选择随机数r，将消息M生成密文C，该密文是一个点对，即：C = {rG, M+rK}，其中K为公钥

私钥解密：M + rK - k(rG) = M + r(kG) - k(rG) = M　　其中k、K分别为私钥、公钥。