四个角不是直角的四边形_(九上)期中复习专题一：平行四边形与特殊平行四边形...

下载地址：九上期中复习专题一：平行四边形与特殊平行四边形

九上复习专题一：平行四边形与特殊平行四边形(一)

【知识点1】

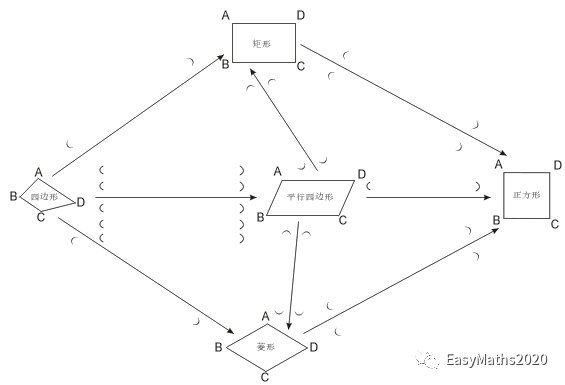一般平行四边形与特殊平行四边形的关系(请在括号内填写相关的判定条件)

几种平行四边形的性质比较(矩形、菱形、正方形只需填写不同于平行四边形的性质即可)

图形	边	角	对角线	对称性	对称中心/对称轴

【知识训练1】

1．四边形ABCD中，∠A=50°，欲使四边形为平行四边形，则∠B=____ _，∠C=__  __，∠D=__  __．

2．如图，在平行四边形ABCD中，已知对角线AC和BD相交于点O，

△ABO的周长为17，AB＝6，那么对角线AC＋BD＝           ．

3.在矩形ABCD中，AC、BD相交于点O，∠AOB= 60°，AB=6，则AC=_______           第2题图

4.已知矩形的周长是24，相邻两边之比是1：2，那么这个矩形的面积是__________

5.矩形的两条对角线所形成的的锐角为60°，一条对角线与短边的和为15，则短边长为_________

6.在菱形ABCD中，对角巷相交于点O， OA=8，OB=6，则菱形的周长是_________，面积是___________

7.菱形的一个内角为120°，较短的对角线长为10，那么菱形的周长是_____________

8.菱形的对角线长为10和24，则周长为_________。

9.正方形ABCD中，E为BC上一点，且EF⊥BD于F,  那么 △EFB是___________三角形。

10．如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，

在对角线AC上有一点P，使PD+PE最小，则这个最小值为 (      )

   A．        B．        C．                 D．                   第10题图

【知识点2】三角形中位线定理.直角三角形相关定理

1. 三角形的中位线定理:三角形的中位线平行于__________________，并且等于____________________。

2．直角三角形斜边上的中线等于________ ____，直角三角形中30^o角所对的直角边等于斜边的_   ___．

【知识训练2】

11．直角三角形两条直角边的长分别为12和5，则斜边上的中线长为(    )

A.26      B.13       C.8.5        D.6.5

12．如图，在四边形ABCD中，AD平行于BC，AD=6cm，BD=9cm，AB=CD=8cm，E.F.G.H分别是AD 、BD、BC、AC的中点，那么四边形EFGH的周长是(     )

   A.14cm     B.15cm     C.16cm     D.17cm

13．如图，在矩形ABCD中，P、R分别是BC和DC上的点，E、F分别是AP和RP的中点，当点P在BC上从点B向点C移动，而点R不动时，下列结论正确的是(　  　)

A．线段EF的长逐渐增长        B．线段EF的长逐渐减小

C．线段EF的长始终不变      D．线段EF的长与点P的位置有关

14．如图，四边形ABCD中，∠A=90°，AB=，AD=3，点M，N分别为线段BC，AB上的动点(含端点，但点M不与点B重合)，点E，F分别为DM，MN的中点，则EF长度的最大值为(　  　)

A．3                 B．4               C．4.5                 D．5

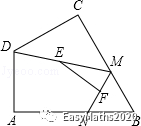
  第12题图                  第13题图                  第14题图               第15题图

15．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为12cm²，则S_△DGF的值为(　　  )

A．4cm²             B．6cm²         C．8cm²                  D．9cm²

16．如图，在△ABC中，D是BC上一点，AB=AD，E、F分别是AC、BD的中点，EF=2，则AC的长是(　　)

A．3             B．4                 C．5                 D．6

17．如图，在平面直角坐标系中，点O为坐标原点，△ABC是边长为16 的等边三角形，点A、B分别在x轴的正半轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则线段OC的长的最大值是　   　．

18．如图，在△ABC中，AB=AC=7，BC=6，AF⊥BC于F，BE⊥AC于E，D是AB的中点，则△DEF的周长是　   　．

19．如图，△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，若∠A=50°，则∠FME的度数　   　．

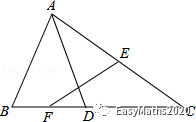
     第 16题图                    第17题图                      第18题图                第19题图

【典型例题】

20．如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．

(1)求证：BE=DF；

(2)若 M.N分别为边AD.BC上的点，且DM=BN，试判断四边形MENF的形状．

21．如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE.求证：OE=BC．

22．在△ABC中，BE、CF分别为边AC、AB上的高，M为BC的中点，MN⊥EF于点N．求证：FN=EN．

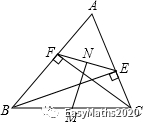
23．如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证AE=EF.

九上复习专题一：平行四边形与特殊平行四边形(二)

【例题剖析】

例1．下列命题中，真命题是(      )

A.有两边相等的平行四边形是菱形      B.有一个角是直角的四边形是矩形

C.四个角相等的菱形是正方形         D.两条对角线互相垂直且相等的四边形是正方形

例2．如图1，ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长(    )

A.4 cm       B.6cm      C.8cm        D.10cm

例3．如图2，已知正方形ABCD的边长为1，连结AC、BD,CE平分∠ACD交BD于点E,则DE=          。

 

     图1                       图2                     图3                   图4

例4．如图3，正方形的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为　   　．

例5．如图4，过矩形对角线AC的中点O作EFAC分别交AB，DC于E、F，点G为AE的中点，若∠AOG=30°，AB=6，则　      　． 

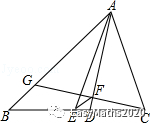例6．如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，求线段EF的长．

【基础练习】

1．在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是(      )

A．AB=BC=CD=DA                     B．AC⊥BD，AC=BD     

C．AO=BO=CO=DO，AC⊥BD           D．∠A=∠B=∠C=∠D

2．在ABCD中，∠A：∠B：∠C：∠D的值可以是(    )

A.1：2：3：4     B.1：2：2：1     C.2：2：1：1      D.2：1：2：1

3．用两块完全相同的直角三角形拼下列图形：①平行四边形  ②矩形  ③菱形  ④正方形 ⑤等腰三角形  ⑥等边三角形，一定能拼成的图形是(    )

A.①④⑤     B.②⑤⑥     C.①②③    D.①②⑤

4．如图，在ABCD中，已知AD＝8cm，AB＝6cm，DE平分∠ADC交BC边于点E，则BE等于(    )

A.2cm                 B.4cm             C.6cm                D.8cm

第4题图                  第5题图                   第6题图                第7题图          

5．如图，在四边形ABCD中，E是BC边的中点，连结DE并延长，交AB的延长线于F点，．添加一个条件，使四边形ABCD是平行四边形．你认为下面四个条件中可选择的是(    )

A.           B.              C.              D.

6．如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF．

则∠CDF等于(    )   A.80°     B.70°     C.65°       D.60°

7．如图，点M是ABCD的边AD上任意一点，则S，则(   )

A. 8cm²        B. 10cm²      C. 12cm²          D. 16cm²

8．如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：

①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④．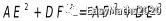

其中正确的是(     )

A．②③   B． ②④     C．①③④    D．②③④

            第8题图                                    第9题图                 第10题图      

9．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是1和2，则正方形的边长是       ．

10．如图，在矩形ABCD中，点E、F分别在AB、DC上，BF∥DE，若AD=12cm，AB=7cm，

且AE：EB=5：2，则阴影部分的面积为_______cm

11．已知菱形的两条对角线的长分别是6和8，那么它的边长是__    _____．

12．正方形的对角线的长与它的边长的比            ．

13．如图，CD与BE互相垂直平分，AD⊥DB,∠BDE=70⁰，则∠CAD=        ⁰．

                                                                                         第13题图

14．如图，在平行四边形ABCD中，E，F分别是AC，CA延长线上的点，且CE=AF，则BF与DE具有怎么样的关系？试说明理由

15．如图，点M，N分别在平行四边形ABCD的边BC，AD上，且BM=DN，，，垂足分别为E，F，求证：MN与EF互相平分

16．如图，已知点E，F分别是ABCD的边BC，AD上的中点，且∠BAC=90°．

(1)求证：四边形AECF是菱形；

(2)若∠B=30°，BC=10，求菱形AECF面积．

17．阅读材料并解答问题

如图①，以Rt△ABC的直角边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，可以得出结论△ABC的面积与△AEG的面积相等．

(1)在图①中的△ABC的直角边AB上任取一点H，连接CH，以BH、HC为边分别向外作正方形HBDE和正方形HCFG，连接EG，得到图②，则△HBC的面积与△HEG的面积的大小关系为　      　．

(2)如图③，若图形总面积是，其中五个正方形的面积和是，则图中阴影部分的面积是　      　．

(3)如图④，点A、B、C、D、E都在同一直线上，四边形X、Y、Z都是正方形，若图形总面积是，正方形Y的面积是，则图中阴影部分的面积是　      　．

18．如图，已知在△ABC中，AC=6，BC=8，AB=10，点P是AB上 (不与A、B重合)，过P作PE⊥AC，PF⊥BC，垂足分别是E、F，连结EF，M为EF的中点．

(1)请判断四边形PECF的形状，并说明理由；

(2)随着P点在边AB上位置的改变，CM的长度是否也会改变？若不变，请你求CM的长度；若有变化，请你求CM的变化范围．