马尔科夫链是一种时间离散的随机过程。因为时间是离散的,所以我们可以用整数
这个矩阵
马尔科夫链的一个特征是无记忆性,也就是马尔科夫链的演化只依赖于当前状态,而不依赖于过去的历史。现实世界中很多过程都可以简化为一个马尔科夫链。一个例子就是一维的随机游走。假设有一个被限制在一维空间的粒子,这个粒子每次以概率
第一节:一个简单的马尔科夫链
我们很有可能在高中时就已经接触到马尔科夫链了。这里有一道高中数学问题:
某城市有两个超市,分别记作A和B. 每次去A超市的人有20%下次仍然去A超市,其余的80%去B超市;每次去B超市的人有40%下次仍然去B超市,其余的60%去A超市。请问,经过足够长的时间后,去这A超市的人口和去B超市的人数比例会不会趋近于一个常数?如果会,请问这个常数为多少?
我们可以记第
用矩阵表示为
这里得到了一个转移矩阵
使用递归,很容易得到
这是一个简单的马尔科夫链。对于每一个
这里已经涉及到了马尔科夫矩阵的一个重要性质,就是该矩阵的每一列的元素求和都是1. 因此,马尔科夫矩阵满足这个条件:
其中,
于是我们得到了矩阵
其中
马尔科夫矩阵的
当幂为无穷大的时候,我们得到
所以经过足够长的时间后,去A超市的人数趋近于
第二节:马尔科夫矩阵
上一节已经引入了马尔科夫矩阵,并用这个矩阵求解了一个简单的马尔科夫链问题。这一节里,我要将上一节的内容系统化。因为马尔科夫矩阵表示了状态间的转移概率,所以马尔科夫矩阵的每一个元素都应该是非负的。记马尔科夫矩阵元素为
这个性质决定了马尔科夫矩阵一定有一个值为1的特征值。而且可以根据 Gershgorin circle theorem 得到马尔科夫矩阵的任意一个特征值的绝对值都不可能大于一。为了得到马尔科夫矩阵的稳态解,我们需要计算马尔科夫矩阵的幂。当幂次为无穷大时,如果得到的矩阵是收敛的话,我们就把得到的矩阵称作是马尔科夫链的稳态矩阵。如果马尔科夫矩阵只有一个绝对值等于1的特征值,那么得到的幂矩阵一定是收敛的。相反,如果马尔科夫矩阵还有其它绝对值等于1的特征值,那么这个马尔科夫链就没有稳态解。通过幂矩阵的方法计算马尔科夫链稳态解的方法叫做power iteration method. Power iteration - Wikipedia 这个方法其实就是在计算马尔科夫矩阵特征值为1所对应的特征向量,该特征向量又叫做 Perron-Frobenius 向量。记
假设
所以稳态向量
Power iteration method 为,对于一个可对角化的矩阵
实际用这个算法计算特征向量的时候,我们需要先选取一个任意非零的初始向量
import numpy as np
def power_iteration(A):
(row, col) = A.shape
assert(row == col)
dimension = row
v = np.random.rand(dimension)
counter = 0
iteration_max = 1000
eps = 1.0e-15
while(counter < iteration_max):
counter += 1
v_updated = A.dot(v)
v_updated = v_updated/np.linalg.norm(v_updated)
error = min(np.linalg.norm(v - v_updated), np.linalg.norm(v + v_updated))
print "counter = " + str(counter) + ", error = " + str(error)
if (error < eps):
break
v = v_updated
eigenvalue = v_updated.dot(A).dot(v_updated)/v_updated.dot(v_updated)
return (eigenvalue, v_updated)经过测试,该算法可以给出正确的最大特征值和它所对应的特征向量。测试代码如下:
import numpy as np
def generate_matrix(dimension):
assert(dimension >= 2)
A = np.zeros((dimension, dimension))
for i in range(dimension):
for j in range(dimension):
A[i, j] = np.random.uniform()
return A
def find_leading_eig(A):
(eigenvalues, eigenvectors) = np.linalg.eig(A)
leading_eigenvalue = abs(eigenvalues[0])
leading_index = 0
for i in range(1, len(eigenvalues)):
if (leading_eigenvalue < abs(eigenvalues[i])):
leading_index = i
leading_eigenvalue = abs(eigenvalues[i])
return (eigenvalues[leading_index], eigenvectors[:, leading_index])
def is_proportional(a, b):
assert(len(a) == len(b))
eps = 1.0e-15
norm_a = np.linalg.norm(a, 1)
norm_b = np.linalg.norm(b, 1)
if (norm_a < eps and norm_b < eps):
return True
if (norm_a * norm_b < eps):
return False
a_normalized = a/norm_a
b_normalized = b/norm_b
#print ", ".join(map(str, a_normalized))
#print ", ".join(map(str, b_normalized))
error = min(np.linalg.norm(a_normalized - b_normalized), np.linalg.norm(a_normalized + b_normalized))
print "Difference of two leading eigenvectors = " + str(error)
if error < eps:
return True
return False
def main():
import sys
if (len(sys.argv) != 2):
print "dimension = sys.argv[1]. "
return -1
dimension = int(sys.argv[1])
A = generate_matrix(dimension)
(eigenvalue, eigenvector) = power_iteration(A)
print "leading eigenvalue = " + str(eigenvalue)
print "leading eigenvector = "
print eigenvector
(leading_eigenvalue, leading_eigenvector) = find_leading_eig(A)
print leading_eigenvalue
print leading_eigenvector
print "eigenvalue error = " + str(abs(eigenvalue - leading_eigenvalue))
print "consistent leading eigenvector? " + str(is_proportional(eigenvector, leading_eigenvector))
return 0
if __name__ == "__main__":
import sys
sys.exit(main())使用这个算法计算矩阵的最大特征值有它的局限性。为了知道它的局限性,我们首先需要知道这个算法为什么成立。对于一个可对角化的
其中
其中
对于任意的特征值,我们都有
这里,
在推导这个算法的时候,我们做了两个假设.
- 假设一:矩阵
是可对角化的。
- 假设二:矩阵
的绝对值为最大的特征值是唯一的。
这两个假设未必成立。有的矩阵是不可对角化的。不可对角化的矩阵称作是defective matrix. 对于不可对角化的
其中
对于马尔科夫矩阵,我们已经知道它最大的特征值为1,其余的特征值的绝对值要么小于1,要么等于1. 如果我们假设马尔科夫矩阵绝对值等于1的特征值的只有一个,那么我们就可以用power iteration method去计算它的特征向量。因为我们知道
一种特殊的马尔科夫矩阵是对称马尔科夫矩阵。对称马尔科夫矩阵的所有列的和与所有行的和都是1,因此
第三节:PageRank算法
PageRank算法最早被Google用来做网页排序。这个算法在很多领域都有着广泛的应用。我们可以将网页看作是一个有向图,图的节点是网页,如果网页A有一个链接指向网页B,那么在节点A和节点B之间我们就可以建立一条有向边。Google最开始试图发明一种算法,该算法可以给所有的网页按照重要度排序。直觉上,我们可以认为如果一个网页被很多网页链接,那么这个网页应该比较重要。如果一个网页被另一个重要的网页链接了,那么这个被链接的网页也应该比较重要。PageRank算法通过分析网页之间的关联来给网页排序。这个算法仅仅分析网页之间的关联,而不考虑网页的内容,因此也有一定的局限性。接下来,我要简单的介绍一下这个算法。我们很容易发现,这个算法本质上就是马尔科夫链的应用。
假设我们有如下的几个网页:
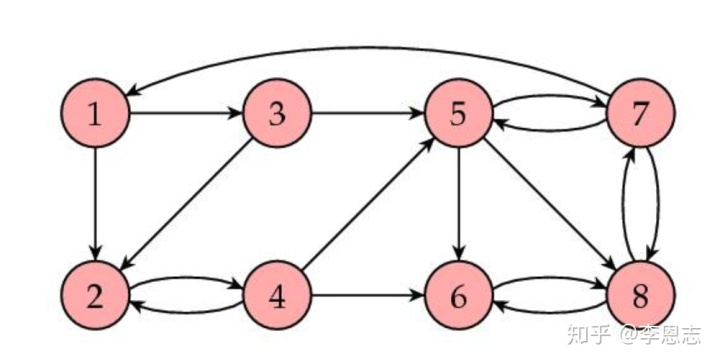
这些网页彼此之间有关联。例如网页1有链接指向网页2, 3,而网页1本身又被网页7指向。图中一共有8个节点,代表8个网页,我们的目标是通过分析网页之间的关联,来给每一个网页赋予一个重要度。记这个重要度为向量
其中
该矩阵元素
如果转移矩阵只有一个绝对值为1的特征值,那么这个马尔科夫链有稳态解,并且该稳态解是马尔科夫矩阵等于1的特征值所对应的特征向量:
数值上,稳态解可以通过递归关系
由此得到网页8的重要度最高,这与我们的直觉相一致。
这里我们假设了每一个网页都有指向其他网页的外部链接,但是实际上可能存在某些网页没有外部链接,这时得到的转移矩阵就不再是马尔科夫矩阵, 因为该转移矩阵存在某些和等于

第四节:代数图论
代数图论使用代数的方法研究图论。上一节的PageRank算法就是代数图论的一个具体应用。代数图论研究的内容远不限于上一节所示的有向图,也不限于仅仅是给节点的重要度排序。这里,我要系统地总结一下代数图论,并且将代数图论应用到更广泛的场景中。有空再写。也可以另外开辟一个专题讲这些内容。




















 527
527











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








