以下内容基本为转载内容,原文会在文末给出。
分支界限法,类似于回溯法,是一种在问题的解空间树T上搜索问题解的算法,在一般情况下,分支界限法和回溯法求解目标不同。回溯法求解目标是找出T中满足约束条件的所有解,而分支界限法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
分支搜索算法
所谓“分支”就是采用广度优先(BFS)的策略,依次搜索E-结点的所有分支,也就是所有相邻的结点,抛弃不满足约束的结点,其余节点加入活结点表。然后从表中选择一个结点作为下一个E-结点,继续搜索。
选择下一个E-结点的方式不同,则会有几种不同的分支搜索方式:
1.FIFO搜索;2.LIFO搜索;优先队列式搜索
分支界限法的一般过程
由于求解目标不同,导致分支界限法与回溯法在解空间树T上的搜索方式也不相同。回溯法以深度优先的方式搜索解空间树T,而分支界限法则以广度优先或以最小耗费优先的方式搜索解空间树T:
搜索策略
在扩展结点处,先生成所有的子结点(分支),然后从当前的活结点表中选择下一个扩展结点。为了有效的选择下一个扩展结点,以加速搜索的进程,在每一活结点处,计算一个函数值(限界),并根据这些已经计算出的函数值,从当前活结点表中选择一个最有利的结点作为扩展结点,使搜索朝着解空间树上有最优解的分支推进,以便尽快找出一个最优解。
分支界限法以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。问题的解空间树是表示问题解空间的一棵有序树,常见的有子集树和排列树。在搜索问题的解空间树时,分支限界法与回溯法对当前扩展结点所使用的扩展方式不同。在分支限界法中,每一个活结点只有一次机会称为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有子结点。在这些子结点中,那些导致不可行解或导致非最优解的子结点被舍弃,其余子结点被加入活结点中。此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所求的解或活结点表为空时为止。
对某个节点进行搜索时,先估算出目标的解,再确定是否向下搜索(选择最小损耗的结点进行搜索)在分支结点上,预先分别估算沿着它的各个儿子结点向下搜索的路径中,目标函数可能取得的界,然后把它的这些儿子结点和它们可能取得的界保存在一张结点表中,再从表中选择界最小或最大的结点向下搜索。一般采用优先队列维护这张表。
回溯法和分支界限法的区别
回溯法
1)(求解目标)回溯法的求解目标是找出解空间中满足约束条件的一个解或所有解。
2)(搜索方式深度优先)回溯法会搜索整个解空间,当不满条件时,丢弃,继续搜索下一个儿子结点,如果所有儿子结点都不满足,向上回溯到它的父节点。
分支限界法
1)(求解目标)分支限界法的目标一般是在满足约束条件的解中找出在某种意义下的最优解,也有找出满足约束条件的一个解。
2)(搜索方式)分支限界法以广度优先或以最小损耗优先的方式搜索解空间。
3)常见的两种分支界限法
a.队列式(FIFO)分支界限法(广度优先):按照队列先进先出原则选取下一个结点为扩展结点
b.优先队列式分支限界法(最小损耗优先):按照优先队列规定的优先级选取优先级最高的结点成为当前扩展结点
分支界限法步骤
假定源顶点为s,目标顶点为t。
- step1.初始化。建立根节点X
X.u = s
X.k = 1
X.path[0] = s
X.d = 0
X.b = 0
当前可行解的最短路径下界bound置位∞。 - step2.令顶点X.u所对应的顶点为u,对u的所有邻接顶点vi,建立儿子结点Yi,把结点X的数据复制到结点Yi
- step3.计算Yi的相关值
Yi.u = vi
Yi.path[Yi.k] = vi
Yi.k = Yi.k + 1
Yi.d = Yi.d + cu,vi
计算h和Yi.b - step4.若Yi.b < bound,转向step5;
否则剪去结点Yi,转向step6 - step5.把结点Yi插入优先队列。如果结点Yi.u = t,表明它是问题的一个可行解,用Yi.b更新当前可行解的最短路径长度下界bound。
- step6.取下优先队列首元素作为子树的根节点X,若X.u = t,表明它是问题的最优解,算法结束,数组X.path存放从源点s到目标顶点t的最短路径上的顶点编号,X.d存放该路径长度,否则,转向step2.
举个例子
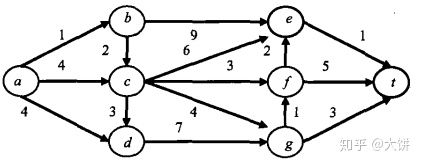
- k=1。
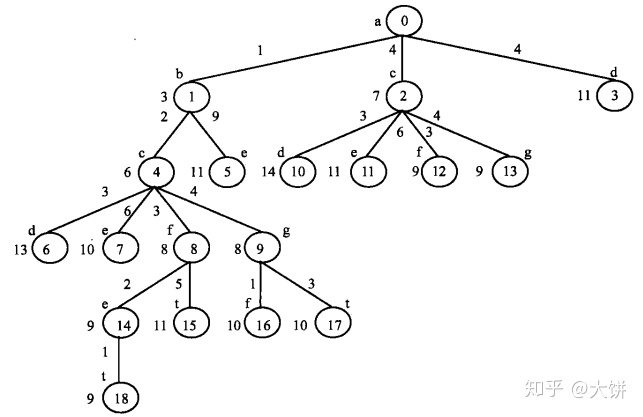
根节点0对应于源点a,有3个邻接顶点b、c、d,其下界为3,7,11,压入优先队列。 - k=2。优先队列中下界3最小,对于的顶点b,也即结点1。从顶点b继续进行搜索。
顶点b的邻接顶点为c和e,其下界为6和11,压入优先队列 - k=3。优先队列中下界6最小,对应顶点c,也即结点4.从顶点c继续进行搜索。
顶点c邻接顶点d、e、f、g,对应的下界为13,10,8,8,压入优先队列。(回溯到了k=2)k=2。优先队列中7最小,对应顶点c,也即结点2。从顶点c进行搜索。顶点c邻接顶点d、e、f、g,对应的下界为14,11,9,9,压入优先队列。 - k=4。优先队列中8最小,对应顶点f,也即结点8。
顶点f的邻接顶点为e、t,下界分别为9、11,压入栈中。其中11为一个可行解,将bound置为11. - (回溯到了k=4)k=4。优先队列中8最小,对应顶点g,也即结点9。
顶点g的邻接顶点为f、t,下界都是10。其中10为一个可行解,将bound置为10. - k=5.优先队列中9最小,对应顶点e,也即结点14.
顶点e只有一个邻接顶点t,下界为9,从而得到一个可行解,路径长度为9,加入优先队列中。
优先队列中最小的为9,且最后一个结点为t,因此是最优解。
背包问题
假定n个商品重量分别为w0, w1, ..., wn-1,价值分别为p0, p1, ..., pn-1,背包载重量为M。怎样选择商品组合,使得价值最高?
分支限界法解决背包问题
- 按价值重量比 递减 的顺序,对n个商品进行排序
排序后商品序号的集合为S = {0, 1, ..., n-1} - 将这些商品分为3个集合:
S1——选择装入背包的商品集合
S2——不选择装入背包的商品集合
S3——尚待选择的商品集合 - S1(k)、S2(k)、S3(k)分别表示在搜索深度为k时的3个集合中的商品。开始时有:
S1(0) = ∅;S2(0) = ∅;S3(0) = {0, 1, ..., n-1}
分支方法(二叉分支)
假设比值pi/wi最大的商品序号为s(s ∈ S3),用s进行分支,一个分支结点表示把商品s装入背包,另一个分支结点表示不把商品s装入背包。
当商品按照价值重量比递减排序后,s就是集合S3(k)中的第一个元素。特别地,当搜索深度为k时,商品s的序号就是集合S中的元素k。把商品s装入背包的分支结点
S1(k+1) = S1(k) ∪ {k}
S2(k+1) = S2(k)
S3(k+1) = S3(k) - {k}不把商品s装入背包的分支结点
S1(k+1) = S1(k)
S2(k+1) = S2(k) ∪ {k}
S3(k+1) = S3(k) - {k}
上界估算方法(贪心)
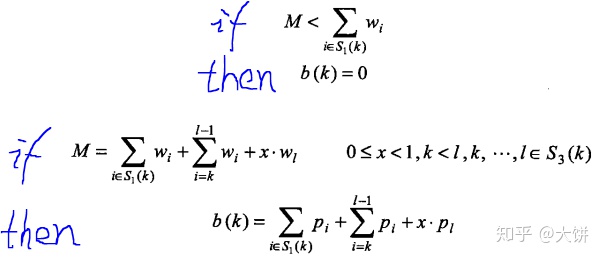
上述公式的理解
1)按照一个商品是否加入到S1集合,总共有2n个叶子节点,每个叶子节点对应一种情况
2)当一层一层向下搜索是,如果当前S1集合中的总重量超过了载重量M,则直接将b(k)置为0,该分支终止。为什么这样做?因为在搜索上一层时,该商品不应该加入到S1集合,这种不加入该商品情况对应于另一个分支。加入该商品的此分支已经不满足要求了,所以剪枝。
分支限界法求解步骤
每个结点都包含如下信息:
S1——当前选择装入背包的商品集合
S2——当前不选择装入背包的商品集合
S3——当前尚待选择的商品集合
k——搜索深度
b——上界bound——一个可行解的取值,当做剪枝的标准
- step1.bound = 0,把商品按价值重量比递减排序
- step2.建立根节点X
X.b = 0
X.k = 0
X.S1 = ∅
X.S2 = ∅
X.S3 = S - step3. 若X.k == n,算法结束,X.S1即为装入背包中的物体,X.b即为装入背包中物体的最大价值;
否则转向step4 - (分支1)step4.建立结点Y
Y.S1 = X.S1 ∪ {X.k}
Y.S2 = X.S2
Y.S3 = X.S3 - {X.k}
Y.k = X.k + 1
计算Y.b,将Y.b与bound进行比较,据此判定是否插入优先队列;当S3为空时,找到一个可行解,判定是否更新bound。 - (分支2)step5.建立结点Z
Z.S1 = X.S1
Z.S2 = X.S2 ∪ {X.k}
Z.S3 = X.S3 - {X.k}
Z.k = Z.k + 1
计算Z.b,将Z.b与bound进行比较,据此判定是否插入优先队列;当S3为空时,找到一个可行解,判定是否更新bound。 - step6.取出优先队列首元素作为结点X,转向step3
给出一个示例
有5个商品,重量分别为8,16,21,17,12,价值分别为8,14,16,11,7,背包的载重量为37,求装入背包的商品及其价值。
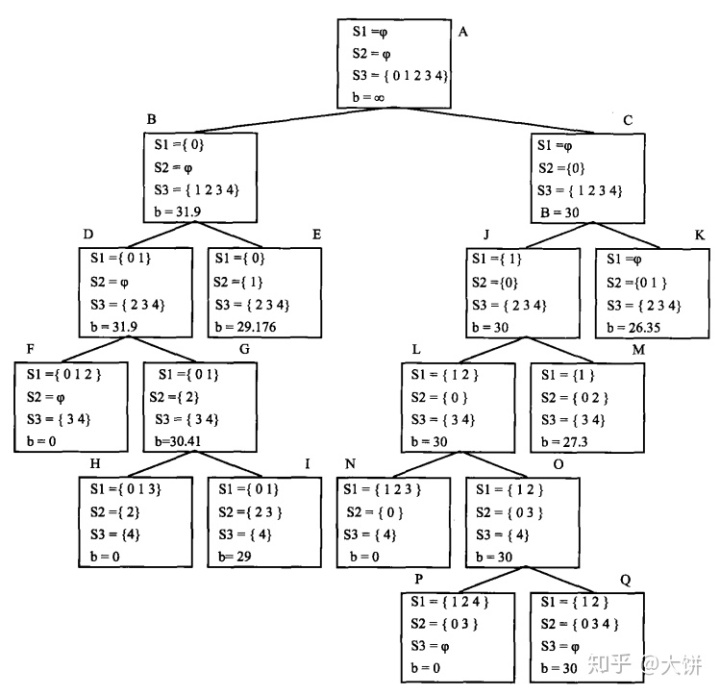
还有更多的示例请参考原文:
分支限界法——对解空间的一种策略搜索(广度优先搜索)www.jianshu.com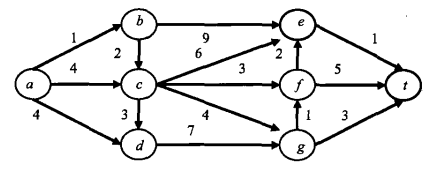



















 7986
7986











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








