# 异运算_异分母分数相加，为何要通分？这是我看过的最好的解释

做了几套小升初的数学试卷，发现异分母分数比大小是必考题型。分数是小学阶段孩子最难掌握的知识之一。究其原因，无怪乎是孩子对分数的概念理解不透彻。该怎么协助孩子透彻理解分数呢？

在《儿童怎样学习数学》里，帕梅拉·利贝克说，要理解分数，有两个主要障碍：

分数不能看作是孤立的、单独存在的东西，它只有跟有关的整体联系起来才有意义。

要认识某个东西的几分之几，就需要对这个东西的整体有一个概念。

要想象一个整个苹果，其中你得到四分之一，相对来说，比较容易。但是，要想象一千克的“整体”，其中你得到四分之一；或者是，一小时的“整体”，其中已过去了四分之一，这就不容易了。

理解分数的第二个障碍，是用数学符号来表示分数的这种复杂的记数法。一个分数，下面的这个数字(分母)和上面的这个数字(分子)起的作用完全不同。

2/3这个分数的分母告诉我们的是这个“整体”已经被分成了三个相等的部分，所以念做“三分”；而分子则告诉我们，要考虑是其中的两部分，所以念做“之二”。

这一套分母、分子记数法，使得同一个分数可以有无数个记数法。例如2/3和4/6 、10/15、14/21等等。都是同一个数，这个概念孩子们要花很长的时间来吸收，理解上还可能有别的障碍。

为了克服第一个障碍，我们应该注意在最早的阶段对于任何一个分数都要经常提到与之有关的这个整体。不要只讲“四分之一”，而要讲“一个苹果的四分之一”，“一米的四分之一”，或者是“十二的四二分之一”等等。

为了克服第二个障碍，我们应该在孩子们较好地形成了概念之前，避免使用分数的记数法。只有1/2这个符号是例外，因为在生活中用的比较广泛。可以让孩子们把它念做“半”。至于这个符号为什么是由“1”和“2”组成，就不要作任何解释。

要协助孩子理解分数这个概念，有一本书值得参考。在安野光雅的《走进奇妙的数学世界》系列的第一册里，安野光雅把比较分数的大小，转化成了比高矮，思路独特又直观。朵爸建议大家找到读一读。

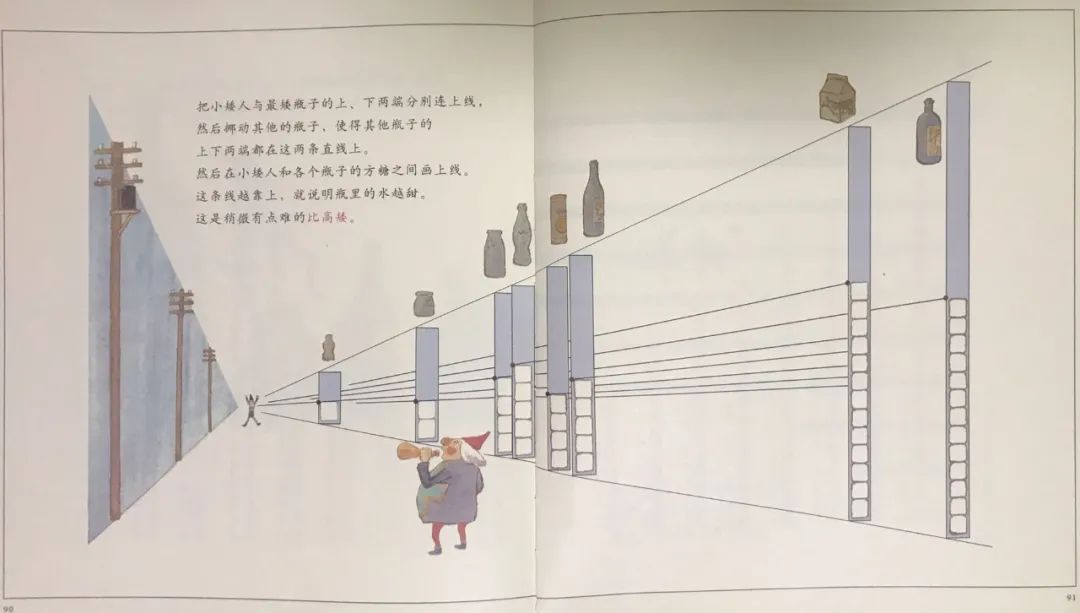
安野光雅举了个例子。拿几个瓶子和不同数量的方糖摆开，问：哪个瓶子里的水最甜呢？

看一下水中有几块方糖就能比较出来。在水量相同的情况下，方糖越多，水就越甜。

如果水量不同，该怎么办呢？此时，如果糖量一定时，水量越少越甜。

把分母比作水，分子当作糖，2/3 vs 1/3，是水量相同，糖多的更甜；5/8 vs 5/6是糖量相同，则水少的更甜。

可是，如果水量和糖量都不同，事情就麻烦了。这相当于分母和分子都不同。

举个例子：

A、5克水中含有1克糖。

B、8克水中含有3克糖。

比较A和B，哪一个的糖分比值高时，会用到分数。A是1/5，B是3/8，通分后A是8/40，B是15/40，然后求其差，B的糖分比值比A多7/40。

用柱状图表示就是图1，让图的高度相同，就与计算时要通分的情形一样，换句话说，就是应用了“水量一定时，糖越多就越甜”这一规律。

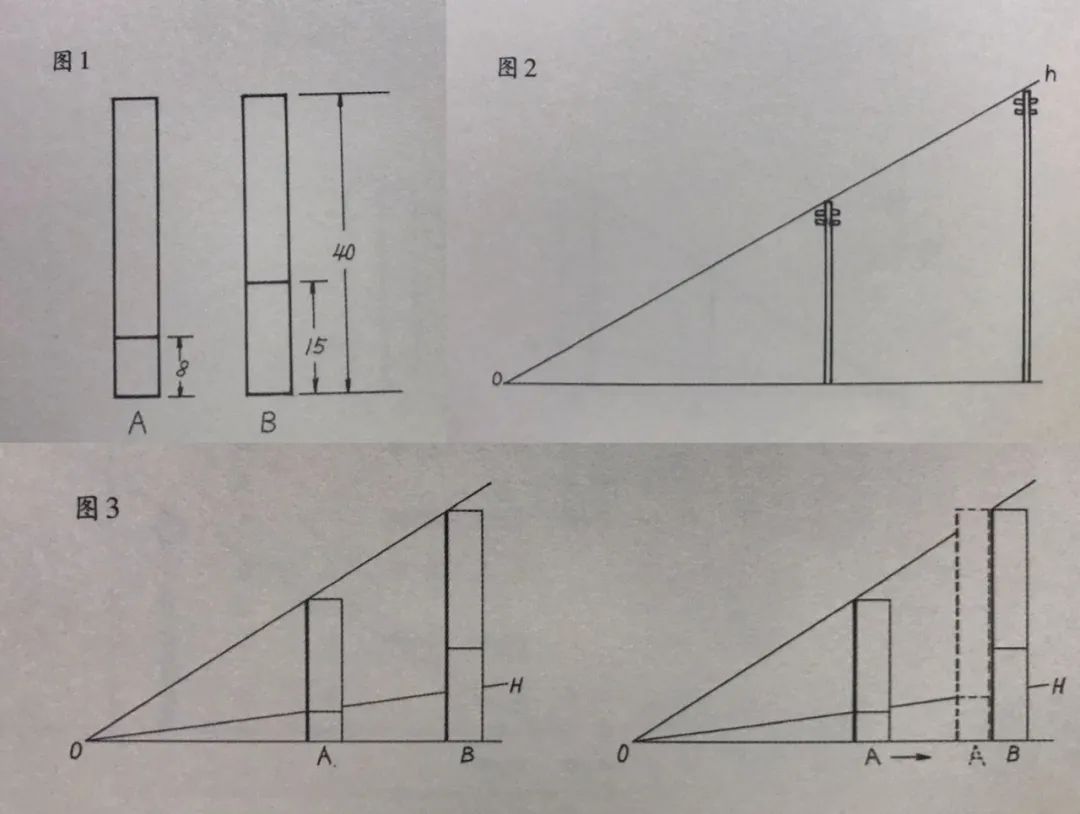
电线杆远看虽小，实际上的高度应该是相同的。这就是绘画中的透视法原理，与几何学中的比例意义相同。如果让电线杆沿着oh线移动，向右时就会扩大，向左时就会缩小。

利用这个方法，可以把水量少和水量多的溶液设定成同样的高度。在这种情况下，虽然溶液高度是相同的，但其中水和糖的比值并没有改变(相当于分子分母同时扩大了相同倍数，但比率不变)。

图3就是这样的应用，连接OH这条线，就是为了让A和B水量相同以后，用糖的高度来做比高矮，从而知道谁更甜。这是数学上典型的转化思维。把浓度比率转化为比较高与矮。

通分的理由只有一个，化成相同的计数单位

异分母分数相加减，先通分，化成相同的计数单位，再相加减。学过的加减法运算，还有哪些？是否也有相同的地方呢？

不管是整数加减法，还是小数加减法，都要对位相加，就是位值要对应，不能百位跟十位加，或者个位跟十分位相加。这是相同计数单位相加减。(顺带还可以复习下之前写过的“数位”知识。“数位”与“位数”是意义不同的概念，注意区分。)

整数、小数、分数的加减法运算，都是把相同的计数单位的个数相加减。这就帮孩子把整个知识串联起来。

可是分数的本质到底是什么？为什么需要分数？下一篇我们再来讲一讲。