一阶rc电路时间常数_“一阶线性电路暂态分析”的“时间表”分析法-CSDN博客

本文链接：https://blog.csdn.net/weixin_40000999/article/details/111710799

对于只含有一个储能元件或可等效为一个储能元件的线性电路，不论电路简单还是复杂，其微分方程都是一阶常系数线性微分方程，这种电路称为一阶线性电路，简称一阶电路。

一阶电路暂态分析是电工学中电路部分的重点内容，也是学习的难点。由于教学内容相对抽象，加之学时有限，教学效果一直差强人意。如何理顺教学逻辑，科学提炼整合教学内容，提高教学效果是每一位从事电工学教学工作的教师应认真思考和努力解决的问题。

本人在分析教学效果不佳原因的基础上，结合自己的教学工作总结并实践了一阶电路暂态分析的“时间表”教学法。实践证明，该方法清晰明了，学生易于接受，占用学时少，学习效果明显提高。

请点击输入图片描述

利用“时间表”分析法，快速准确得到储能元件的等效电路

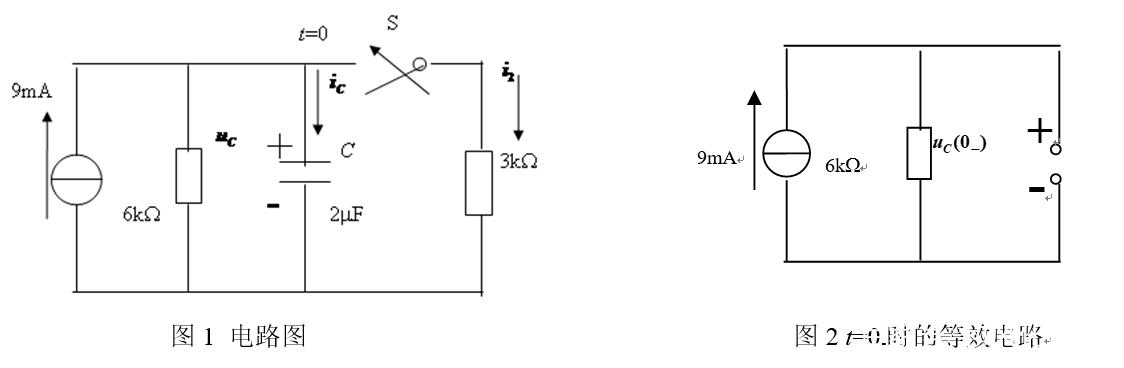
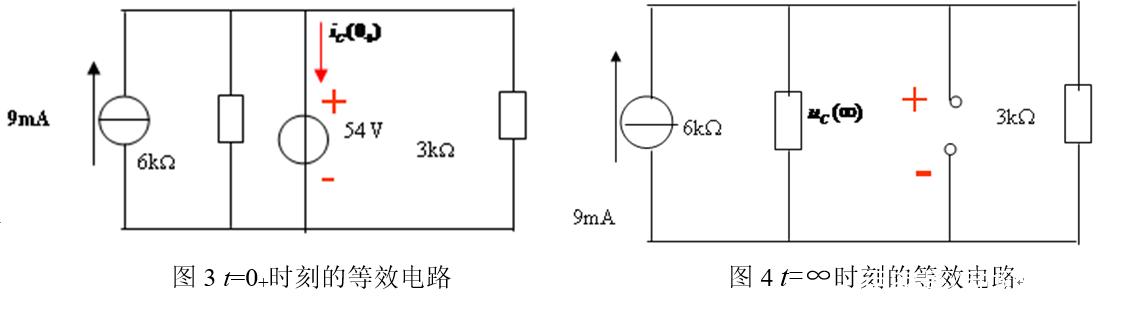
正确求解出初始值、稳态值和时间常数这“三要素”的关键是正确得出储能元件在t=0- ，t=0+和t=∞时刻的等效电路。本人在教学实践中通过时间表分析法帮助学生快速、准确地得到各个时刻的等效电路。

“时间表”分析法的中心思想是根据题意和简单计算罗列出开关S的状态和储能元件在不同时刻的等效电路，让学生按“表”索骥，画出不同时刻的等效电路，原电路被拆分成多个不含有储能元件的电路。对各电路中的电压和电流等的求解转化为前两章电阻电路中所学的内容，学生就很容易得出正确答案了。最后利用“三要素法”得出电路中任何一处的电压和电流的表达式。

例：电路如图1所示，t=0时合上开关S，合S前电路已处于稳态。试求电容电压uc和电流i2和ic。