matlab做三次拉格朗日插值多项式_科学计算第三讲（Hermite插值、龙格现象、分段插值、样条插值）...

第二章、插值理论（续）

上一讲我们介绍了拉格朗日插值法和牛顿插值法，这两者都是对给定

个节点上的函数值来求出

次插值多项式，而现在我们的函数表上又新添加了

个节点上的导数，我们想让插值多项式的性质更加好，因此该多项式不仅要满足于节点上函数值相同，其导数值也要相同，这就是

Hermite插值问题.

※Hermite插值

问题提法：给定函数在

上的函数值

，以及一阶导数值

，要求

次多项式

满足

为啥是

呢？因为这里有

个条件，而

次方程例刚好待定了这么多系数，下面我们具体来求Hermite插值多项式：

可以受拉格朗日插值法的启发，用基函数的思想将所求多项式表示为

其中基函数

都是不超过

次的多项式，且满足

也就是

负责控制函数值，

负责控制一阶导数值.

首先来求

，它满足

也就是说在这

个节点上，它的函数值和导数值都是0，也就是二重零点，所以我们得到它的

个因子

.再由

又能得到它的一个因子

，我们发现这些因子乘起来已经到

次了，所以设

再由最后一个条件

求解待定系数

即可，其化简后可以表示成

其中

就是拉格朗日插值的基函数.

其次我们来确定

，与前面一样，能得到因子

，但由于它在

点的函数值不为0，因此我们不能再获得更多的因子，所以只能待定系数为

然后利用

，通过解二元线性方程组来求得待定系数，

注意这里前面的待定一次多项式也可以设成

，这样计算上会方便一些！

最后化简得到结果

这个公式应该是不需要记忆的，反正考试的时候一般也是两个点的情形，重要的是掌握前面待定的方法.

对于上面所求出的，满足函数值与导数值要求的多项式，有如下误差估计：

证明 还是构造有较多零点的函数，反复利用罗尔定理

在拉格朗日法的误差估计中，我们构造过类似的函数，这里可以借鉴那个形式，构造的函数为

这个函数不仅有

个零点，而且这

个零点还是二重零点。我们先通过

个零点，利用罗尔定理得到

个一阶导数零点，进而加上原来的

个一阶导数零点，一共有

个一阶导数零点，再反复用就能得到

，这也就是误差估计的结论。注意，我们在讲Hermite插值时没有证明它的存在唯一性，但是到此为止我们

通过构造形式可知它的存在性， 通过误差估计式可知它的唯一性（如果有两个，那么将其中一个看成另外一个的Hermite插值多项式）

下面给几个例子，其中有带有技巧性的，也有用上面讲的一般方法的：

例1 已知三点函数值和一点导数值

求不超过3次的插值多项式

满足

法1 题目条件和拉格朗日法的条件相比就多了一个，因此我们想，是不是能利用拉格朗日插值公式，添加一项来得到？

拉格朗日插值公式为

它和所求的多项式之差有3个零点

通过这3个零点就可以得到3个因子，进而待定系数为

再通过

求解待定的系数

即可，求出的形式用字母表示比较复杂，但这个方法还是很容易理解和掌握的.

法2 也就是上面讲的基函数法

设

其中这些待求函数都是不超过3次的多项式，且满足

逐个写出能得到的因子，并待定系数如下

通过剩余的条件求解待定的系数即可，思路比较常规.

例2

，求三次插值多项

式满足

解 根据线性性质，我们只要求

的满足类似条件的插值多项式

即可.

这里我们不能得到任何因子，但注意到三次多项式的二阶导数是一次多项式，因此我们可以先求出二阶导数，它可以用两点式求出，结果为

通过不定积分能够得到

再利用

就能得到待定的系数，这样比直接待定三次多项式求四个系数来的简便，但关键是能否想到先求二阶导数.

例3 设

，求4次多项式

满足

解 第一次遇到会很难想到最简单的思路，实际上这里给了比较多的导数信息，可以利用泰勒展开式待定系数如下：

再利用

得到

即可.

例4 设

是一个

次多项式，满足

求

如果没有做过，还是很难想到，不过既然在老师的课件上就还是放上来吧，谁知道会不会考到呢。

解 令

，则它是一个

次的多项式，且由很多个零点

进而可以待定为

最后注意到

，可以求出

，然后再求

即可.

---

在学习完拉格朗日插值后，我们很自然地会想：是不是使用更多的节点，将插值多项式的次数弄的更高，这样近似的效果更好？而实际上并不是，考察下面这个例子

例

定义在区间

上，利用等距节点构造插值多项式，则

是无界的，其中

的情形如下图所示

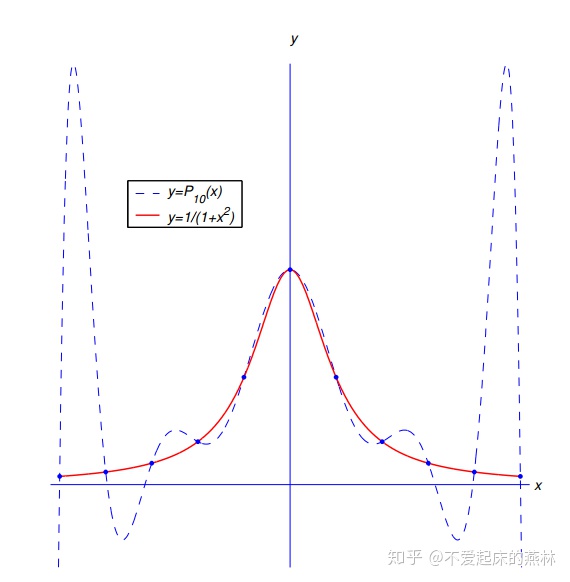
可以看出，在区间的端点附近，插值多项式发生剧烈的振荡，这是如果我们再用插值多项式的值来近似函数值的话，会有非常大的误差，这就是Runge现象.

不知道大家还记不记得数学分析中学过的魏尔斯特拉斯定理，它说的是任何一个函数都能用一个次数足够高的多项式进行逼近，这是不是和Runge现象矛盾了呢？实际上并没有，因为魏尔斯特拉斯定理中并没有要求多项式的值在给定点上与函数值相同，事实上我们有下面两个定理结果：

Faber定理：通过任意规则给定插值节点

则存在一个连续函数，它在这组节点上插值多项式不收敛与它.

插值收敛性定理：给定连续函数，则存在某种规则下得到的一组插值节点

使得这个函数在这组插值节点上的插值多项式收敛于它.

其中Faber定理告诉我们，使用一种特定的规则（如取等距节点），盲目地增加插值多项式的次数是不合理的；而插值收敛性定理虽然保证对于任何连续函数都有一组插值节点能很好地收敛，但也没有给出求节点的方法。为了保证插值多项式在区间划分足够精细后，能够收敛于目标函数，我们引进了分段插值.

※分段插值

• 分段线性：顾名思义，就是将区间分成很多个小区间，然后每个小区间上用线性插值多项式.

分段线性插值

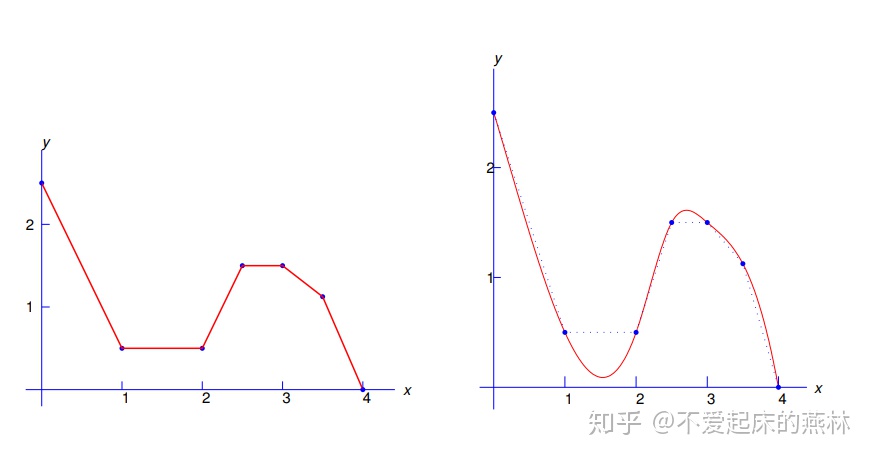
由上一讲的一道例题（忘了可以翻下），在每个小区间上有误差估计：

其中

.然后我们将区间扩大为整个定义域得到

其中

• 分段k次插值：顾名思义，就是将节点进行组合，每
  个为一组，在这组节点上构造
  次插值多项式

分段k次插值

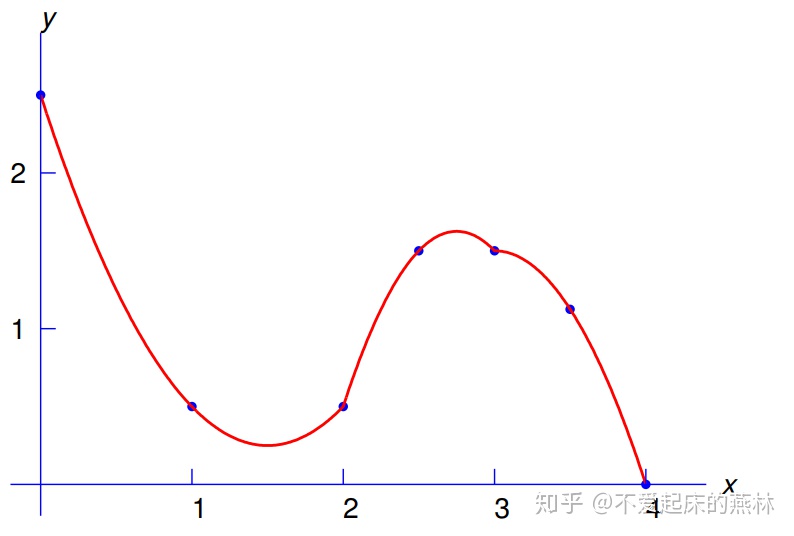
• 分段3次Hermite插值：顾名思义，将整个区间划分为
  个小区间，在每个小区间上用两个端点的函数值和导数值构建三次Hermite插值多项式。这里需要注意，利用分段3次Hermite插值得到的插值函数，由于在相邻区间的公共点处导数值相同，因此该插值函数的
  一阶导数是连续的.

其误差余项为

这里

得到这个结果需要利用每个小区间上的Hermite插值余项

再结合基本不等式

即得.

分段Hermite插值性质已经比较好了，但是下面这个方法能够得到收敛且二阶导数连续的插值多项式：

※样条插值

问题提出：设在区间

上给定函数值

现要求构造样条插值函数

满足下面三个条件:

在每个小区间

上是不超过3次的多项式、

注意，这三个条件不能确定

,因为一共有

个区间，每个区间上为3次多项式，共有

个待定系数。由

中每个区间两个端点的函数值条件能写出

个方程，由

，在非端点的

个点上，相邻两个多项式的一阶导数和二阶导数值相同，这样有

个方程，因此还少两个条件。

一般来说可以补充下面三类条件：

曲线在两个端点

处一阶导数已知

曲线在两个端点

处二阶导数已知，称为自然样条

周期条件。即