一道简单的几何题

• 求解下图中阴影部分的面积，假设正方形的边长为1

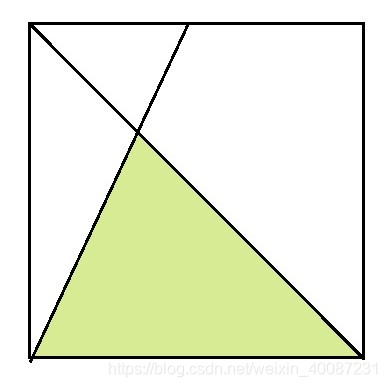
画辅助线：为对顶的两个三角形作高线

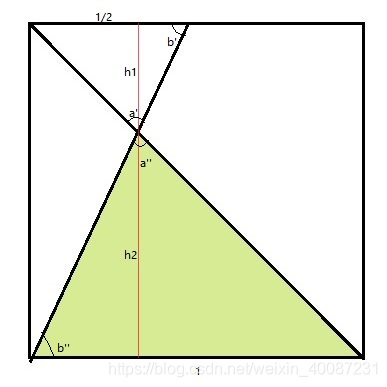
  第一步：定理 ：两角分别对应相等的两个三角形相似。 关注对顶的两个三角形
  证  明：1.平行线的相交线内角相等，2.两个顶角相等， 因此这两个三角形有两个角相等，则为相似三角形；
 
  第二步：性质：相似三角形任意对应线段的比等于相似比。
  求相似比：对顶的两个三角形，其中两个底边分别在正方形边上，为对应边。因此相似比(上比下) r = 1/2;
 
  第三步：性质：相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比
  求高线：由于两个三角形的高之和等于1；且两者高之比为1:2；因此底部三角形的高占比为2/3；因此 h = 1* 2/3;
 
  第四步：性质：三角形面积 = 1/2*底边长*高。
  求面积：底部三角形面积为：S=1/2 * 1 * 2/3 = 1/3 ,因此整个阴影部分面积为正方形面积的三分之一；

终极思考：图中每一块的面积是多少呢？

先给出答案，具体思路大家自行思考：