数据结构与算法分析~笔记7图（2）

最小生成树是图的一种特殊应用，这个概念可以应用到许多实际问题中去解决关于最小代价的问题。

7.4 最小生成树

连通图的每一棵生成树，都是原图的极小连通子图，也就是原图的一个极大无环子图，它包含原图中的所有顶点，而且有尽可能少的边。这意味着对于生成树来说，若删除它的一条边，就会使该生成树变成非连通图；若给它增加一条边，就会形成图中的一个回路。条边，就会形成图中的一个回路。按照不同的遍历算法，得到的生成树不同；从不同的顶点出发，得到的生成树也有所不同。对于一个连通带权图而言，生成树不同，每棵树的权值（即树中所有边上的权值总和）也可能不同。
设G(V,E)是一个无向连通网，其生成树上任一条边的权值称为该边的代价（Cost），一棵生成树的代价就是树上各边代价之和。在G的所有生成树中，代价最小的生成树称为最小代价生成树（Minimum Cost Spanning Tree），简称最小生成树。
按照生成树的定义，若连通带权图由n个顶点组成，则其生成树必含n个顶点，n-1条边。因此，构造最小代价生成树的准则有3条：
（1）只能使用该网络中的边来构造最小生成树；
（2）能且只能使用n-1条边来连接网络中的n个顶点；
（3）选用的n-1条边不能产生回路。
构造最小生成树的方法较多，多数利用了最小生成树的一种性质，简称为MST：假设N(V,{E})是一个连通网，U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值（代价）的边，其中u∈U,v∈V-U，则必存在一棵包含边(u,v)的最小生成树。
构造最小生成树的典型算法的有两种：Kruskal算法和Prim算法。这两个算法都利用了MST性质，采用逐步求解的策略，亦称贪心策略：给定带权图N={V,E}，V中共有n个顶点。首先构造一个包括全部n个顶点和0条边的森林F={T0,T1,LTn-1}，然后不断迭代。每经过一轮迭代，就会在F中引入一条边。经过n-1轮迭代，最终得到一棵包含n-1条边的最小生成树。
需要指出的是，同一带权图可能有多棵最小生成树，但所有不同的最小生成树的代价是相同的。

Kruskal算法的基本思想：设一个有n个顶点的连通网络N={V,E}。首先构造一个由这n个顶点组成，不含任何边的图T={V,ϕ}，其中每个顶点自成一个连通分量。不断从E中取出代价最小的一条边（若有多条，任取其一），若该边的两个顶点来自T中不同的连通分量，则将此边加入到T中，否则舍去此边选择下一条代价最小的边。依此类推，直到T中所有的顶点在同一个连通分量上为止。下图所示为依照Kruskal算法构造一棵最小生成树的过程。

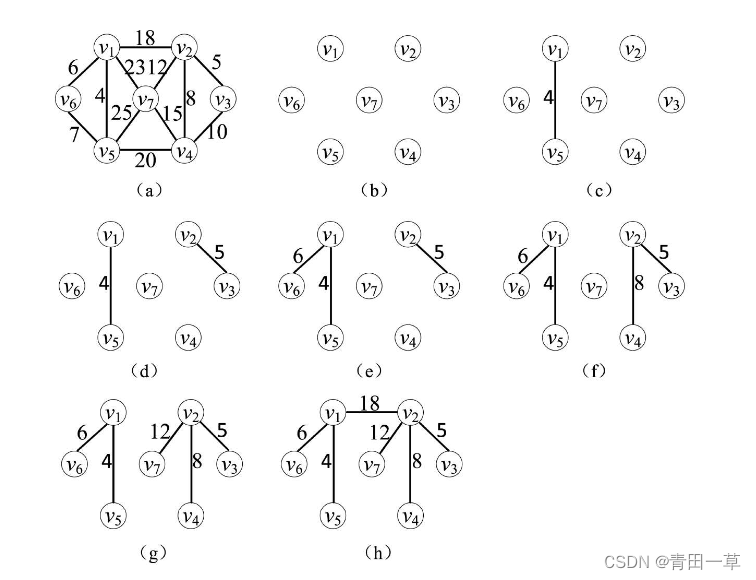
在上述构造过程中，代价分别为4,5,6的3条边由于满足条件先后被加入到集合T中，代价为7的边被舍去，因为它依附的两个顶点在同一连通分量上，它若加入T中，会使T中产生回路。然后代价为8的边加入集合T。同理，代价为10的边被舍弃，然后代价为12的边加入集合T，最后一条代价为18的最小的边将两个连通分量连接起来且不形成回路，则代价为18的边可加入集合T中。由此，用Kruskal算法构造出一棵最小生成树。
Kruskal算法的时间复杂度为O(loge)，其中，e为无向连通网络中边的数目。因此，Kruskal算法适合于求边稀疏的网的最小生成树。

Prim算法也是不断迭代进行的，其基本思想：给定任意一带权连通网络N={V,E}，T=(U,TE)是G的最小生成树。算法始终将顶点集合V分成没有元素重叠的两部分,V=U∪(V-U)，T的初始状态为U={u0}(u0∈V),TE=ϕ，然后重复执行以下操作：在所有u∈U,v∈V-U的边（中找出一条代价最小的边(u0,v0)并入集合TE，同时v0并入U，直至U=V为止。此时TE中必有n-1条边，则T就是G的最小生成树。
为实现这个算法，需附设一个辅助数组closedge，以记录从U到V-U具有最小代价的边。对每个顶点vi∈V-U，在辅助数组中存在一个相应分量closedge[i-1]，它包括两个域，其中，lowcost域存储该边的权值。显然，

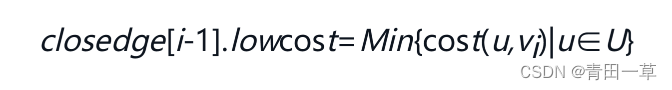
vex域存储该边依附的在U中的顶点。下图所示为依照Prim算法构造无向连通网的一棵最小生成树的过程，在构造最小生成树的过程中辅助数组中各分量值的变化如下表所示。


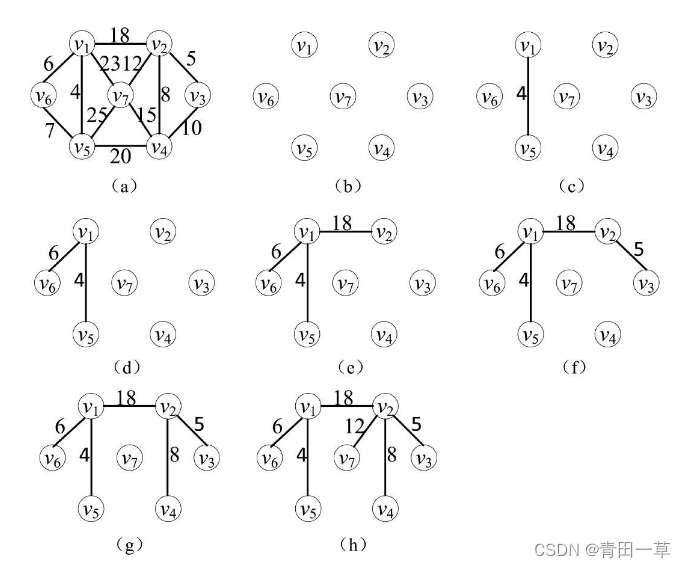
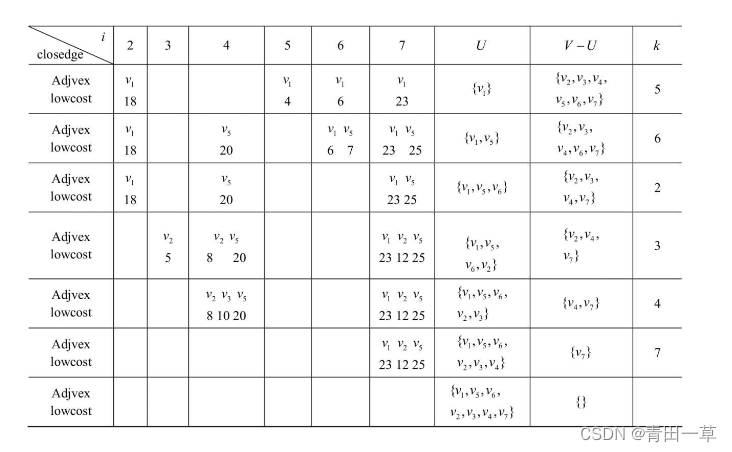
Prim算法的时间复杂度为O(n2)，与网中的边数无关，只与顶点数n相关。因此Prim算法与Kruskal算法刚好相反，它适用于求边稠密的网的最小生成树。

7.5 有向无环图及其应用

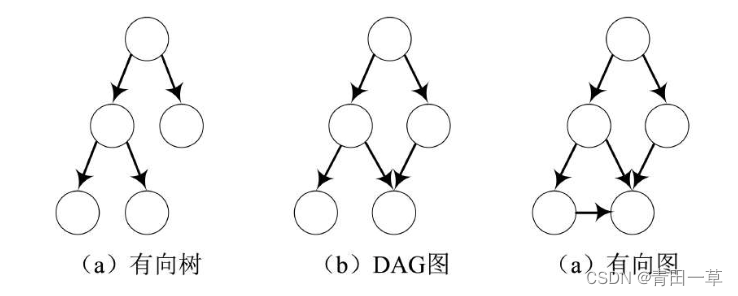
一个无环的有向图称为有向无环图（Directed Acycline Graph），简称DAG图。图中分别列举了有向树、DAG图和有向图的例子。

有向无环图是描述含有公共子式的表达式的有效工具。例如下述表达式：

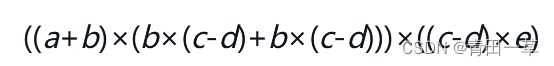
它可以利用二叉树来表示，如图（a）所示。仔细观察该表达式，可以发现一些相同的子表达式，如(c-d)和b×(c-d)等。在二叉树中，表示这些子表达式的子树也重复出现。若利用有向无环图，则可实现对相同子式的共享，从而节省存储空间。例如图（b）所示为表示同一表达式的有向无环图。

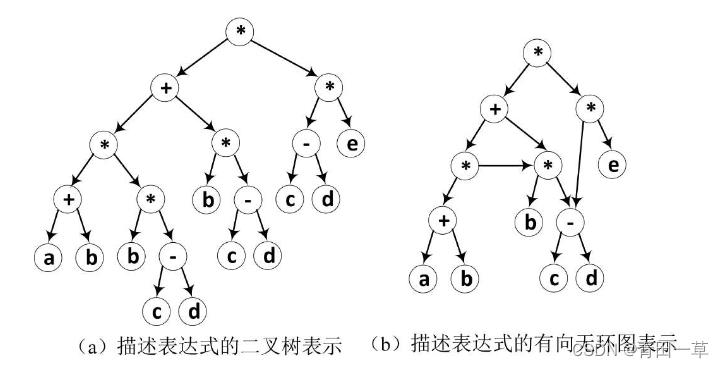
检查一个有向图是否存在环要比无向图复杂。对于无向图来说，若深度优先遍历过程中遇到回边（即指向已访问过的顶点的边），则必定存在环；而对于有向图来说，这条回边有可能是指向深度优先生成森林中另一棵生成树上顶点的弧。
有向无环图也是描述一项工程或系统的有效工具。大部分工程项目都可以分为若干个活动的子工程，而这些子工程之间，通常受着一定条件的约束，如某些子工程的开始必须在另一些子工程完成之后。对于整个工程和系统，人们一般普遍关心两个问题：一是工程能否顺利进行；二是估算整个工程完成所必须的最短时间。

所有的工程或者某种流程可以分成若干个小的工程或阶段，这些小的工程或阶段就称为活动（Activity）。若以图中的顶点来表示活动，有向边表示活动之间的优先关系，则这样活动在顶点上的有向图称为AOV网（Activity On Vertex Network）。在AOV网中，若从顶点i到顶点j之间存在一条有向路径，称顶点i是顶点j的前驱，或者顶点j是顶点i的后继。
拓扑排序（Topological Sort）就是由某个集合上的一个偏序得到该集合上的一个全序的操作。
若集合X上的关系R满足自反、反对称和传递性，则称R是集合X上的偏序（Partial Order）关系。设R是集合X上的偏序，如果对每个x,y∈X必有xRy或yRx，则称R是集合X上的全序关系。
一个表示偏序的有向图可用来表示一个流程图。它或者是一个施工流程图，或者是一个产品生产流程图，再或者是一个数据流图（每个顶点表示一个过程）。图中每一条有向边表示两个子工程之间的次序关系。
在AOV网中，不应该出现有向环，因为存在环意味着某项活动应以自己为先决条件。
对给定的AOV网应首先判断网中是否存在环。检测的办法是构造有向图顶点的拓扑有序序列。若网中所有的顶点都在它的拓扑有序序列中，则该AOV网中必定不存在环。
构造有向图顶点的拓扑排序的步骤如下：
（1）在有向图中选一个没有前驱的顶点，输出之。
（2）从图中删除该顶点以及从该点出发的全部有向边。
（3）重复上述两步，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点。
拓扑排序操作的结果可能有两种：
（1）网中全部顶点都被输出，这说明网中不存在有向回路；
（2）网中顶点未被全部输出，剩余的顶点均有前驱顶点，这说明网中不存在回路。
下图（a）中的有向图为例，图中v1和v2没有前驱，从中任选一个进行输出。假设先输出v1，在删除v1及弧<v1,v3>，<v1,v4>之后，v2和v3均无前驱，任选v3进行输出且删去v3及弧<v3,v6>，<v3,v7>，之后v2和v6无前驱，依此类推，可从中任选一个进行下去。整个拓扑排序的过程如图7.28所示。最后得到该有向图的拓扑有序序列为：v1→v3→v6→v2→v4→v5→v7。

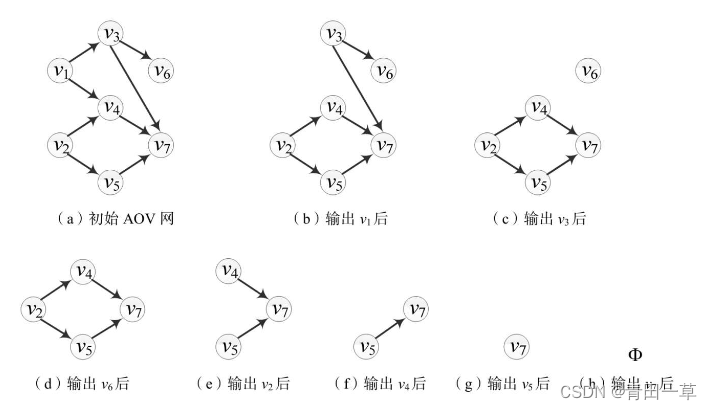
如何在计算机中实现拓扑排序呢？针对上述两步操作，可以采用邻接表作为有向图的存储结构，并在头结点中增加一个存放顶点入度的数组。入度为零的顶点即为没有前驱的顶点；删除顶点及从它出发的全部有向边的操作，可用弧头顶点入度减1的方式来实现。
AOE网（Activity On Edge Network），即边表示活动的网。AOE网是一个带权的有向无环图。其中，顶点表示事件（Event），弧表示活动，权表示活动持续的时间。通常，AOE网可以用来表示工程的进度计划。
下图所示是一个有11项活动（即11条边）的AOE网。其中，有9个事件v1,v2,v3,…,v9，每个事件表示在它之前的活动已经完成，在它之后的活动可以开始。如v1表示整个工程开始，v9表示整个工程结束，v5表示a4和a5已经完成，a7和a8可以开始。与每个活动相关的数字是执行该活动所需的时间。比如，完成活动a1需要6天，a2需要4天。

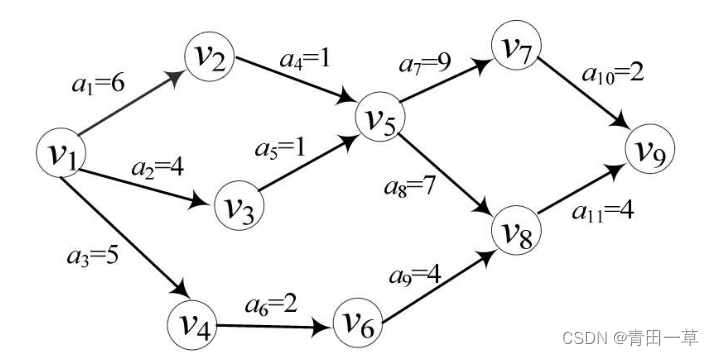
由于整个工程只有一个开始点和一个完成点，故在正常情况（无环）下，网中只有一个入度为零的点，称之为源点（Source）；一个出度为零的点，称之为汇点（Sink）。
在AOE网络中，有些活动可以并行地进行。从源点到各个顶点，以及从源点到汇点的有向路径都可能不止一条，这些路径的长度可能不同，完成不同路径所需的时间也可能不同，但只有各条路径上所有的活动都完成了，整个工程才算完成。因此，完成整个工程所需的时间取决于从源点到汇点的最长路径的长度，即在这条路径上所有活动的持续时间之和，这条最长的路径就叫做关键路径（Critical Path）。
要找出关键路径，必须找出关键活动（Critical Activity），即不按期完成就会影响整个工程完成的活动。关键路径上所有的活动都是关键活动。
下面定义几个与计算关键活动相关的量。
（1）假设开始点是v1，从v1到vi的最长路径长度叫做事件vi的最早开始时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。用e(i)表示活动ai的最早开始时间。
（2）一个活动的最迟开始时间l(i)，定义为在不推迟整个工程完成的前提下，活动ai必须最迟开始的时间。
（3）两者之差l(i)-e(i)意味着完成活动ai的时间余量。把l(i)-e(i)=0的活动叫做关键活动。显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快整个工程的进度。
因此，分析关键路径的目的就是辨析哪些是关键活动，以便争取提高关键活动的功效，缩短整个工期。
由以上分析可知，辨析关键活动就是要找出l(i)=e(i)的活动。为了求得AOE网中活动的l(i)和e(i)，首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧<j,k>表示，其持续的时间记为dut(<j,k>)，则有如下关系：

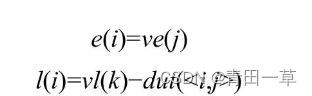
求ve(j)和vl(j)需分两步进行：① 从ve(0)=0开始向前递推：

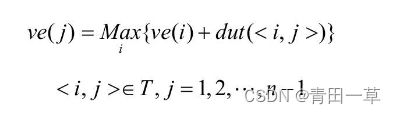
其中，T是所有以第j个顶点为头的弧的集合。
② 从vl(n-1)=ve(n-1)起向后递推：

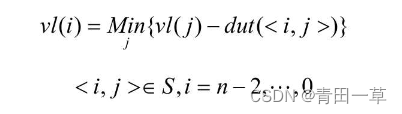
其中，S是所有以第i个顶点为尾的弧的集合。
这两个递推公式的计算必须分别在拓扑有序和逆拓扑有序的前提下进行。也就是说，ve(j-1)必须在vj的所有前驱的最早发生时间求得之后才能确定，而vl(j-1)则必须在vj的所有后继的最迟发生时间求得之后才能确定。因此，可以在拓扑排序的基础上计算ve(j-1)和vl(j-1)。
由此得到如下求关键路径的算法。
（1）输入e条弧<j,k>，建立AOE网的存储结构。
（2）从源点v0出发，令ve[0]=0，按拓扑有序求其余各顶点的最早发生时间vei。如果得到的拓扑有序序列中顶点个数小于网中顶点数n，则说明网中存在环，不能求关键路径，算法终止；否则执行步骤（3）。
（3）从汇点vn出发，令vl(n-1)=ve(n-1)，按逆拓扑有序求其余各顶点的最迟发生时间vli；
（4）根据各顶点的ve和vl值，求每条弧s的最早开始时间e(s)和最迟开始时间l(s)。若某条弧满足条件e(s)=l(s)，则为关键活动。
如上所述，计算各顶点的ve值是在拓扑排序的过程中进行的，需对拓扑排序的算法做如下修改：
① 在拓扑排序之前设初值，令ve[i]=0(0≤i≤n-1)；
② 在算法中增加一个计算vj的直接后继vk的最早发生时间的操作：若ve[j]+dut(<j,k>)>ve[k]，则ve[k]=ve[j]+dut(<j,k>)；
③ 为了能按照逆拓扑有序序列的顺序计算各顶点的vl值，需记下在拓扑排序的过程中求得的拓扑有序序列。这需要在拓扑排序算法中增设一个栈以记录拓扑有序序列，则在计算求得各顶点的ve值之后，从栈顶至栈底便为逆拓扑有序序列。
下面则是改写之后的算法和求关键路径的算法。
由于逆拓扑排序必定在网中无环的前提下进行，则亦可利用DFS函数，在退出DFS函数之前计算顶点v的vl值（因为此时的v的所有直接后继的vl值都已求出）。
这两种算法的时间复杂度均为O(n+e)，显然，前一种算法的常数因子要小些。由于计算弧的活动最早开始时间和最迟开始时间的复杂度为O(e)，所以总的求关键路径的时间复杂度为O(n+e)。
由于网中各项活动是互相关联的，影响关键活动的因素也是多方面的，任何一项活动持续时间的改变都会影响关键路径的改变。而且，只有在不改变关键路径的情况下，提高关键活动的速度才是有效的。另一方面，若网中有几条关键路径，那么，单是提高一条关键路径上的关键活动的速度，还不能导致整个工程缩短工期，必须要提高同时在几条关键路径上的活动的速度。

7.6 最短路径

而在一个不带权的图中，若从一个顶点到另一个顶点存在着一条路径（仅限于无回路的简单路径），则称该路径的长度为该路径上经过的边的数目，它等于该路径上的顶点数减1。
由于从一个顶点到另一个顶点可能存在着多条路径，每条路径上所经过的边数可能不同，即路径长度不同，则称路径长度最短（经过的边数最少）的那条路径为最短路径，其路径长度叫做最短路径长度或最短路径。
若图是带权图，则把从一个顶点到图中其余任一个顶点的一条路径上所经过边上的权值之和定义为该路径的带权图路径长度，由于可能不止一条路径，因此把带权图路径长度最短（权值最小）的那条路径也称作最短路径，其权值之和也称作最短路径长度或最短路径。
求图的最短路径问题包括两个方面：
（1）求图中一个顶点到其余各顶点的最短路径；
（2）求图中每对顶点之间的最短路径。
单源最短路径
首先利用Dijkstra算法解决单源最短路径问题：给定带权有向图G和源点v，求从v到G中其余各点的最短路径。
下图所示带权有向图G中从顶点v1到图中其余各个顶点之间的最短路径所示。如下表所示：


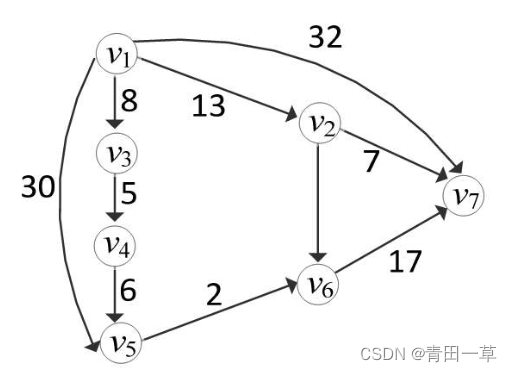
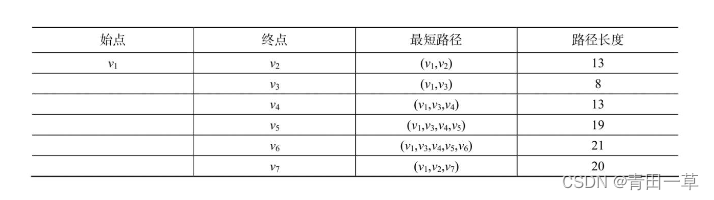
求图中一个顶点到其余各顶点的最短路径，常用Dijkstra算法。该算法设置一个集合S，记录已求得最短路径的顶点，初始时把源点u0放入S中。此外，在构造过程中还设置了两个辅助数组：
dist[]：存放集合S内顶点到S外各顶点的边上的当前最小权值；
path[]：记录集合S外各顶点距离集合S内哪个顶点最近（权值最小）。
假设选择从顶点0出发，即u0=0，因为在集合S内最初只有一个顶点0，故在path数组中，只有表示顶点0的数组path[0]=-1，其他都是0，表示集合S外各顶点(）距离集合S内最近的顶点是0。数组dist[i]的内容都是从邻接矩阵的第0行复制来的。然后反复做以下工作。
（1）在dist[]中选择path[i]≠-1且dist[i]最小的边i，用v标记它，则选中的权值最小的边为(path[v],v)，相应的权值为dist[v]。
（2）将path[v]改为-1，表示它已加入集合S。将边(path[v],v,dist[v])加入生成树的边集合。
（3）取dist[i]=min{dist[i],Edge[v][i]}，即用集合S外各顶点i到刚加入该集合的顶点v的距离Edge[v][i]与原来i到集合S中顶点的最短路径dist[i]做比较，取距离近的作为这些集合外顶点到集合S内顶点的最短路径。
4）如果从集合S外顶点i到刚加入该集合的顶点v的距离比原来它到集合S中顶点的最短路径还要近，则修改nearestx[i]=v，表示集合S外顶点i到S内顶点v当前距离最近。

只采用Dijkstra算法求解源点到某一个特定终点的最短路径，其时间复杂度也仍是O(n2)。
每对顶点间的最短路径
可以采用Dijkstra算法求解每对顶点间的最短路径：即每次以一个顶点为源点，重复执行Dijkstra算法n次，其时间复杂度为O(n3)。
Floyd提出的另一个算法，即求各个顶点之间最短路径的Floyd算法，其时间复杂度也是O(n3)，形式上更简单些。
Floyd算法仍是从图的带权邻接矩阵cost出发，其基本思想是：假设求从顶点vi到顶点vj的最短路径。如果从vi到vj有弧，则从vi到vj存在一条长度为edge[i][j]的路径，该路径不一定是最短路径，尚需进行n次试探。首先考虑路径(vi,v0,vj)是否存在（即判别弧(vi,v0)和(v0,vj)是否存在）。如果存在，则比较(vi,vj)和(vi,v0,vj)的路径长度，取长度较短者为从vi到vj的中间顶点的序号不大于0的最短路径。假如在路径上再增加一个顶点v1，也就是说，如果(vi,…,v1)和(v1,…,vj)分别是当前找到的中间顶点的序号不大于0的最短路径，那么(vi,…,v1,…,vj)就有可能是从vi到vj的中间顶点的序号不大于1的最短路径。将它和已经得到的从vi到vj中间顶点序号不大于0的最短路径相比较，从中选出中间顶点的序号不大于1的最短路径之后，再增加一个顶点v2，继续进行试探。
以此类推。在一般情况下，若(vi,…,vk)和(vk,…,vj)分别是从vi到vk和从vk到vj的中间顶点的序号不大于k-1的最短路径，则将(vi,…,vk,…,vj)和已经得到的从vi到vj且中间顶点序号不大于k-1的最短路径相比较，其长度较短者便是从vi到vj的中间顶点的序号不大于k的最短路径。这样，在经过n次比较之后，最后得到的必是从vi到vj的最短路径。
按照此方法，可以同时求得各对顶点间的最短路径。现定义一个n阶方阵序列：

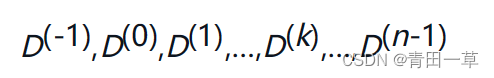
其中：

从上述公式可见，D(1)[i][j]是从vi到vj的中间顶点的序号不大于1的最短路径的长度；D(k)[i][j]是从vi到vj的中间顶点序号不大于k的最短路径的长度；D(n-1)[i][j]就是从vi到vj的最短路径的长度。
关于最短路径的要点：
（1）以上求解最短路径的算法不仅适用于带权有向图，对带权无向图也使用。因为带权无向图可以看作是有往返二重边的有向图，只要在顶点与之间存在无向边，就可以看成是在这两个顶点之间存在两条权值相同、方向相反的的有向边。
（2）解决所有顶点之间的最短路径问题的另一个办法：轮流以每一个顶点为源点，重复执行Dijkstra算法n次，就可求得每一对顶点之间的最短路径及最短路径长度。算法的时间复杂度仍然是O(n3)。