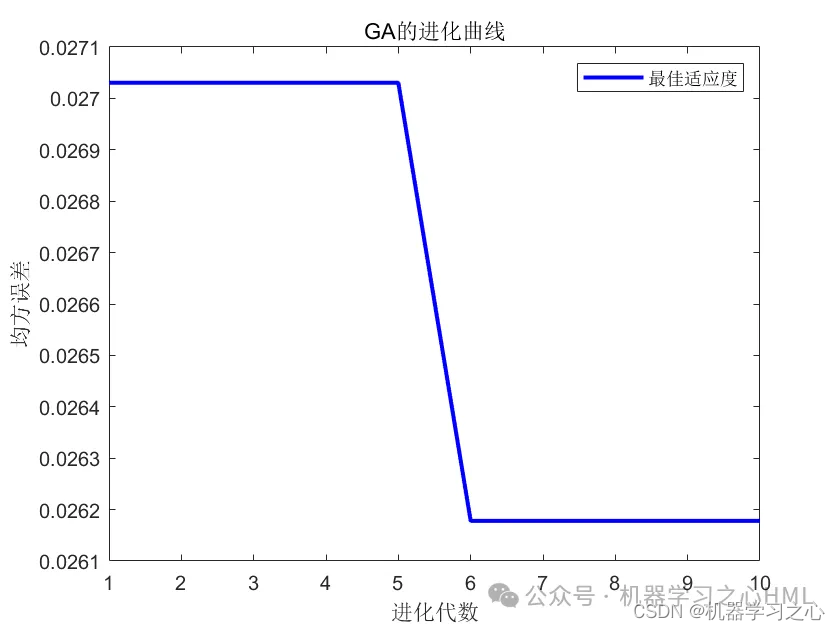
%% 遗传算法优化TCN-LSTM-Attention,实现多变量输入单步预测
clc;
clear
close all
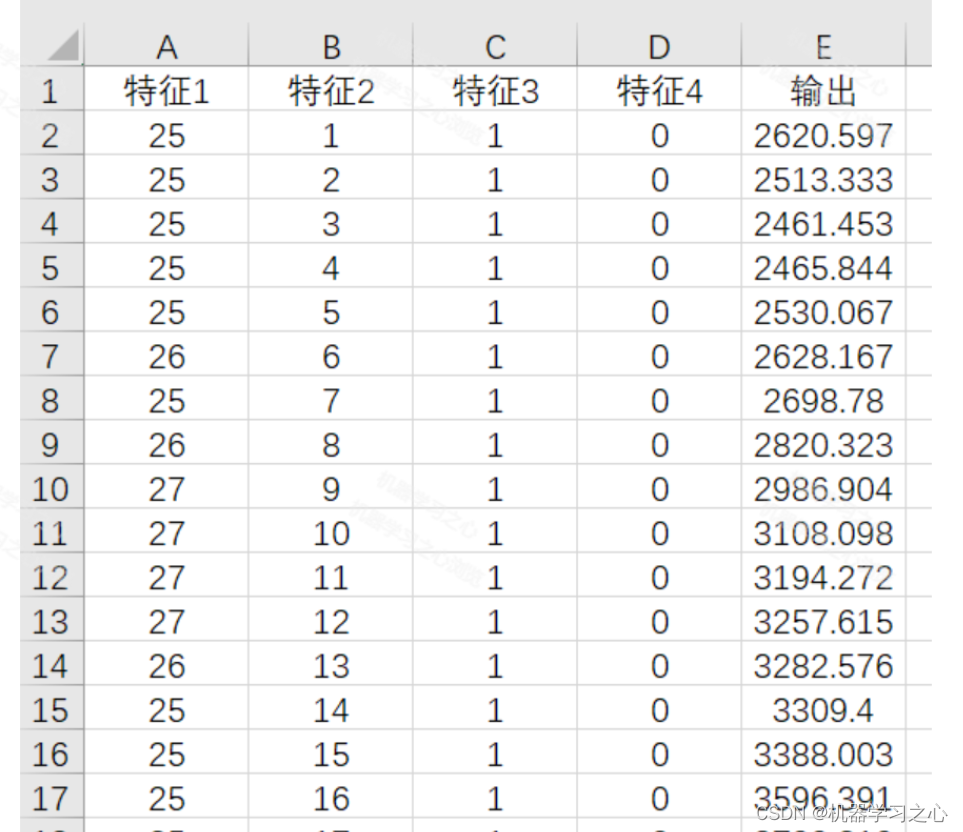
X = xlsread('data.xlsx');
num_samples = length(X); % 样本个数
kim = 6; % 延时步长(kim个历史数据作为自变量)
zim = 1; % 跨zim个时间点进行预测
or_dim = size(X,2);
% 重构数据集
for i = 1: num_samples - kim - zim + 1
res(i, :) = [reshape(X(i: i + kim - 1,:), 1, kim*or_dim), X(i + kim + zim - 1,:)];
end
% 训练集和测试集划分
outdim = 1; % 最后一列为输出
num_size = 0.9; % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
% 格式转换
for i = 1 : M
vp_train{i, 1} = p_train(:, i);
vt_train{i, 1} = t_train(:, i);
end
for i = 1 : N
vp_test{i, 1} = p_test(:, i);
vt_test{i, 1} = t_test(:, i);
end
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








