Java常见排序算法详解

前言

排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

在Java中，排序算法是一种对数据集合中的元素按照特定顺序进行排列的算法。排序算法通常用于将数据按照升序或者降序排列，以便于后续的查找、插入、删除等操作。排序算法在Java中是非常常见和重要的，因为数据的排序是计算机科学中的基本问题之一，几乎所有的应用场景都需要对数据进行排序。

在Java中，排序算法可以针对不同的数据结构实现，例如针对数组、链表、树等。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等。每种排序算法都有其特定的实现方式、时间复杂度和空间复杂度，不同的算法在不同的场景下有着各自的优劣势。

Java提供了丰富的API和工具类来支持排序操作。比如，可以使用 java.util.Arrays 类的 sort() 方法对数组进行排序，该方法内部使用了优化的快速排序算法或归并排序算法；另外，Java中的集合类如 ArrayList、LinkedList 等也提供了 Collections.sort() 方法来对集合进行排序，同样利用了内部的排序算法来实现。

以下是Java中常见的排序算法的介绍：

1. 插入排序（Insertion Sort）

介绍：

插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

工作原理：

• 从第一个元素开始，该元素可以认为已经被排序；

• 取出下一个元素，在已经排序的元素序列中从后向前扫描；

• 如果该元素（已排序）大于新元素，将该元素移到下一位置；

• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；

• 将新元素插入到该位置后；

• 重复步骤2~5。

优点：

• 实现简单直观；

• 对于数据量不大或者部分有序的数据效率较高。

2. 希尔排序（Shell Sort）

介绍：

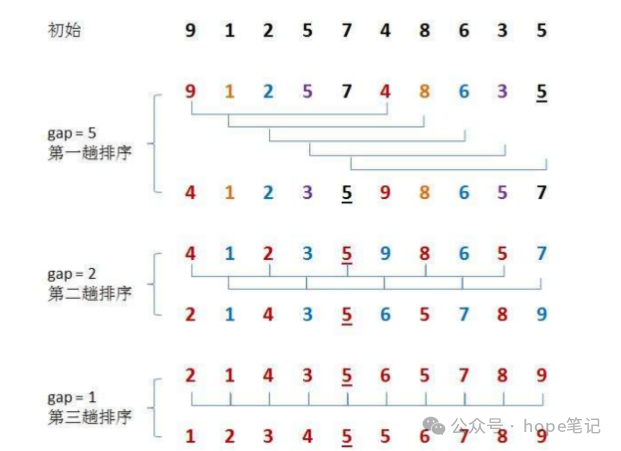
希尔排序是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。

工作原理：

• 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；

• 按增量序列个数k，对序列进行k 趟排序；

• 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。

优点：

• 相比插入排序，希尔排序的数据交换移动次数较少，时间效率有所提升；

• 在数据量较大时，效率高于插入排序。

3. 选择排序（Selection Sort）

介绍：

选择排序是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

工作原理：

• 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；

• 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾；

• 以此类推，直到所有元素均排序完毕。

优点：

• 实现简单直观；

• 稳定性较好（虽然有些变种可能不是稳定的）。

4. 堆排序（Heap Sort）

介绍：

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

工作原理：

• 将待排序序列构造成一个大顶堆（或小顶堆）；

• 此时，整个序列的最大值（或最小值）就是堆顶的根节点；

• 将其与末尾元素进行交换，此时末尾就为最大值（或最小值）。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值（或次大值）。如此反复执行，便能得到一个有序序列了。

优点：

• 在平均和最好情况下，时间复杂度为O(nlogn)；

• 堆排序是不稳定的排序方法。

5. 快速排序（Quick Sort）

介绍：

快速排序是一种高效的排序算法，由英国计算机科学家C.A.R. Hoare在1960年提出。它的基本思想是采用分治策略，选取一个基准元素，通过一趟排序将待排序的数据分割成独立的两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行。

工作原理：

• 选择一个基准元素（pivot）；

• 通过一趟排序将待排序的数据分割成独立的两部分，左边部分的所有数据都小于基准元素，右边部分的所有数据都大于等于基准元素；

• 对左右两部分递归地应用快速排序。

优点：

• 速度快：平均时间复杂度为O(nlogn)，在大多数情况下表现出较高的效率。

• 效率高：原地排序算法，不需要额外的存储空间，只需对原始数组进行原地交换操作。

• 应用广泛：适用于各种数据类型的排序，包括数字、字符和对象等。

• 稳定性好：不会改变相同元素的原有顺序。

• 空间复杂度：O(logn)（递归栈空间），但在最坏情况下可能达到O(n)。

6. 归并排序（Merge Sort）

介绍：

归并排序是一种分治思想的排序算法。它将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

工作原理：

• 将待排序序列分成两个或更多的子序列，直到每个子序列只包含一个元素。

• 将两个或两个以上的有序表合并成一个新的有序表。

优点：

• 稳定性好：不会改变相同元素的原有顺序。

• 时间复杂度为O(nlogn)，是一种非常高效的排序算法。

7. 桶排序（Bucket Sort）

介绍：

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：首先，要使得数据分散得尽可能均匀；其次，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

工作原理：

• 设定一个定量的数组当作空桶子；

• 寻访序列，并且把项目一个一个放到对应的桶子去；

• 对每个不是空的桶子进行排序；

• 从不是空的桶子里把项目再放回原来的序列中。

优点：

• 当输入的数据可以均匀的分配到每一个桶中，排序的效率就会达到理想的状态。

8. 计数排序（Counting Sort）

介绍：

计数排序是一个非基于比较的排序算法，该算法于1954年由Harold H. Seward提出。它适用于一定范围内的整数排序，其复杂度为O(n+k)（其中k是整数的范围）。

工作原理：

• 找出待排序的数组中最大和最小的元素。

• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项。

• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）。

• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

优点：

• 当输入的数据是有确定范围的整数时，计数排序的效率会非常高。

缺点：

• 当k很大时，计数排序的空间复杂度会很高，且当O(k)＞O(n*log(n))时，其效率反而不如基于比较的排序算法。

• 计数排序只能用于整数排序，不能用于浮点数或字符串排序。

结语

Java中的排序算法种类繁多，每种算法都有其独特的优势和适用场景。在选择排序算法时，需要根据数据的规模、数据的特点以及具体需求来综合考虑。对于小规模数据，简单的排序算法如插入排序和选择排序可能更为方便；而对于大规模数据，快速排序、归并排序和堆排序则更为高效。此外，稳定性也是选择排序算法时需要考虑的一个重要因素。随着计算资源的不断丰富，并行化排序也成为了提高排序效率的一种有效手段。总之，在Java编程中，理解和掌握各种排序算法的原理和实现方式，对于提高程序的性能和效率至关重要。