乘法器的基本操作

顺序乘法的实现过程

案例

• 

• 在13 * 9 这个例子里面，被乘数13表示成二进制1101， 乘数9在二进制里面是1001

• 最右边的个位是 1，所以个位乘以被乘数，就是把被乘数 1101 复制下来

• 因为二位和四位都是 0，所以乘以被乘数都是 0，那么保留下来的都是 0000

• 乘数的八位是 1，我们仍然需要把被乘数 1101 复制下来

• 不过这里和个位位置的单纯复制有一点小小的差别，那就是要把复制好的结果向左侧移三位

• 然后把四位单独进行乘法加位移的结果，再加起来，我们就得到了最终的计算结果

顺序乘法器电路

• 

• 乘法因为只有“0”和“1”两种情况，所以可以做成输入输出都是 4 个开关，中间用 1 个开关，同时来控制这 8 个开关的方式，这就实现了二进制下的单位的乘法

• 

• 至于位移也不麻烦，我们只要不是直接连线，把正对着的开关之间进行接通，而是斜着错开位置去接就好了

• 如果要左移一位，就错开一位接线；如果要左移两位，就错开两位接线

顺序乘法器的优化

• 原因
  • 实际上，像 13×9 这样两个四位数的乘法，我们不需要把四次单位乘法的结果，用四组独立的开关单独都记录下来，然后再把这四个数加起来
  • 因为这样做，需要很多组开关，如果我们计算一个 32 位的整数乘法，就要 32 组开关，太浪费晶体管了
  • 如果我们顺序地来计算，只需要一组开关就好了
• 实现方式

  • 

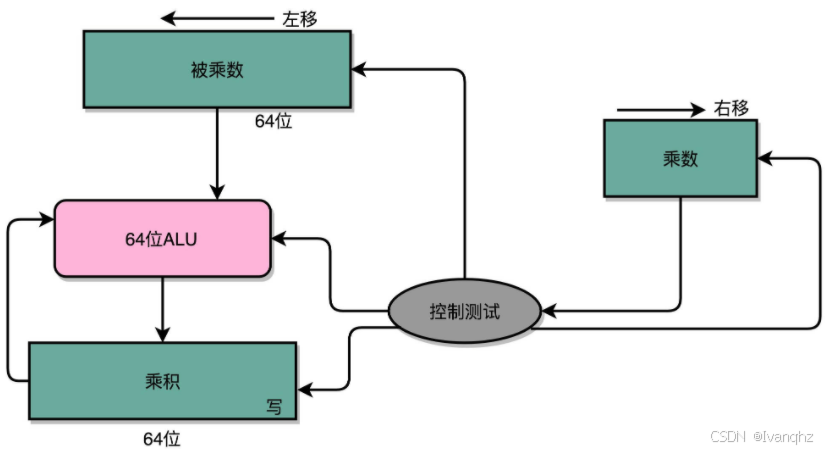
  • 我们先拿乘数最右侧的个位乘以被乘数，然后把结果写入用来存放计算结果的开关里面

  • 然后，把被乘数左移一位，把乘数右移一位，仍然用乘数去乘以被乘数，然后把结果加到刚才的结果上

  • 反复重复这一步骤，直到不能再左移和右移位置

  • 这样，乘数和被乘数就像两列相向而驶的列车，仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路，就能完成整个乘法

顺序乘法器的缺点

• 在这个乘法器的实现过程里，我们其实就是把乘法展开，变成了“加法 + 位移”来实现
• 的是 4 位数，所以要进行 4 组“位移 + 加法”的操作
• 而且这 4 组操作还不能同时进行
• 因为下一组的加法要依赖上一组的加法后的计算结果，下一组的位移也要依赖上一组的位移的结果
• 这样，整个算法是“顺序”的，每一组加法或者位移的运算都需要一定的时间
• 比如，这里的 4 位，就需要 4 次加法。而我们的现代 CPU 常常要用 32 位或者是 64 位来表示整数，那么对应就需要 32 次或者 64 次加法。比起 4 位数，要多花上 8 倍乃至 16 倍的时间

电路并行

遭遇的问题

• 门延迟（Gate Delay)
  • 位数越多，越往高位走，等待前面的步骤就越多，这个等待的时间有个专门的名词，叫作门延迟（Gate Delay）
  • 例子
    • 每通过一个门电路，我们就要等待门电路的计算结果，就是一层的门电路延迟，我们一般给它取一个“T”作为符号
    • 一个全加器，其实就已经有了 3T 的延迟（进位需要经过 3 个门电路）
    • 而 4 位整数，最高位的计算需要等待前面三个全加器的进位结果，也就是要等 9T 的延迟
    • 如果是 64 位整数，那就要变成 63×3=189T 的延迟。这可不是个小数字啊！
• 时钟频率
  • 在上面的顺序乘法计算里面，如果我们想要用更少的电路，计算的中间结果需要保存在寄存器里面
  • 然后等待下一个时钟周期的到来，控制测试信号才能进行下一次移位和加法，这个延迟比上面的门延迟更可观

解决方法

• 只要把进位部分的电路完全展开就好了

• 半加器到全加器，再到加法器，都是用最基础的门电路组合而成的

• 门电路的计算逻辑，可以像我们做数学里面的多项式乘法一样完全展开

• 在展开之后呢，我们可以把原来需要较少的，但是有较多层前后计算依赖关系的门电路，展开成需要较多的，但是依赖关系更少的门电路

• 

  • 类似于世界杯足球赛那样的淘汰赛，32 个球队捉对厮杀，同时开赛
  • 这样一天一下子就淘汰了 16 支队，也就是说，32 个数两两相加后，你可以得到 16 个结果
  • 后面的比赛也是一样同时开赛捉对厮杀。只需要 5 天，也就是 O(log2N) 的时间，就能得到计算的结果
  •