N皇后问题---线性方程处理

N皇后问题—线性方程处理

关键词：回溯 JavaScript

题目：

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

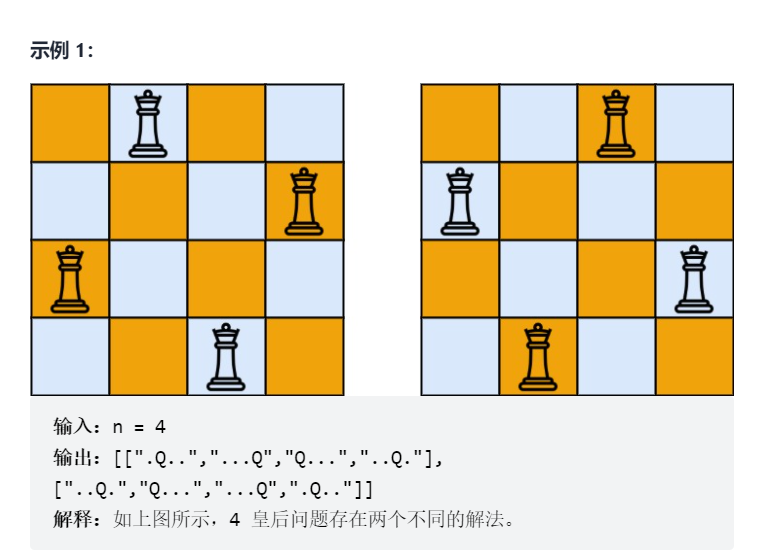
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens

解法分析

首先能够看出这是一个利用回溯处理的问题，每次尝试不同的选择，如果不合法就返回，选择其他的情况。

因为棋盘涉及横轴和纵轴都要进行选择，所以在回溯的迭代部分是一个二维的，需要用一个二维数组来记录中途保存的值。

这个二维数组的生成方法还是遇到了点麻烦，尝试了以下两种写法：

// 写法1
let path = new Array(n).fill(['.', '.', '.', '.']);
// 写法2 虽然赋值生成的新数组不再与pathitem关联，但是它们之间还是关联的
let path_item = ['.', '.', '.', '.'];
let path = new Array(n).fill([...path_item]);

这两种写法都没有避免存入path数组中的n个子数组是相关联的，即都是引用值传递，对一个的修改会进行传递。

参考了别人的写法：

// 这种写法将原本关联的数组 映射为每次新生成的新数组就不会关联了
let path = new Array(n).fill([]).map(() => new Array(n).fill('.'));
path[1] == path[2] // false

这里应该是map函数会对每个元素都调用一次赋值为新生成的数组从而导致它们之间变成彼此独立的。

我的理解是原本数组空间中存储的是子数组地址的引用值，现在将这个数组空间改成新子数组的引用值，然后每个索引对应的都是一个新子数组的引用值，它们彼此指向的子数组不相同，所以不会相互关联。

很明显可以想到使用一个行标志数组和列标志数组来记录已选择过的行和列来保证不重复：

let row_flag = new Array(n).fill(0);
let column_flag = new Array(n).fill(0);

对于斜线方向上的情况，可以看作一个坐标轴来处理：

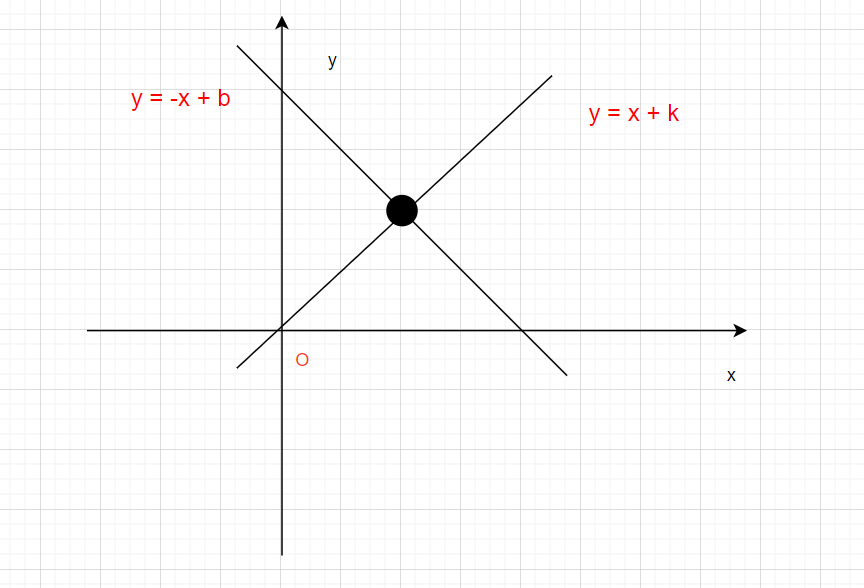
每个点对应棋盘上的斜线会分为两条，一条是45度的一条是135度的，

对于不同点来说斜率是相同的，只是偏移量不同，因此使用两个字典来分别存储已选点的正方向偏移量k和负方向偏移量b

 // 记录斜线使用 看作是线性方程 y = x+k和 y=-x+b，记录这里的k和b
let k_positive = new Map();
let k_negative = new Map();

这里不能使用一个字典来存储是因为一个点的正偏移可能等于另外一个点的负偏移，但它们其实并不在斜线上，这样的判断就会误判为它们不符合条件，影响结果。

k的计算：$k=y-x$ 来获取

b的计算：$-x+b=x+k$ => $b=2x+k$

// 45
let line_positive = y-x;
// 135
let line_negative = 2*x + line_positive;

对于字典的获取函数get()，0和undefined都会返回false；所以直接判断即可：

// 因为这个斜线可以分为两个方向，返回0或者undefined
if ((!k_positive.get(line_positive)) && (!k_negative.get(line_negative)))

然后选取后添加键值对，值为1，回溯时，将值改成0

只要一个点的正偏移和负偏移都没有在两个字典中出现过（因为斜率固定，正负偏移就分别确定了两条直线），那么它们在斜线上就没有重复。

其余部分就利用传统的回溯进行处理即可，注意对于行来说，只要记录行的起始位，每次从下一行取，就可以确保行不会重复，就不需要对行建立标志数组了。

 for(let y=start_y; y<n; y++)

代码：

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    let result = [];
    // 直接操作复制的是引用值，path数组模拟棋盘
    // let path = new Array(n).fill([...path_item]); 这样写不行，它们内部还是关联的
    
    // 这种写法将原本关联的数组 映射为每次新生成的新数组就不会关联了
    let path = new Array(n).fill([]).map(() => new Array(n).fill('.'));


    // 记录行使用，记录列使用. 不需要记录行，每次从下一行选就已经满足了不是同一行
    // let row_flag = new Array(n).fill(0);
    let column_flag = new Array(n).fill(0);

    // 记录斜线使用 看作是线性方程 y = x+k和 y=-x+b，记录这里的k和b
    let k_positive = new Map();
    let k_negative = new Map();
    // 将棋盘转过来看作坐标系
    // 棋盘上的点就是由线性方程 y = x+k和 y=-x+b 构成 k=y-x
    // 根据线性方程交于一点： x+k = -x+b =>  b=2x+k
    


    // used_num记录已经放置的皇后数量
    function backCombine(path, used_num, start_y){
        if (start_y >= n && used_num <n) return 
        if (used_num == n){
            // path数组的数据转化为满足输出条件的格式
            let res = [];
            for (let i=0; i<path.length; i++){
                res[i] = path[i].join('');
            }
            result.push(res);
            return;
        }
        // 要决定放哪一行还要决定这一行的那个列，所以是个二维的回溯
        for (let y=start_y; y<n; y++){
            for (let x=0; x<n; x++){
                if (column_flag[x] != 0) continue;
                // 45
                let line_positive = y-x;
                // 135
                let line_negative = 2*x + line_positive;
                // 因为这个斜线可以分为两个方向，返回0或者undefined
                if ((!k_positive.get(line_positive)) && (!k_negative.get(line_negative))){
                    // 取反向，跟视觉看起来一样
                    path[n-1-y][x] = 'Q';
                   
                   column_flag[x] = 1;
                    k_positive.set(line_positive, 1);
                    k_negative.set(line_negative, 1);
                    used_num++;
                    // console.log(path);
                    backCombine(path, used_num, y+1);
                    used_num--;                 
                    path[n-1-y][x] = '.';
                    column_flag[x] = 0;
                    k_positive.set(line_positive, 0);
                    k_negative.set(line_negative, 0);
                }
            }
        }
    }
    backCombine(path, 0, 0);
    return result;
};