poj 2728 最优比率生成树

Desert King

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 30394		Accepted: 8375

Description

David the Great has just become the king of a desert country. To win the respect of his people, he decided to build channels all over his country to bring water to every village. Villages which are connected to his capital village will be watered. As the dominate ruler and the symbol of wisdom in the country, he needs to build the channels in a most elegant way. 

After days of study, he finally figured his plan out. He wanted the average cost of each mile of the channels to be minimized. In other words, the ratio of the overall cost of the channels to the total length must be minimized. He just needs to build the necessary channels to bring water to all the villages, which means there will be only one way to connect each village to the capital. 

His engineers surveyed the country and recorded the position and altitude of each village. All the channels must go straight between two villages and be built horizontally. Since every two villages are at different altitudes, they concluded that each channel between two villages needed a vertical water lifter, which can lift water up or let water flow down. The length of the channel is the horizontal distance between the two villages. The cost of the channel is the height of the lifter. You should notice that each village is at a different altitude, and different channels can't share a lifter. Channels can intersect safely and no three villages are on the same line. 

As King David's prime scientist and programmer, you are asked to find out the best solution to build the channels.

Input

There are several test cases. Each test case starts with a line containing a number N (2 <= N <= 1000), which is the number of villages. Each of the following N lines contains three integers, x, y and z (0 <= x, y < 10000, 0 <= z < 10000000). (x, y) is the position of the village and z is the altitude. The first village is the capital. A test case with N = 0 ends the input, and should not be processed.

Output

For each test case, output one line containing a decimal number, which is the minimum ratio of overall cost of the channels to the total length. This number should be rounded three digits after the decimal point.

Sample Input

4
0 0 0
0 1 1
1 1 2
1 0 3
0

Sample Output

1.000

Source

Beijing 2005

最优比率生成树模板题

问题模型1

基本01分数规划问题

给定nn个二元组(valuei,costi)(valuei,costi)，valueivaluei是选择此二元组获得的价值（非负），costicosti是选择此二元组付出的代价（非负），设xi(xi∈{0,1})xi(xi∈{0,1})代表第ii个二元组的选与不选，最大(小)化下式 

maximize(or minimize)   r=∑valuei⋅xi∑costi⋅ximaximize(or minimize)   r=∑valuei⋅xi∑costi⋅xi

 

下面先说最大化

解决方法

二分法

设rr最大值为r∗r∗， 

r∗=∑valuei⋅xi∑costi⋅xir∗=∑valuei⋅xi∑costi⋅xi

 

 

∑valuei⋅xi−r∗⋅∑costi⋅xi=0∑valuei⋅xi−r∗⋅∑costi⋅xi=0

 

设一个函数，自变量为rr值， 

f(r)=∑valuei⋅xi−r∗⋅∑costi⋅xif(r)=∑valuei⋅xi−r∗⋅∑costi⋅xi

 

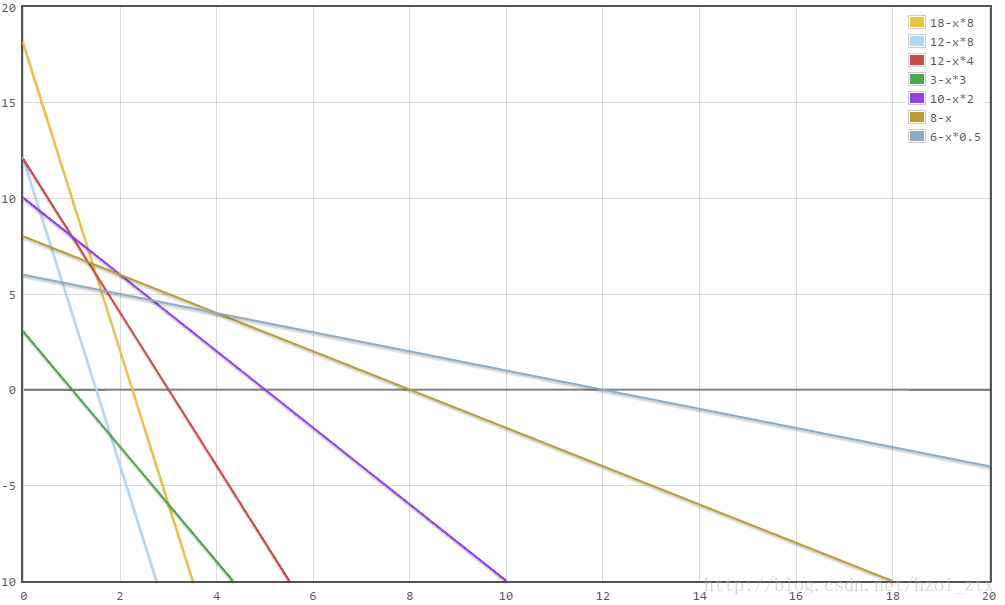
观察这个函数，假如{xi}{xi}固定，则这个函数就是坐标系中一条直线(y=B−A⋅xy=B−A⋅x)，每一组{xi}{xi}对应着一条直线，这些直线斜率非正(因为−A=−∑costi⋅xi≤0−A=−∑costi⋅xi≤0)，纵截距非负(因为B=∑valuei⋅xi≥0B=∑valuei⋅xi≥0 )，如图1。 

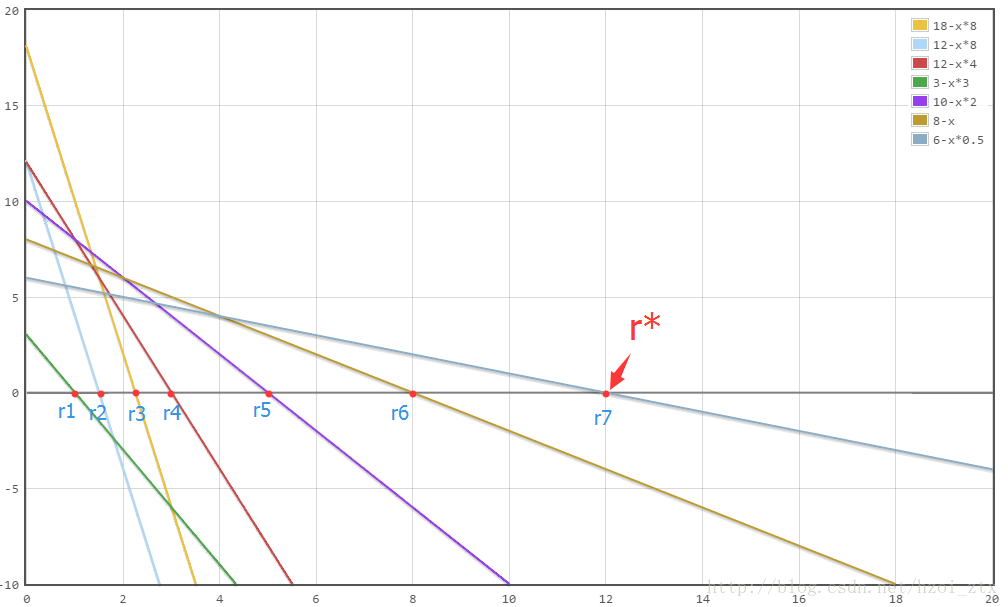
对于每一条直线，当f(r)=0f(r)=0时，横截距就是这一组的rr，那么r∗r∗就是每条直线横截距的最大值（每组{xi}{xi}对应rr的最大值）如图2。 

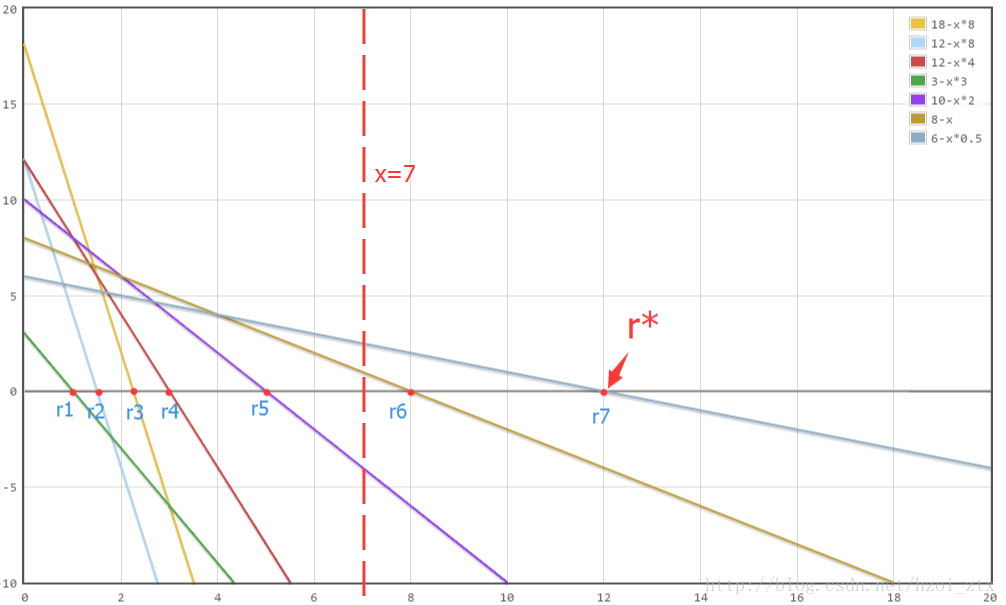
在图中上任取一条垂直xx轴的竖线， 
如果存在直线与这条竖线的交点纵坐标为正，那么最优值一定在当前竖线的右侧； 
如果所有直线与这条竖线交点纵坐标为负，那么最优值一定在当前竖线的左侧； 
如果所有直线与这条竖线交点纵坐标非正且存在直线与这条竖线交点纵坐标为0，那么当前竖线横坐标即为最优值r∗r∗。 

按照这个思想，可以二分答案rr，那么二分时如何进行判断呢？

选择一个rr时需要判断所有f(r)f(r)的最大值是否为0，如果max{f(r)}>0max{f(r)}>0则r<r∗r<r∗；如果max{f(r)}<0max{f(r)}<0 则 r>r∗r>r∗。 
怎样求max{f(r)}max{f(r)}? 

f(r)=∑valuei⋅xi−r⋅∑costi⋅xi=∑(valuei−r⋅costi)⋅xif(r)=∑valuei⋅xi−r⋅∑costi⋅xi=∑(valuei−r⋅costi)⋅xi

 

二分一个rr时，每个二元组的valuei−r⋅costivaluei−r⋅costi 都可以求出，设其为weightiweighti，现在的目标就是找到一组{xi}{xi}使得∑wighti⋅xi∑wighti⋅xi最大（即求max{f(r)}max{f(r)}）。怎么找到这一组{xi}{xi}，或者直接求得max{f(r)}max{f(r)}呢？具体问题具体分析，经常借助最短路算法判断是否存在负环。下面会有几道例题。

01分数规划还会与其他问题结合，如网络流等。

DinkelbachDinkelbach算法

这个算法我是在写这篇文章时才知道的。

思考上述二分算法的思路，设二分过程中某一个二分值为rr，二分时的判断条件是max{f(r)}max{f(r)}的正负性，而这个rr除了让LL右移或者RR左移就没有用了。现在思考某一过程中rr与max{f(r)}max{f(r)}能否再被利用。 
二分时，假如max{f(r)}>0max{f(r)}>0这说明最优解在当前rr的右侧，于是让L=rL=r，但是，如果将LL移动到max{f(r)}max{f(r)}对应直线的横截距呢？显然，算法会变得更快。这个思想就是DinkelbachDinkelbach算法的内涵。 
DinkelbachDinkelbach实质上是一种迭代算法，基于这样的思想：不去二分答案，而是先随便给定一个答案，然后根据更优的解（max{f(r)}max{f(r)}对应直线的横截距）不断移动答案，逼近最优解。理论上它比二分快些。 
在这个算法中，一般将rr初始化为00。

再说最小化

看上面的图，也很好理解，就是最左边的rr为r∗r∗，当前的rr确定时需要用到min{f(r)}min{f(r)}。 
如果min{f(r)}>0min{f(r)}>0，那么r<r∗r<r∗； 
如果min{f(r)}=0min{f(r)}=0，那么r=r∗r=r∗； 
如果min{f(r)}<0min{f(r)}<0，那么r>r∗r>r∗。

做题时认清哪个是valueivaluei，哪个是costicosti，再记住上面几张图，基本不会出错了。

两种算法的比较

DinkelbachDinkelbach算法的弊端就是需要保存解。这两个算法解决统一问题实际上都有可能快些。 
我觉着我一般还是用二分。。。。

例题

[POJ2976]Dropping tests

---

问题模型2

最优比率生成树

带权无向图GG， 对于图中每条边eiei， 都有valueivaluei和costicosti，现在求一棵生成树TT，最大（小）化∑valuei∑costi,ei∈T∑valuei∑costi,ei∈T

解决方法

套用01分数规划模型，如果ei∈Tei∈T则xi=1xi=1否则xi=0xi=0。

二分法

二分答案rr，边赋值weighti=valuei−r⋅costiweighti=valuei−r⋅costi，因为是生成树，边的数量确定，那么max{f(r)}max{f(r)}需要选取前|G|−1|G|−1大的weightiweighti，也就是求最大生成树，按最大生成树权值的正负性就可以二分了。最小化就求最小生成树。

DinkelbachDinkelbach算法

当前答案rr，边赋值weighti=valuei−r⋅costiweighti=valuei−r⋅costi，同样求最大生成树，找到max{f(r)}max{f(r)}对应的边集{xi}{xi}，也就是最大生成树的边集。对这个边集找横截距当做下一次答案。横截距是啥呢？ 

f(r)=B−A⋅rrr=0=B/A=∑valuei⋅xi∑costi⋅xif(r)=B−A⋅r=0r=B/Ar=∑valuei⋅xi∑costi⋅xi

最小化就求最小生成树。

 

例题

[POJ2728]Desert King

以上内容来自：https://blog.csdn.net/hzoi_ztx/article/details/54898323

迭代：360ms

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
#define LL long long
#define N 1005
#define esp 1e-6
#define inf 1e10
struct P
{
    double x,y;
    double h;
}a[N];

int n;

double dis(int i,int j)
{
    double xx=(a[i].x-a[j].x)*(a[i].x-a[j].x);
    double yy=(a[i].y-a[j].y)*(a[i].y-a[j].y);
    return sqrt(xx+yy);
}

double dist[N];
int vis[N];
double C[N][N];
double D[N][N];
double d[N][N];
int pre[N];

void creat(double r)
{
    for(int i=1;i<=n;i++)
    {
        for(int j=i;j<=n;j++)
        {
            C[i][j]=C[j][i]=fabs(a[i].h-a[j].h);
            D[i][j]=D[j][i]=dis(i,j);
            d[i][j]=d[j][i]=C[i][j]-r*D[i][j];
        }
    }
}

double Prim(int star,double r)
{
    double scost=0,sdist=0;
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)
    {
        dist[i]=d[star][i];
        pre[i]=star;
    }
    dist[star]=0;
    vis[star]=1;
    int next;
    double m;
    int cnt=1;

    while(cnt<n)
    {
        m=inf;
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&dist[i]<m)
            {
                m=dist[i];
                next=i;
            }
        }
        scost+=C[pre[next]][next];
        sdist+=D[pre[next]][next];
        vis[next]=1;
        cnt++;
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&d[next][i]<dist[i])
            {
                dist[i]=d[next][i],pre[i]=next;
            }
        }
    }
    return scost/sdist;

}
int main()
{
     while(cin>>n&&n)
     {
         for(int i=1;i<=n;i++)
         {
             scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].h);
         }
         double now=0;
         while(1)
         {
             creat(now);
             double ans=Prim(1,now);
             if(fabs(ans-now)<=1e-6)break;
             now=ans;
             //cout<<l<<" "<<r<<endl;
         }
         printf("%.3f\n",now);
     }
}
/*
4
0 0 0
1 2 5
3 5 8
4 5 2
*/

二分：1900ms

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
#define LL long long
#define N 1005
#define esp 1e-6
#define inf 1e10
struct P
{
    double x,y;
    double h;
}a[N];

int n;

double dis(int i,int j)
{
    double xx=1.0*(a[i].x-a[j].x)*(a[i].x-a[j].x);
    double yy=1.0*(a[i].y-a[j].y)*(a[i].y-a[j].y);
    return sqrt(xx+yy);
}

double d[N][N];


double dist[N];
int vis[N];
double Prim(double r)
{
    double ans=0;
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)dist[i]=fabs(a[1].h-a[i].h)-r*dis(1,i);
    dist[1]=0;
    vis[1]=1;
    int next;
    double m;
    int cnt=1;
    while(cnt<n)
    {
        m=inf;
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&dist[i]<m)
            {
                m=dist[i];
                next=i;
            }
        }
        ans+=dist[next];
        vis[next]=1;
        cnt++;

        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&fabs(a[next].h-a[i].h)-r*dis(next,i)<dist[i])dist[i]=fabs(a[next].h-a[i].h)-r*dis(next,i);
        }
    }
    //cout<<"ans="<<ans<<endl;
    return ans;
}
int main()
{
     while(cin>>n&&n)
     {
         for(int i=1;i<=n;i++)
         {
             scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].h);
         }
         double l=0.0,r=1000.0;
         int cnt=13;
         while(r-l>1e-6)
         {
             double m=(l+r)/2;
             double ss=Prim(m);
             if(ss>=0)l=m;
             else r=m;
             //cout<<l<<" "<<r<<endl;
         }
         printf("%.3f\n",l);
     }
}