【密码学】Shamir密码分享原理，及其同态加性和同态乘性

【什么是Shamir秘密分享】
Alice希望向n个参与方分享一个秘密值s，任何t个参与方可以利用他们的分片恢复出密码值，但少于t个参与方无法得到s有关的信息。t被称为门限值，一个包含n个参与方且门限值为t的秘密分享被表示为(t,n)-秘密分享

【多项式模型】
随机构造一个t-1次多项式f(x):


这时候对于一个t个未知数的多项式，我们直到了包含其的t条方程，可以把所有未知数解出来。

这里我们直接用拉格朗日插值公式（t-1次方程，t个未知数，知道t组(x,y)就可以恢复原方程）

得到：

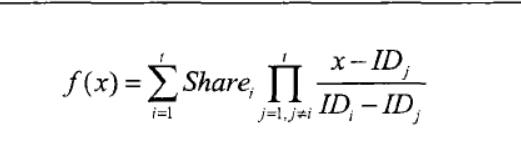
为什么这个是对的呢？首先它无疑是一个最高此为t-1的多项式
然后我们不妨考虑以下ID(k)的值，由于连乘号的存在，所以如果i不为k的话，j总是可以取到k，这样连乘部分必定为0.因此，为了得到非0项，我们必须使i=k
i = k的话，前半部分就是Share(k),而后半部分分资坟墓都是ID(k) - ID(j)所以恒为1
因此对于f(x)来说都有f(ID(k)) = Share(k)
也就验证了它的正确性
最后s就是f(0)

【Shamir多项式原理】
原理就是t-1次多项式有t个未知数，必须要用t个方程才可以解开

【Shamir的同态性】
1.同态加性：天然具有加法同态，如果多个(t,n)-Shamir秘密分享得到多个秘密值，那么不同秘密值得分片相加是对应秘密值和得分片（门限不变）
这个理解起来也很简单，就是多个f1,f2,…全部加起来，还是一个t-1次方程，t个未知数，但f(0)变成了s1 + s2 +…

2.同态乘性：受限的乘法同态性，如果d个(t,n)-Shamir分享多个秘密值，那么这若干个f1,f2…fd乘起来最高次就是d(t-1) 加上常数项共有d(t-1) + 1 个未知数
因此，如果d(t-1) + 1 > n显然n个人全部一起来都无法恢复
所以必须要满足d(t-1) + 1 <= n才有可能恢复秘密值的乘积
也就是说Shamir秘密分享有d阶乘法同态性必须满足上述不等式