Matlab有关矩阵的函数eig，diag，linspace，inv，randn，sort，冒号，std2，ksdensity，plot，cosd

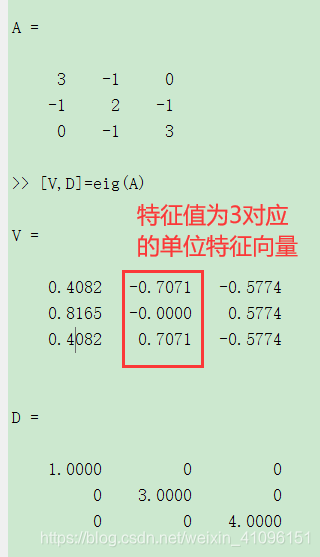
eig——特征值和特征向量

[V，D]=eig(A);
矩阵D对角线元素是特征值，矩阵V的列是右特征向量。什么是右特征向量？
D 中的特征值对应于 V 的各列中的特征向量

diag——提取对角线元素

diag(A)
提取矩阵A对角线上的元素，返回一个列向量

linspace——生成线性间距向量

例如
theta=linspace(-pi/2,pi/2,2000);
意思是，生成在-pi/2到pi/2之间2000个等间距点的行向量

inv——矩阵求逆

C=inv®;%计算方阵R的逆矩阵

randn——正太分布的随机数

S=randn(length(S),L);
返回一个从标准正态分布中得到的随机标量。
randn(3,4) 返回一个 3×4 的矩阵。矩阵元素由正太分布的随机数组成

sort——对数组元素排序

[Sp_rand,I]=sort(Sp,‘descend’);

Sp是列向量

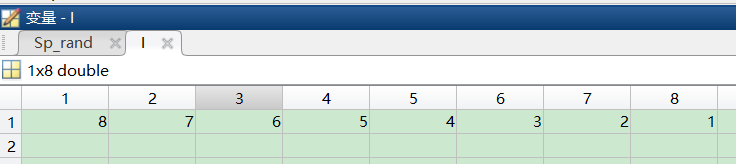
变量I是索引，变量Sp_rand是按降序（descent）排列的向量

• sort(A,2);对矩阵A按列排序，即从左到右排序列，第一列，第二列…

冒号

用于创建向量，下标数组，指定迭代。

• 指定迭代
• 创建下标数组，即创建索引向量，用来遍历数组，选择数组的行和列
  A(：，j)——A的第j列
  A(i ，：)——A的第i行
  A(j：k)——A(j)，A(j+1)，…，A(k)
  A(：，j：k)——A(：，j)，A(：，j+1)，…，A(：，k)
  逗号分隔，不是分号A(：， j)

A（j）


A(1:5)的结果是一个行向量

std2——计算标准差

标准差又称均方差，标准差是方差的算术平方根。标准差可以反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。标准差越小，表明数据越聚集；标准差越大，表明数据越离散。

ksdensity

方差能很好的解释一维数据的分布特性
方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法。标准差为方差的算术平方根。方差相应的计算公式为：

协方差矩阵

对于二维的数据，协方差矩阵

X与Y的相关性和Y与X的相关性是一样的，即σ(x,y)=σ(y,x)
协方差矩阵始终是一个对称阵，其对角线上的是方差，非对角线上的是协方差。
对协方差进行特征分解，得到特征值构成的矩阵和特征向量构成的矩阵
二维情况下有两个特征值和两个特征向量

plot

D是一个二维矩阵，
D（1，：）是横坐标值，D（2，：）纵坐标值，线型*

• plot（D（1，：），D（2，：），’ * '）

MATALAB将矩阵的每一列数据绘成单独的线条，矩阵的每一列数据看成一个向量。

cosd——参数以度为单位的余弦。

此 MATLAB 函数 返回 X 的元素的余弦（以度为单位）。
Y = cosd(X)