一、树的基本概念
树是一种非线性存储结构,存储具有“一对多”关系的数据元素集合
1. 树的特点
- 每个节点有零个或多个子节点
- 没有父节点的节点被称为根节点,每个树有且仅有一个根节点
- 每一个非根节点有且只有一个父节点
- 除根结点外,每个子节点可以分为多个不相交的子树
2. 树的相关概念
- 节点深度:根节点到x节点的路径长度
- 节点高度:叶子节点到x节点的路径长度
- 树的深度:结点的最大深度成为树的深度
- 父节点:若一个节点含有子节点,这个节点就称为子节点的父节点
- 子节点:一个节点含有的子数的根节点称为该节点的子节点
- 度:节点的子树数目称为节点的度
- 叶子结点:度为0的节点
- 节点的层次:从根节点开始,根节点为第一次,根节点的子节点为第二层,以此类推
3. 树的分类
- 二叉树:每个节点最多有两个子节点
- 多路查找树:每个节点有两个以上的子节点
二、二叉树
1. 二叉树的分类
a. 满二叉树
叶子结点都集中于二叉树的最底层
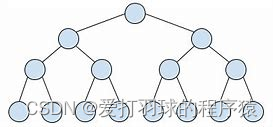
b. 完全二叉树
叶子结点只会出现在层次最大的两层上,且对于最大层次的叶子结点,都依次排列在该层最左边的位置
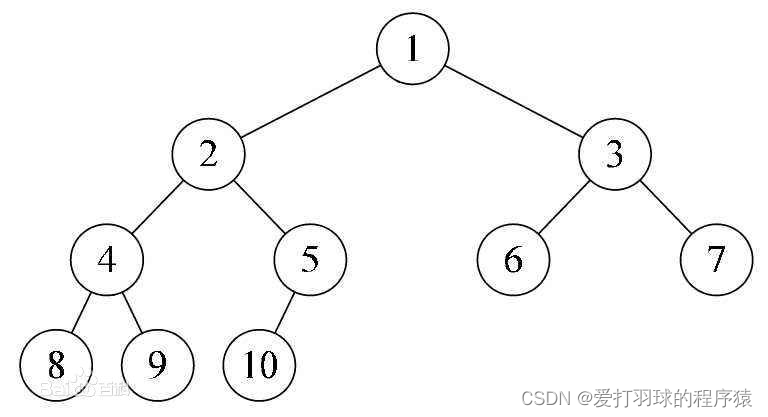
c. 二叉搜索树
左子树上所有节点的值都小于根节点,右子树上所有节点的值都大于根节点,左右子树各自又是一颗二叉搜索树
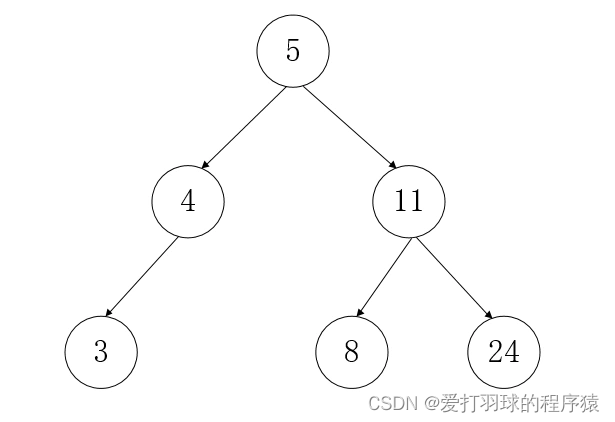
d. 平衡二叉搜索树
一种特殊的二叉搜索树,任意节点的左右子树深度之差不超过1
e. 红黑树
一种自平衡的二叉搜索树,在原有的平衡二叉搜索树基础上要求:
- 每个节点或者是黑色或者是红色
- 根节点为黑色
- 每个叶子节点是黑色(这里的叶子节点,是指为null的叶子节点)
- 一个节点为红色,它的子节点必须是黑色
- 任意一个节点到每个叶子节点的路径都包含相同数量的黑节点

2. 二叉树的性质
- 任意一棵树,节点数量为n,则边的数量为n - 1
- 非空二叉树上的叶子节点等于度为2的节点数加1:n0 = n2 + 1
- 非空二叉树第k层上最多有2 ^ (k-1)个节点(k >= 1)
- 高度为h的二叉树最多有2 ^ h - 1个节点(h >= 1)
- 对完全二叉树按从上到下,从左到右的顺序依次编号1,2,3…n,则有以下关系
- i > 1时,节点 i 的父节点编号为 i / 2,i 为偶数时,节点 i 为左子节点;i 为奇数时,节点i为右子节点
- 当2i < n是,节点i的左子节点为2i,否则无左子节点
- 当2i + 1 < n时,节点i的右子节点为2i + 1,否则无右子节点
- 具有n(n > 0)个节点的完全二叉树的高度为 ⌊log2n⌋+1,⌊log2n⌋ 表示取小于 log2n 的最大整数
3. 二叉树的存储
- 顺序存储:用一组地址连续的存储单元一次自上而下、自左而右存储二叉树的节点元素(一般是数组形式)
- 链式存储:二叉树每个节点最多有两个子节点,用一个数据域和两个指针域表示每个节点
4. 二叉树的遍历
- 前序遍历 vs 中序遍历 vs 后续遍历

前序遍历实现:
// 定义二叉树节点
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
// 前序遍历
public void preOrder(TreeNode root){
// 基于递归实现
List<Integer> preRecur = new ArrayList<>();
preOrderRecur(root, preRecur);
// 基于非递归实现
List<Integer> preNonRecur = new ArrayList<>();
preOrderNonRecur(root, preRecur);
}
// 前序遍历的递归实现
public void preOrderRecur(TreeNode node, List<Integer> res){
if(null == node){
return;
}
res.add(node.val);
preOrderRecur(node.left, res);
preOrderRecur(node.right, res);
}
// 前序遍历的非递归实现
// 借助栈,先存右节点,再存左节点(由于栈是先进后出,先要左节点,就后压入左节点),先进后出即可实现前序
public void preOrderNonRecur(TreeNode node, List<Integer> res){
if(null == node){
return;
}
Stack<TreeNode> stack = new Stack<>();
stacl.push(node);
while(!stack.empty()){
TreeNode cur = stack.pop();
res.add(cur.val);
if(null != cur.right){
stack.push(cur.right);
}
if(null != cur.left){
stack.push(cur.left);
}
}
}
中序遍历实现:
// 定义二叉树节点
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
// 中序遍历
public void midOrder(TreeNode root){
// 基于递归实现
List<Integer> preRecur = new ArrayList<>();
midOrderRecur(root, preRecur);
// 基于非递归实现
List<Integer> preNonRecur = new ArrayList<>();
midOrderNonRecur(root, preRecur);
}
// 中序遍历的递归实现
public void midOrderRecur(TreeNode node, List<Integer> res){
if(null == node){
return;
}
midOrderRecur(node.left, res);
res.add(node.val);
midOrderRecur(node.right, res);
}
// 中序遍历的非递归实现
// 借助栈,先一直将当前节点的左节点压入栈,直至没有左节点就弹出,弹出节点有右节点,则将右节点压入栈,循环实现中序遍历
public void midOrderNonRecur(TreeNode node, List<Integer> res){
if(null == node){
return;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode temp = node;
while(!stack.empty() || null != temp){
if(null != temp){
// 持续将左节点压入栈中,直至没有左节点
stack.push(temp);
temp = temp.left;
} else {
// 栈顶弹出节点,若该节点有右节点,则下个循环将该节点的右节点压入栈
temp = stack.pop();
res.add(temp.val);
temp = temp.right;
}
}
}
后续遍历实现:
// 定义二叉树节点
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
// 后序遍历
public void postOrder(TreeNode root){
// 基于递归实现
List<Integer> preRecur = new ArrayList<>();
postOrderRecur(root, preRecur);
// 基于非递归实现
List<Integer> preNonRecur = new ArrayList<>();
postOrderNonRecur(root, preRecur);
}
public void postOrderRecur(TreeNode node, List<Integer> res){
if(null != node){
return;
}
postOrderRecur(node.left, res);
postOrderRecur(node.right, res);
res.add(node.val);
}
// 后序遍历非递归实现
// 借助栈,存储前序遍历结果(但先压入左节点,后压入右节点),列表存储每次前一个栈弹出的节点
// 列表元素逆序结果,就是后序遍历结果
public void postOrderNonRecur(TreeNode node, List<Integer> res){
if(null != node){
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(node);
while(!stack.empty()){
TreeNode cur = stack.pop();
res.add(cur.val);
if(null != cur.left){
stack.push(cur.left);
}
if(null != cur.right){
stack.push(cur.right);
}
}
// 列表逆序
Collections.reverse(res);
}
- 层序遍历

// 定义二叉树节点
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public void levelOrder(TreeNode root, List<Integer> res){
if(null == root){
return;
}
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while(queue.isEmpty()){
TreeNode cur = queue.poll();
res.add(cur.val);
if(null != cur.left){
queue.offer(cur.left);
}
if(null != cur.right){
queue.offer(cur.right);
}
}
}
public void levelOrder(TreeNode root, List<List<Integer>> res){
if(null == root){
return;
}
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while(queue.isEmpty()){
List<Integer> subRes = new ArrayList<>();
int count = queue.size();
for(int i = 0; i < count; i++){
TreeNode cur = queue.poll();
subRes.add(cur.val);
if(null != cur.left){
queue.offer(cur.left);
}
if(null != cur.right){
queue.offer(cur.right);
}
}
res.add(subRes);
}
}
5. 平衡二叉树的平衡调整
-
LL型 – 单向右旋平衡处理:在A的左子节点(L)的左子树(L)上插入新节点,需要进行一次右向顺时针旋转

-
RR型 – 单向左旋平衡处理:在A的右子节点®的右子树®上出入新节点,需要进行一次左向逆时针旋转

-
LR型 – 双向旋转(先左后右)平衡处理:在A的左子节点(L)的右子树®上插入新节点

-
RL型 – 双向旋转(先右后左)平衡处理:在A的右子节点®的左子树(L)上插入新节点

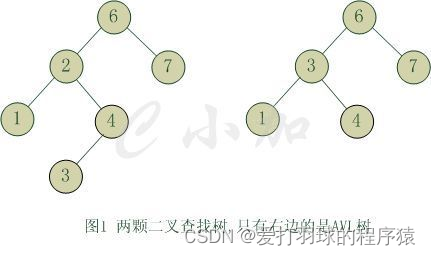
6. 平衡二叉树 vs 红黑树
- 平衡二叉树通过保持任一节点左、右子树高度差的绝对值不超过1来维持二叉树的平衡;而红黑树是根据查找路径上黑色节点的个数以及红、黑节点之间的联系来维持二叉树的平衡
- 平衡二叉树在插入或者删除节点时为了保证左右子树的高度差会进行旋转,这一个旋转根据数据的不同旋转的复杂度也会不一样,所以在插入或者删除平衡二叉树的节点时,旋转的次数不可知,这也导致在频繁的插入、修改中造成的效率问题;红黑树在执行插入修改的操作时会发生旋转与变色(红变黑,或者黑变红)以确保没有一条路径会比其它路径长出两倍,每次插入最多只需要三次旋转就能达到平衡。
- 总体来说,在插入或者删除节点时,红黑树旋转的次数比平衡二叉树少,因此在插入与删除操作比较频繁的情况下,选用红黑树。
三、多路查找树
1. 二叉树 vs 多路查找树
- 在海量节点的情况下,构建二叉树需要多次进行I/0操作(往返每个节点意味着需要在硬盘的页面之间进行访问),同时二叉树的高度很大
- 多路查找树允许每个节点可以有更多的数据项和更多的子节点
- 多路查找树包括:2-3树、2-3-4树、B树、B+树,B*树,它们都是平衡搜索树,且所有叶子结点都在同一层
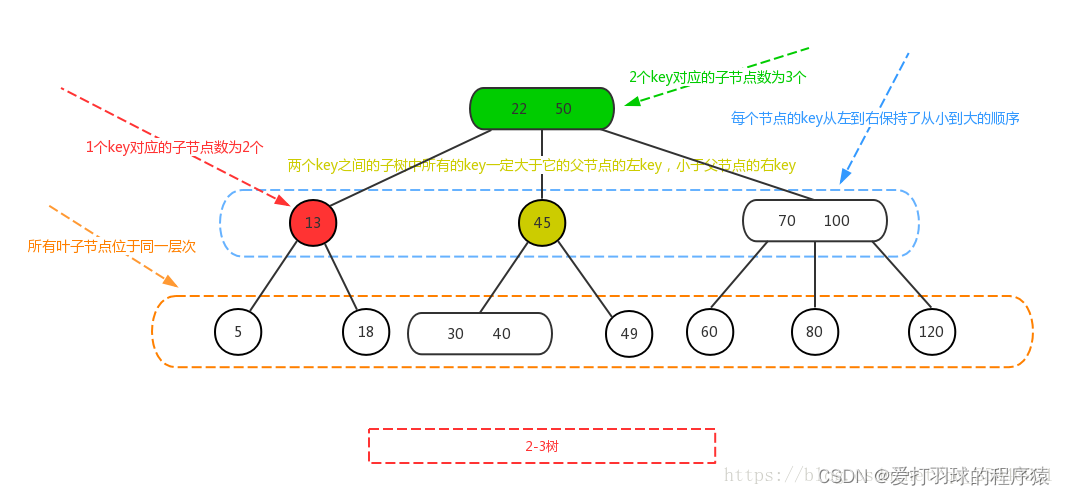
2. 2-3树
- 所有叶子结点都在同一层
- 一个二节点包含一个元素和两个子节点,左子树包含的元素小于该元素,右子树包含的元素大于该元素。二节点要么没有孩子,要么就有两个。
- 一个三节点包含一小一大两个元素和三个子节点,左子树包含小于较小元素的元素,右子树包含大于较大元素的元素,中间子树包含介于两元素之间的元素。三节点要么没有孩子,要么有三个孩子。
- 2-3树是由二节点和三节点构成的树
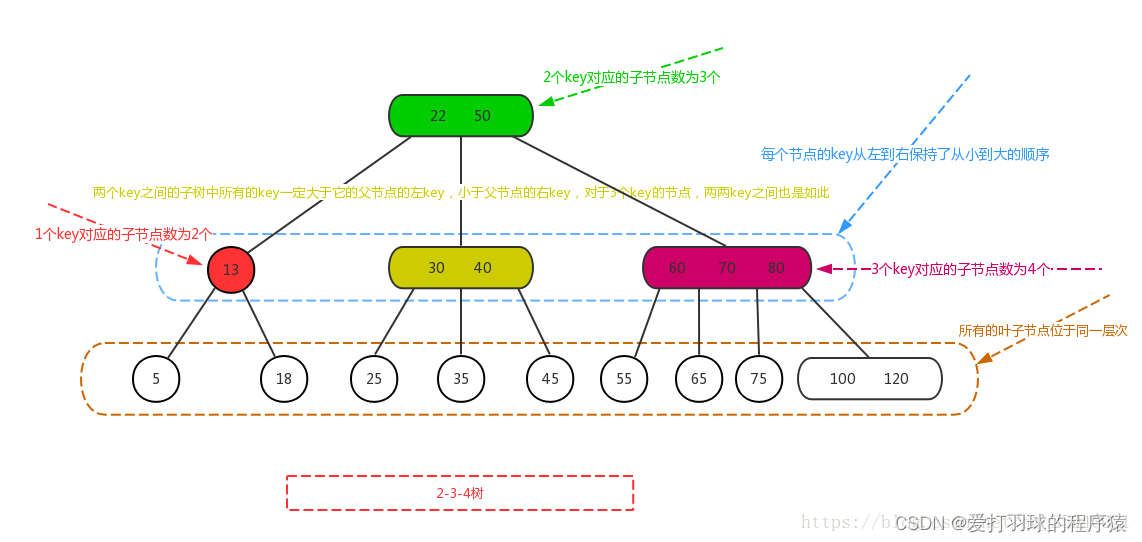
3. 2-3-4树
- 2-3-4树是在2-3树的基础上进行拓展,除了二节点和三节点,还包含四节点
- 一个四节点包含小中大三个元素和四个子节点,左子树包含小于最小元素的元素,第二子树包含大于最小元素小于第二元素的元素,第三子树包含大于第二元素小于最大元素的元素,右子树包含大于最大元素的元素
4. B树
- 一种平衡的多路查找树,2-3树和2-3-4树都是B树的特例。
- 节点最大的子节点数目成为B树的阶,2-3树是3级B数,2-3-4数是4级B树
- 对于一个m阶B树
- 如果根节点不是叶子结点,则至少有两个子树
- 每一个非根分支节点(非叶子结点),都有k-1个元素和k个孩子;每一个叶子结点都有k - 1个元素。其中,m/2 < k < m
- 所以叶子结点都位于同一层次
- 所有分支节点(非叶子结点)包含(n,A0,K1,A1,K2,A2,…Kn,An),其中:
- n为结点中的元素个数,
- Ki < Ki+1(i = 1,2,…,n)
- Ai(i = 0,1,2,…,n)为指向子树根节点的指针
- 指针Ai-1所指子树中的所有结点的关键字均小于Ki(i=1,2,…,n)
- An所指子树中的所有关键字均大于Kn

5. B+树
- B树的缺陷
- 在B树中,往返每个节点意味着需要在硬盘的页面之间进行多次访问。
- 遍历下面的B树,其中每个节点属于硬盘的不同页面,中序遍历所有元素就需要访问:页面2->页面1->页面3->页面1->页面4->页面1->页面5。
- 每次经过父节点都需要进行一次遍历

- B+树在B树的基础上进行了改进。
- B树中,每一个元素在B树中只出现一次,有可能在叶子节点,也可能在分支节点。
- 在B+树中,出现在分支节点中的元素会在叶子结点中再次列出。同时每一个叶子结点都会保存一个指向后一个叶子结点的指针。
- B+树只可能在叶子节点命中被查询的关键,不能在非叶子节点命中。非叶子节点相当于是叶子节点的索引,称为稀疏索引。
- B+树更适合文件系统

- B树和B+树的区别
- 有n棵子树的节点包含有n个关键字
- 所有的叶子结点包含全部关键字的信息,叶子结点本身按照关键字的大小自小到大顺序链接
- 所有分支节点可以看成索引,节点中仅含有其子树中的最大(或最小)关键字
6. B*树
- B*树是B+树的变体,在B+树的非根和非叶子结点在增加指向兄弟的指针

- B+树和B*树的区别:
- B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3,代替B+树的(1/2)M,M代表层数
- B+树的分裂:
- 当一个节点满时,分配一个新的节点,将原节点中1/2的数据复制到新节点,最后在父节点中增加新节点的指针;
- B+树的分裂只影响源节点和父节点,不影响兄弟节点,所以不指向兄弟的指针
- B*树的分裂:
- 当一个节点满时,如果它的下一个兄弟节点未满,那么将一部分数据移到兄弟节点中,再在源节点插入关键字,最后修改父节点中兄弟节点的关键字(因为兄弟结点的关键字范围改变了);
- 如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
- B*树分配新结点的效率比B+树要低,但空间使用率更高;






















 242
242











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








