二 图

于 2018-06-26 20:21:13 发布
阅读量470 收藏
点赞数

此文章参考了多个博客，不一一列举了，并且里面有一部分是自己写的

一、基本术语

图：由有穷、非空点集和边集合组成，简写成G(V,E);

Vertex：图中的顶点；


无向图：图中每条边都没有方向；

有向图：图中每条边都有方向；


无向边：边是没有方向的，写为(a,b)

有向边：边是有方向的，写为<a,b>

有向边也成为弧；开始顶点称为弧尾，结束顶点称为弧头；


简单图：不存在指向自己的边、不存在两条重复的边的图；


无向完全图：每个顶点之间都有一条边的无向图；

有向完全图：每个顶点之间都有两条互为相反的边的无向图；


稀疏图：边相对于顶点来说很少的图；

稠密图：边很多的图；


权重：图中的边可能会带有一个权重，为了区分边的长短；

网：带有权重的图；


度：与特定顶点相连接的边数；

出度、入度：对于有向图的概念，出度表示此顶点为起点的边的数目，入度表示此顶点为终点的边的数目；


环：第一个顶点和最后一个顶点相同的路径；

简单环：除去第一个顶点和最后一个顶点后没有重复顶点的环；


连通图：任意两个顶点都相互连通的图；

极大连通子图：包含竟可能多的顶点（必须是连通的），即找不到另外一个顶点，使得此顶点能够连接到此极大连通子图的任意一个顶点；

连通分量：极大连通子图的数量；

强连通图：此为有向图的概念，表示任意两个顶点a，b，使得a能够连接到b，b也能连接到a 的图；


生成树：n个顶点，n-1条边，并且保证n个顶点相互连通（不存在环）；

最小生成树：此生成树的边的权重之和是所有生成树中最小的；


AOV网：结点表示活动的网；

AOE网：边表示活动的持续时间的网；


二、图的存储结构


1.邻接矩阵


维持一个二维数组，arr[i][j]表示i到j的边，如果两顶点之间存在边，则为1，否则为0；

维持一个一维数组，存储顶点信息，比如顶点的名字；

下图为一般的有向图：


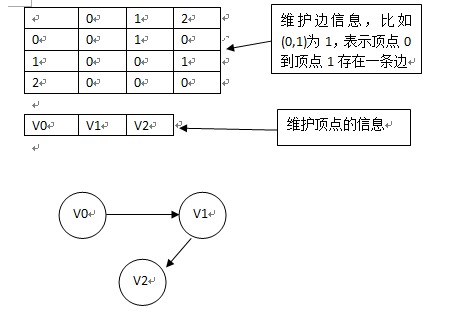
注意：如果我们要看vi节点邻接的点，则只需要遍历arr[i]即可；


 下图为带有权重的图的邻接矩阵表示法：

 

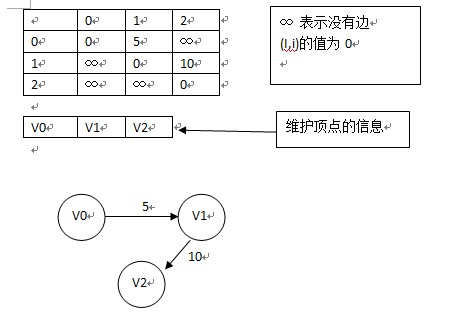
缺点：邻接矩阵表示法对于稀疏图来说不合理，因为太浪费空间； 

//1、邻接矩阵--用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中边或弧的信息  
//邻接矩阵存储结构代码   
    typedef char VertexType;//顶点类型由用户定义  
    typedef int EdgeType;//边上的权值类型由用户定义  
#define MAXVEX 100 //最大顶点数  
#define INFINITY 65535 //用65535来代表无穷大  
typedef struct  
{  
    VertexType vexs[MAXVEX];//顶点表  
    EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵，可看做边表  
    int numVertexes, numEdges;//图中当前的顶点数和边数  
    }MGraph;  

//无向网图的邻接矩阵创建  
void CreateMGraph(MGraph *G)  
{  
    int i, j, k, w;  
    printf("输入顶点数和边数：\n");  
    scanf("%d,%d", &G->numVertexes, &->numEdges);//输入顶点数和边数  
    for (i = 0; i < G->numVertexes; i++)  
        scanf("%c",&G->vexs[i]);  
    for (i = 0; i < G->numVertexes; i++)  
        for (j = 0; j < numVertexes; j++)  
        {  
            G->arc[i][j] = INFINITY;  
            G->arc[i][i] = 0;  
        }//邻接矩阵初始化  
    for (k = 0; k < G->numEdges; k++)//读入numEdges条边，建立邻接矩阵  
    {  
        printf("输入边（vi,vj)上的下标i,下标j和权w:\n");  
        scanf("%d,%d,%d", &i, &j, &w);  
        G->arc[i][j] = w;  
        G->arc[j][i] = G->arc[i][j];//因为图为无向图，所以矩阵对称  
    }  
}

2.邻接表


如果图示一般的图，则如下图：


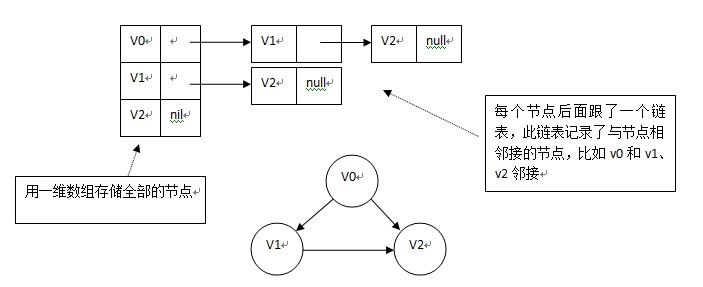
 如果是网，即边带有权值，则如下图：



//2、邻接表---数组与链表相结合、无向图的存储方法（关注顶点更方便）  
/*图的邻接表存储的结构代码*/
typedef char VertexType;//顶点类型
typedef int EdgeType;//边上的权值类型
#define MAXVEX 100//最大顶点数
typedef struct EdgeNode //边表结点
{
	int adjvex;//邻接点域，存储该顶点对应的下标
	EdgeType weight;//用于存储权值，对于非网图可以不需要
	struct EdgeNode *next;//链域，指向下一个邻接点
}EdgeNode;
typedef  struct VertexNode  //顶点表结点
{
	VertexType data;//顶点域，存储顶点信息
	EdgeNode *firstedge;//边表头指针
}VertexNode,AdjList[MAXVEX];
typedef struct
{
	AdjList adjList;
	int numVertexes, numEdges;//图中当前顶点数和边数
}GraphAdjList;

//无向网图的邻接表创建  
void CreatALGraph(GraphAdjList *G)  
{  
    int i, j, k;  
    EdgeNode *e;  
    printf("输入顶点数和边数：\n");  
    scanf("%d,%d", &G->numVertexes, &->numEdges);//输入顶点数和边数)  
    for (i = 0; i < G->numVertexes; i++)//读入顶点信息，建立顶点表  
    {  
        scanf(&G->adjList[i].data);  
        G->adjList[i].firstedge = NULL;//先将边表初始化为空表  
    }  
    for (k = 0; k < G->numEdges; k++)//建立边表  
    {  
        printf("输入边（vi,vj)上的顶点序号：\n");  
        scanf("%d,%d", &i, &j);  
        e = (EdgeNode*)malloc(sizeof(EdgeNode));//向内存申请空间生成边表结点  
        e->adjvex = j;//邻接序号为j  
        e->next = G->adjList[i].firstedge;  
        G->adjList[i].firstedge = e;//头插法  
  
        e = (EdgeNode*)malloc(sizeof(EdgeNode));//向内存申请空间生成边表结点  
        e->adjvex = i;//邻接序号为i  
        e->next = G->adjList[j].firstedge;  
        G->adjList[j].firstedge = e;//头插法  
    }  
 }  
//3、十字链表--既能表示出度又能表示入度，有向图的存储方法  
//4、邻接多重表--更关注边，无向图的存储方法  
//5、边集数组--更适合对边的操作
3.边集数组

适合依次对边进行操作；

存储边的信息，如下图：


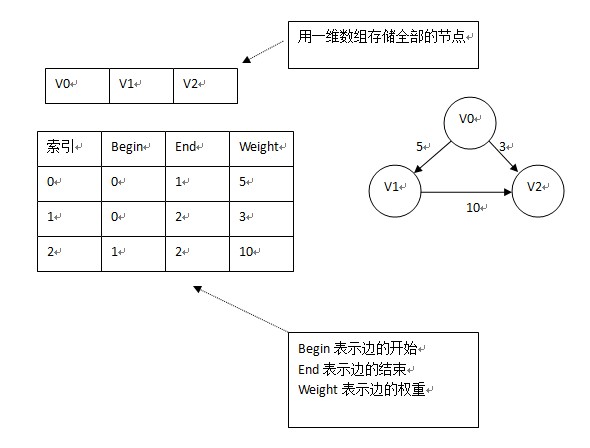
三、图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次

DFS（深度优先遍历）

思想：往深里遍历，如果不能深入，则回朔；

深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是： 
a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。 
b) 然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。 
c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。 
图示如下：

这里写图片描述

注：红色数字代表遍历的先后顺序，所以图(e)无向图的深度优先遍历的顶点访问序列为：V0，V1，V2，V5，V4，V6，V3，V7，V8 
如果采用邻接矩阵存储，则时间复杂度为O(n2)；当采用邻接表时时间复杂度为O(n+e)。 

//深度优先遍历----邻接矩阵方式  
typedef int Boolean;//Boolean 是布尔类型，其值是TRUE 或FALSE  
Boolean visited[MAX];//访问标志的数组  
//邻接矩阵的深度优先递归算法  
void DFS(MGraph G, int i)  
{  
    int j;  
    visited[i] = TRUE;  
    printf("%c", G.vexs[i]);  
    for (j = 0; j < G.numVertexes; j++)  
        if (G.arc[i][j] == 1 && !visited[j])  
            DFS(G, j);//对未访问的邻接顶点递归调用  
}  
//邻接矩阵的深度遍历操作  
void DFSTraverse(MGraph G)  
{  
    int i;  
    for (i = 0; i < G.numVertexes; i++)  
        visited[i] = FALSE；//设置初始所有顶点状态都是未访问状态  
        for (i = 0; i < G.numVertexes; i++)  
            if (!visited[i])//对未访问过的顶点调用DFS,若是连通图，只会执行一次???  
                DFS(G, i);  
}  
[cpp] view plain copy
//深度优先遍历----邻接表方式  
//邻接表的深度优先递归算法  
void DFS(GraphAdjList *GL, int i)  
{  
    EdgeNode *p;  
    visited[i] = TRUE;  
    printf("%c", GL->AdjList[i].data);//打印顶点，也可以其他操作  
    p = GL->adjListed[i].firstedge;  
    while (p)  
    {  
        if (!visited[p->adjvex])  
            DFS(GL, p->adjvex);//对未访问的邻接顶点递归调用  
        p = p->next;  
    }  
}  
//邻接表的深度遍历操作  
void DFSTraverse(GraphAdjList *GL)  
{  
    int i;  
    for (i = 0; i < GL->numVertexes; i++)  
        visited[i] = FALSE;  
    for (i = 0; i < G.numVertexes; i++)  
        if (!visited[i])//对未访问过的顶点调用DFS,若是连通图，只会执行一次  
            DFS(GL, i);  
}

BFS  广度优先搜索遍历 


广度优先搜索遍历BFS类似于树的按层次遍历。

其基本思路是： 

a) 首先访问出发点Vi 
b) 接着依次访问Vi的所有未被访问过的邻接点Vi1，Vi2，Vi3，…，Vit并均标记为已访问过。 
c) 然后再按照Vi1，Vi2，… ，Vit的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。 
图示如下： 

 

如果采用邻接矩阵存储，则时间复杂度为O(n2)，若采用邻接表，则时间复杂度为O(n+e)。 
//广度优先遍历----邻接矩阵方式  
void BFSTraverse(MGraph G)  
{  
    int i, j;  
    Queue Q;  
    for (i = 0; i < G.numVertexes; i++)  
        visited[i] = FALSE;  
    InitQueue(&Q);//初始化一个辅助用的队列  
    for（i = 0; i < G.numVertexes; i++)//对每个顶点做循环  
    {  
    if (!visited[i])//若顶点i未被访问过就做以下处理  
    {  
        visited[i] = TRUE;//设置当前顶点访问过  
        printf("%c", G.vexs[i]);  
        EnQueue(&Q,i);//将此顶点入队列  
        while (!QueueEmpty(Q))  
        {  
            DeQueue(&Q, &i);//将队中元素出列，并赋值给i  
            for (j = 0; j < G.numVertexes; j++)  
            {  
                //判断其他顶点与当前顶点之间是否存在边且未访问过  
                if (G.arc[i][j] == 1 && !visited[j])  
                    visited[j] = TRUE;  
                printf("%c", G.vexs[j]);  
                EnQueue(&Q, j);//出队入队操作主要是为了获得上一个顶点的序号  
            }  
        }  
      }  
    }  
}  
//广度优先遍历----邻接表方式  
void BFSTraverse(GraphAdjList GL)  
{  
    int i;  
    EdgeNode *p;  
    Queue Q;  
    for (i = 0; i < GL->numVertexes; i++)  
        visited[i] = FALSE;  
    InitQueue（&Q);  //初始化队列
    for（i = 0; i < G->numVertexes; i++)//对每个顶点做循环  
    {  
    if (!visited[i])//若顶点i未被访问过就做以下处理  
    {  
        visited[i] = TRUE;//设置当前顶点访问过  
        printf("%c", G->AdjList[i].data);  
        EnQueue(&Q,i);//将此顶点入队列  
        while (!QueueEmpty(Q))  
        {  
            DeQueue(&Q, &i);//将队中元素出列，并赋值给i  
            p = GL->AdjList[i].firstedge;//找到当前顶点边表链表头指针  
            while (p)  
            {  
                if (!visited[p->adjvex])  
                {  
                    visited[p->adjvex] = TRUE;  
                    printf("%c", GL->adjList[p->adjvex].data);  
                    EnQueue(&Q, p->adjvex);  
                }  
                p = p->next;//指针指向下一个邻接点  
            }  
        }  
    }  
   }  
}

最小生成树

即构造连通网的最小代价生成树 

有两种经典算法计算一个图的最小生成树：Prim算法、Kruskal算法

1、prim算法

（存储结构---邻接矩阵）、（适用于边数较多时）

  时间复杂度O（n2）

思想：从连通网N={V,E}中的某一顶点U0出发，选择与它关联的具有最小权值的边(U0,v)，将其顶点加入到生成树的顶点集合U中。以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u,v),把它的顶点加入到集合U中。如此继续下去，直到网中的所有顶点都加入到生成树顶点集合U中为止。

具体过程

图中（g）、（h）都是最小生成树

//prim 算法生成最小生成树
	void MiniSpanTree_Prim(MGraph G)
	{
		int min, i, j, k;
		int adjvex[MAXVEX];//保存相关顶点下标
		int lowcost[MAXVEX];//保存相关顶点间边的权值
		lowcost[0] = 0;//初始化第一个顶点为零，即v0加入生成树。
		//lowcost[0]=0表示v0已经被纳入最小生成树中,之后凡是lowcost数组中的值被设置为0就是表示此下标的顶点被纳入最小生成树
		adjvex[0] = 0;//初始化第一个顶点下标为0，即现在从v0开始（从哪儿开始无关紧要）
		for (i = 1; i < G.numVertexes; i++)//读取邻接矩阵第一行数据，循环除下标为0外的全部顶点
		{
			lowcost[i] = G.arc[0][i];//将v0顶点与之有边的权值存入数组
			adjvex[i] = 0;//初始化都为v0的下标
		}
		for（i = 1; i < G.numVertexes; i++)//构造最小生成树
	{
	min = INFINITY;//初始化最小权值为无穷
	j = 1; k = 0;
	while (j < G.numVertexes)//循环全部顶点
	{
		if（lowcost[j] != 0 && lowcost[j] < min)//如果权值不为0且权值小于min
		{//lowcost[j] != 0的判断同时避免了回路的形成
		min = lowcost[j];//则让当前权值成为最小值
		k = j;//将当前最小值的下标存入k
		}
		j++;
	}
	printf("%d,%d", adjvex[k], k);//打印当前顶点边中权值最小边
	lowcost[k] = 0;//将当前顶点的权值设置为0，表示此顶点已经完成任务
	for (j = 1; j < G.numVertexes; j++)//通过此循环初始化邻接矩阵剩余行
	{
		if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
		{
			//若下标为k的顶点各边权值小于此前这些顶点未被加入生成树的权值 
			lowcost[j] = G.arc[k][j];//将较小权值存入lowcost
			adjvex[j] = k;//将下标为k的顶点存入adjvex
		}
	}
  }
}

2、KrusKal算法 

（存储结构--边集数组）、（适用于边数较少时）

  时间复杂度O（eloge）

 思想： Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。如果某条边的加入使图中形成了回路，则舍弃这条边


//Kruskal算法生成最小生成树
	//对边集数组Edge结构的定义
	typedef struct
	{
		int begin;
		int end;
		int weight;
	}Edge;
	void MiniSpanTree_Kruskal(MGraph G)//生成最小生成树
	{
		int i, n, m;
		Edge edges[MAXEDGE];//定义边集数组
		int parent[MAXVEX];//定义一个数组来判断边与边是否形成一个环路
	//此处省略将邻接矩阵G转化为边集数组edges并按权值由小到大排序的代码
		for (i = 0; i < G.numVertexes; i++)
			parents[i] = 0;//初始化数组值为0
		for (i = 0; i < G.numEdges; i++)//循环每一条边
		{
			n = Find(parent, edges[i].begin);
			m = Find(parent, edges[i].end);
			if (n != m)//如果n与m不等，说明此边没有与现有生成树形成环路
			{
				parent[n] = m;//将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中
				printf("%d,%d,%d", edges[i].begin, edges[i].end, edges[i].weight);
			}
		}
	
	}
	int Find(int *parent, int f)//查找连线顶点的尾部下标
	{
		while (parent[f] > 0)
			f = parent[f];
		return f;
	}
最短路径

两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。


1、Dijkstra算法

（求单源点无负边最短路径）（所用数据结构--邻接矩阵）

  (1)   迪杰斯特拉(Dijkstra)算法按路径长度递增次序产生最短路径。先把V分成两组：

  • S：已求出最短路径的顶点的集合
  • V-S=T：尚未确定最短路径的顶点集合

        将T中顶点按最短路径递增的次序加入到S中，依据：可以证明V0到T中顶点Vk的最短路径，或是从V0到Vk的直接路径的权值或是从V0经S中顶点到Vk的路径权值之和（反证法可证，说实话，真不明白哦）。

    (2)   求最短路径步骤

  1. 初使时令 S={V0},T={其余顶点}，T中顶点对应的距离值， 若存在<V0,Vi>，为<V0,Vi>弧上的权值（和ＳＰＦＡ初始化方式不同），若不存在<V0,Vi>，为Inf。
  2. 从T中选取一个其距离值为最小的顶点W(贪心体现在此处)，加入S(注意不是直接从S集合中选取，理解这个对于理解vis数组的作用至关重要)，对T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值比不加W的路径要短，则修改此距离值（上面两个并列for循环，使用最小点更新）。
  3. 重复上述步骤，直到S中包含所有顶点，即S=V为止（说明最外层是除起点外的遍历）。
  4. //Dijkstra算法求最短路径--求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v]
//P[v]的值为前驱顶点下标，D[v]表示v0到v的最短路径长度和
//调用此函数前，需要写出图的邻接矩阵，并定义参数v0为0
#define MAXVEX 9
#define INFINITY 65535
	typedef int Patharc[MAXVEX];//用于存储最短路径下标的数组
	typedef int ShortPathTable[MAXVEX];//用于存储到各点最短路径的权值和
	void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *p, ShortPathTable *D)
	{
		int v, w, k, min;
		int final[MAXVEX];//表示求得顶点v0至vW的最短路径
		for (v = 0; v < G.numVertexes; v++)//初始化数据
		{
			final[v] = 0;//全部顶点初始化为未知最短路径状态
			（*D）[v] = G.arc[v0][v];//将与v0点有连线的顶点加上权值
			（*P)[v] = 0;//初始化路径数组P为0
		}D数组为{65535,1,5,65535,65535,65535,65535,65535,65535}
		（*D)[v0] = 0;//v0至v0路径为0
		final[v0] = 1;//v0至v0不需要求路径    此时fina数组{1,0,0,0,0,0,0,0,0}
//开始主循环，每次求得v0到某个v顶点的最短路径
		for (v = 1; v < G.numVertexes; v++)//寻找离v0最近的顶点
		{
			min = INFINITY;
			for (w = 0; w < G.numVertexes; v++)
			{
				if (!final[w] && (*D)[w] < min)  //！final[w]表示如果v0到vw的最近距离还未求得
				{
					k = w;   //k=1
					min = (*D)[w];//w顶点离v0顶点更近    min=1
				}
			}
			final[k] = 1; //由k=1,表示与v0最近的顶点是v1,并且由D[1]=1,知道此时v0到v1的最短距离是1，final{1,1,0,0,0,0,0,0,0}
			for (w = 0; w < G.numVertexes; w++)//修正当前最短路径及距离

			{
				//如果经过v顶点的路径比现在这条路径的长度短的话
				if(!final[w]&&(min+G.arc[k][w]<(*D)[w]))
				{//说明找到了更短的路径，修改D[w]和P[w]
					(*D)[w] = min + G.arc[k][w];
					(*p)[w] = k;
			     }
		   }
}
      时间复杂度O(n^2)

       其实根据最终返回的数组D和数组P，是可以得到V0到任意一个顶点的最短路径和路径长度。

最后P数组为{0,0,1,4,2,4,3,6,7}

P[8]=7表示v0到v8的最短路径，顶点v8的前驱是v7,再由P[7]=6表示v7的前驱是v6,P[6]=3,表示v6的前驱是v3..........

得到v0到v8的最短路径为v8<----v7<---v6<---v3<----v4<----v2<------v1<----v0

2、 Floyd算法

（求所有顶点到所有顶点的最短路径）

   

 Floyd算法的基本思想如下：从任意节点A到任意节点B的最短路径不外乎2种可能，

1是直接从A到B

2是从A经过若干个节点到B

所以，我们假设dist(AB)为节点A到节点B的最短路径的距离，对于每一个节点K，我们检查dist(AK) + dist(KB) < dist(AB)是否成立，如果成立，证明从A到K再到B的路径比A直接到B的路径短，我们便设置 dist(AB) = dist(AK) + dist(KB)，这样一来，当我们遍历完所有节点K，dist(AB)中记录的便是A到B的最短路径的距离。

首先准备两个矩阵D-1和P-1, D-1就是网图的邻接矩阵，P-1初设为P[i][j]=j这样的矩阵，主要用来存储路径。准备工作即代码中的初始化过程


//Floyd算法求最短路径--求各顶点v到其余顶点w最短路径P[v][w]及带权长度D[v][w]
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
void ShorttestPath_Floyd(MGraph G, Pathmatirx *P, ShortPathTable *D)
{
	int v, w, k;
	for (v = 0; v < G.numVertexes; ++v)//初始化D与P
	{
		for (w = 0; w < G.numVertexes; ++w)
		{
			(*D)[v][w] = G.matrix[v][w];//D[v][w]值即为对应点间的权值
			（*p)[v][w] = w;//初始化P
		}
	}
	for (k = 0; k < G.numVertexes; ++k);//k=0即所有顶点都经过v0中转，v代表起始顶点,w代表结束顶点
	{
		for (v = 0; v < G.numVertexes; ++v)
		{
			for (w = 0; w < G.numVertexes; ++w)
			{
				if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w])
				{
					//如果经过下标k的顶点路径比原两点间路径短
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w]；
					（*p)[v][w] = (*p)[v][k];//路径设置为下标为k的顶点
				}
			}
		}
	}
}
时间复杂度O(n^3)
最后得到的D与P的矩阵

如何由P这个路径数组得出具体的最短路径？以v0到v8为例，从右图的第v8列，P[0][8]=1，得到要经过顶点v1,然后将1取代0得到P[1][8]=2,说明要经过v2,然后将2取代1得到P[2][8]=4，说明要经过v4............................

最后得出最短路径为v0->v1->v2->v4->v3->v6->v7->v8

/*求最短路径的显示代码*/
for（v = 0; v < G.numVertexes; ++v)
	{
	for (w = v + 1; w < G.numVertexes; w++)
	{
		printf("v%d-v%d weight: %d", v, w, D[v][w]);
		k = P[v][w];//获得第一个路径顶点下标
		printf(" path:%d", v);//打印源点
		while（k != w)
		{
		printf("-> %d", k);//打印路径顶点
		k = P[k][w];//获得下一个路径顶点下标
     }
		printf（"-> %d\n", w);//打印终点
	}
	printf("\n");
}

 当要求所有顶点至所有顶点的最短路径时，可以选择弗洛伊德算法，虽然其复杂度有点高。






practicePLUS
关注
专栏目录
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值