游戏开发中的数学问题:技能伤害的区域检测(方形,圆形,三角形,扇形)

众所周知,moba中的每个英雄都有一套自己的技能的攻击范围方式，有如廉颇一样的圆形范围，有火舞一样的直线范围，吕布的扇形方天戟范围，还有牛魔大招时的矩形范围等等
一些技能是通过物理的碰撞检测来判断的，物理检测的诟病就在于开销过大,一般的,不会在游戏中使用物理碰撞来实现范围伤害.那么用什么呢?
大多数是通过范围来检测的。所以在能考虑不用物理来检测的情况下,开发者更倾向来自己通过算法模拟实现.

此篇和各位一起研究一下几种范围伤害的判断.

矩形范围判断

不管技能的特效有多炫酷,在背后都是规规矩矩的范围判断.矩形是范围判断中最简单的一种.首先,只要知道对角的两个点,就可以判断出敌人是否是在这个矩形范围内了.为什么呢?因为在游戏开发过程中,技能一般是在地面上的,那么.就确定这两个点是在这个平面上.然后对角的两个点可以把另一个对角的点确定出来.
首先,我们通过2个已知的点确定一个矩形,我们需要一个Rectangle的类,用来获取4个点和判断某个点是否在矩形内.

首先是通过2个已知点得出其他的两个点:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class Rectangle
 6{
 7
 8    public Vector3 corner1;//四边形的一个对角位置
 9    public Vector3 corner2;//四边形的另一个对角位置
10
11    //获得四个角顶点
12    public void GetVerts(out Vector3 vertex0, out Vector3 vertex1, out Vector3 vertex2, out Vector3 vertex3)
13    {
14        vertex0 = this.corner1;
15        vertex1 = new Vector3(this.corner2.x, 0, this.corner1.z);
16        vertex2 = this.corner2;
17        vertex3 = new Vector3(this.corner1.x, 0, this.corner2.z);
18    }
19}

我们就通过这个方法,获得矩形的4个点,来画出矩形的区域:

1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class TestRt : MonoBehaviour
 6{
 7
 8    //public Transform Point;
 9    public Transform RtPoint0, RtPoint1;
10    public Rectangle rtBox;
11
12    private const float _pointRadius = 0.1f;
13
14    private void OnDrawGizmos()
15    {
16        rtBox = CreateFromTwoPoints(RtPoint0.position, RtPoint1.position);
17
18        if (rtBox != null)
19        {
20            DrawFrameLine(rtBox); 
21        }
22    }
23
24    public Rectangle CreateFromTwoPoints(Vector3 point0, Vector3 point1)
25    {
26        Rectangle rt = new Rectangle();
27        if (point0.x < point1.x)
28        {
29            rt.corner1.x = point0.x;
30            rt.corner2.x = point1.x;
31        }
32        else
33        {
34            rt.corner1.x = point1.x;
35            rt.corner2.x = point0.x;
36        }
37        if (point0.z < point1.z)
38        {
39            rt.corner1.z = point0.z;
40            rt.corner2.z = point1.z;
41        }
42        else
43        {
44            rt.corner1.z = point1.z;
45            rt.corner2.z = point0.z;
46        }
47        return rt;
48    }
49
50    protected void DrawFrameLine(Rectangle box)
51    {
52        Vector3 v0, v1, v2, v3;
53        box.GetVerts(out v0, out v1, out v2, out v3);  
54        Gizmos.DrawLine(v0, v1);
55        Gizmos.DrawLine(v1, v2);
56        Gizmos.DrawLine(v2, v3);
57        Gizmos.DrawLine(v3, v0);
58    }
59}

然后对2个点进行赋值,注意,Y轴要为0,因为我们规定的平面是xz平面.那么我们看看画出的效果:

判断就更为简单了,同样的这个点的Y轴要为0.我们做个这样的功能,当这个点在矩形范围内的时候,框变红,如果不在,框为蓝色:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class TestRt : MonoBehaviour
 6{
 7
 8    public Transform Point;
 9    public Transform RtPoint0, RtPoint1;
10    public Rectangle rtBox;
11
12    private const float _pointRadius = 0.1f;
13
14    private void OnDrawGizmos()
15    {
16        rtBox = CreateFromTwoPoints(RtPoint0.position, RtPoint1.position);
17        bool cont = rtBox.CheckisInzone(Point.position);
18        if (cont)
19        {
20            Gizmos.color = Color.red; 
21        }
22        else
23        {
24            Gizmos.color = Color.blue; 
25        }
26
27        if (rtBox != null)
28        {
29            DrawFrameLine(rtBox);
30            Gizmos.DrawSphere(Point.position, _pointRadius);
31        }
32    }
33
34    public Rectangle CreateFromTwoPoints(Vector3 point0, Vector3 point1)
35    {
36        Rectangle rt = new Rectangle();
37        if (point0.x < point1.x)
38        {
39            rt.corner1.x = point0.x;
40            rt.corner2.x = point1.x;
41        }
42        else
43        {
44            rt.corner1.x = point1.x;
45            rt.corner2.x = point0.x;
46        }
47        if (point0.z < point1.z)
48        {
49            rt.corner1.z = point0.z;
50            rt.corner2.z = point1.z;
51        }
52        else
53        {
54            rt.corner1.z = point1.z;
55            rt.corner2.z = point0.z;
56        }
57        return rt;
58    }
59
60    protected void DrawFrameLine(Rectangle box)
61    {
62        Vector3 v0, v1, v2, v3;
63        box.GetVerts(out v0, out v1, out v2, out v3);  
64        Gizmos.DrawLine(v0, v1);
65        Gizmos.DrawLine(v1, v2);
66        Gizmos.DrawLine(v2, v3);
67        Gizmos.DrawLine(v3, v0);
68    }
69}

我们来看下效果:

不在矩形范围内:

在矩形范围内:
在这里插入图片描述

总结:矩形不一定是通过两个对角的点来确定.也可以通过一个中间点,然后对于中间点,偏移某个变量.也可以生成一个矩形的判断范围,只要知道四个角的点位置,就能判断.

圆形范围判断

圆形的范围判断似乎也很简单.首先确保点都在同一个平面上,知道圆形的中心点以及半径的大小,判断某个点与圆心的距离,如果小于半径,那么就是在圆里,反之,就在圆外.
那么,真的可以这么简单的实现出来吗?
我们首先定义圆心以及半径的大小.绘制一个圆形,因为unity中没有绘制曲线的接口,所以我们打算用若干个点组成一个近似的圆形.其实本质上是个多边形.

首先我们要明白,只知道圆心和半径,怎么找出若干个点.围成一个近似圆的图形.那么,这里有个概念要清楚:弧度.弧度是干什么的呢?抛去复杂的解释,简单的来说就是单位圆的周长为2π , 2π 的弧度代表一个完整的圆. 记作: 2 πrad 一个圆的度数是360度,那么一个弧度就是180/π 那么也许你会有疑问,知道弧度能干啥呢?我们可以这样.假设我们的近似圆的多边形为正50边形,那么我们就可以通过弧度来计算出角度 :2π /50 即可等于单个的角度
有点像这种感觉:
那么通过弧度,就可以计算出点的位置了,公式如下:

其中center为圆心,radius为半径,randian为弧度.

好的,那么我们运用公式,写出绘制点的方法:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class circleTest : MonoBehaviour
 6{
 7    //圆心
 8    public Transform Center;
 9    //半径
10    public float Radius;
11    //多边形精度
12    public int count = 40;
13    private void OnDrawGizmos()
14    { 
15        DrawCircle(); 
16    }
17
18    protected void DrawCircle()
19    {
20        Gizmos.color = Color.blue;
21        float radian = 2f * Mathf.PI / count;
22        //绘制圆形基础点的个数 适当即可
23        //Vector3 prev = Getposition(0);
24        for (int i = 1; i <= count; ++i)
25        {
26            Vector3 curr = new Vector3(
27                Center.position.x + (Radius * Mathf.Cos(i * radian)),
28                0,
29                Center.position.z + (Radius * Mathf.Sin(i * radian)));
30
31            Gizmos.DrawSphere(curr, 0.05f);
32
33        }
34    } 
35}

那么,我们可以看到一个近似圆的点的集合:

那么.我们和之前一样,如果目标点在园内,就是红色,如果不在,那就是蓝色.我们在原有代码基础上修改:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class circleTest : MonoBehaviour
 6{
 7    public Transform Point;
 8    //圆心
 9    public Transform Center;
10    //半径
11    public float Radius;
12    //多边形精度
13    public int count = 40;
14    private void OnDrawGizmos()
15    { 
16        DrawCircle(); 
17    }
18
19    protected void DrawCircle()
20    {
21        if (checkInZone(Point.position))
22        {
23            Gizmos.color = Color.red;
24        }
25        else
26        {
27            Gizmos.color = Color.blue;
28        }
29      ...
30    }
31
32    bool checkInZone(Vector3 pointPos)
33    {
34        Vector3 offset = pointPos - Center.position;
35        if (offset.sqrMagnitude <= (Radius * Radius))
36        {
37            return true;
38        }
39        return false;
40    }
41}

那么进行一个测试:

检测点在圆的外部:

检测点在圆的内部

三角形范围判断

三角形呢,其实是一个比较复杂的判断,绘制图像倒还好说,就是三个点,直接就可以绘制出来一个三角形,不过为了将问题简单化,所以还是老样子,我们的三角形三个点的Y轴都是0.

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class Triangle : MonoBehaviour
 6{
 7    public Transform pos1;
 8    public Transform pos2;
 9    public Transform pos3;
10
11    private void OnDrawGizmos()
12    {
13        Gizmos.DrawLine(pos1.position, pos2.position);
14        Gizmos.DrawLine(pos2.position, pos3.position);
15        Gizmos.DrawLine(pos3.position, pos1.position);
16    }
17}

太简单了,就不放图片了.反正各位都能看出来
好的,接下来就要说到比较复杂的东西了,其实讲出来也不算复杂,只是初中的知识.判断一个点是否在三角形内,大概有3种办法
第一种办法:内角和法

在这里插入图片描述

连接P点和三角形的三个顶点,得到三条线段PA,PB和PC,求出这三条线段与三角形各边的夹角,如果所有的夹角的内角和为180,那么就说明P点在三角形内,否则,就不在.但是这种办法如果是几何题,那么很好解,但是在我们的程序中,这个不好实现,因为需要加6个角,然后各种向量的计算.所以一般的,这种耗费性能的操作,直接舍弃掉.
第二种办法:同向法

那么同向法怎么理解呢?就是不管你是顺时针还是逆时针去遍历这些线段,会发现P点始终在这条线的一侧,如果是顺时针,那么线段就是AB ,BC ,CA ,会发现P点始终就是在你的右侧. 如果不符合这个规律,那么这个点就不在三角形内.
第三种方法重心法

三角形上的点都有这样的一个特性,假如B点,假设是A点移动了AB的一段距离,C点就是A移动了AC距离, 其中UV的取值范围为正,且U+V<1.

我们这里直接使用重心法

 1using UnityEngine;
 2
 3public class Triangle :MonoBehaviour
 4{
 5
 6    public Transform V1, V2, V3, Point;
 7
 8    private void OnDrawGizmos()
 9    {
10        bool isInangle = IsPointInTriangle(V1.position , V2.position , V3.position , Point.position ); 
11        if (isInangle)
12        {
13            Gizmos.color = Color.red;
14        }
15        else
16        {
17            Gizmos.color = Color.blue;
18        }
19        Gizmos.DrawLine(V1.position , V2.position );
20        Gizmos.DrawLine(V2.position , V3.position );
21        Gizmos.DrawLine(V3.position , V1.position );
22    }
23
24
25
26    bool IsPointInTriangle(Vector3 p1, Vector3 p2, Vector3 p3, Vector3 targetPoint)
27    {
28        Vector3 v0 = p2 - p1;
29        Vector3 v1 = p3 - p1;
30        Vector3 v2 = targetPoint - p1;
31
32        float _00 = Vector3.Dot(v0, v0);
33        float _01 = Vector3.Dot(v0, v1);
34        float _02 = Vector3.Dot(v0, v2);
35        float _11 = Vector3.Dot(v1, v1);
36        float _12 = Vector3.Dot(v1, v2);
37
38        float inver = 1 / (_00 * _11 - _01 * _01);
39        float u = (_11 * _02 - _01 * _12) * inver;
40        if (u < 0 || u > 1)
41            return false;
42        float v = (_00 * _12 - _01 * _02) * inver;
43        if (v < 0 || v > 1)
44            return false;
45        return u + v < 1;
46    }
47}

我们来试试效果:当点在三角形内:

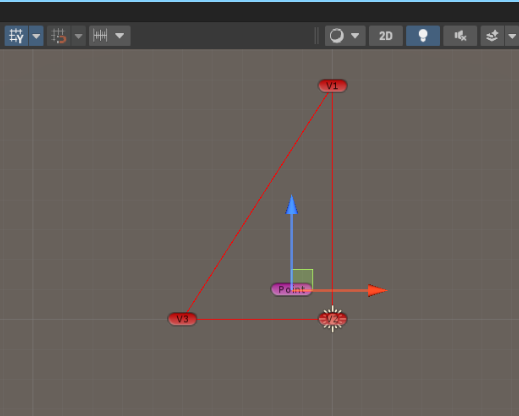
当点不在三角形内:

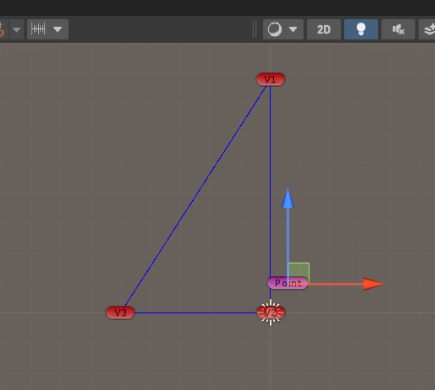
扇形范围判断

扇形范围判断,其实我们可以理解为一个圆形的判断变种,只是在特定的圆形角度里面才会判断,如果不在这个角度中,直接返回一个false即可.

首先还是先画出一个扇形,我们这样来设计,比如这个扇形的角度是60度,我们分为左右,一边30度,这样对于程序好写一点,首先画出扇形的两个边:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class Fanshaped : MonoBehaviour
 6{
 7    public float angel = 60;
 8    public float radius = 4;
 9
10
11    private void OnDrawGizmos()
12    {
13        //
14        float x = radius * Mathf.Sin(angel / 2 * Mathf.Deg2Rad);//角度转换为弧度
15        float y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
16        Vector3 a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
17        Vector3 b = new Vector3(transform.position.x + x, 0, transform.position.z + y);
18
19        Gizmos.DrawLine(transform.position, a);
20        Gizmos.DrawLine(transform.position, b);
21
22
23
24    }
25}

然后就是和圆形差不多的算法,绘制一个弧形:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class Fanshaped : MonoBehaviour
 6{
 7    public float angel = 60;
 8    public float radius = 4;
 9    public int count = 10;//扇形的精度
10
11    private void OnDrawGizmos()
12    {
13        //
14        float x = radius * Mathf.Sin(angel / 2 * Mathf.Deg2Rad);//角度转换为弧度
15        float y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
16        Vector3 a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
17        Vector3 b = new Vector3(transform.position.x + x, 0, transform.position.z + y);
18
19        Gizmos.DrawLine(transform.position, a);
20        Gizmos.DrawLine(transform.position, b);
21
22        float half = angel / 2;
23
24        for (int i = 0; i <= count ; i++)
25        {  
26
27            float temp = (half / count);
28            temp *= i; 
29            x = radius * Mathf.Sin((temp) * Mathf.Deg2Rad);
30            y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
31            a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
32            Gizmos.DrawSphere(a, 0.05f);
33            x = radius * Mathf.Sin((-temp) * Mathf.Deg2Rad);
34            y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
35            a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
36            Gizmos.DrawSphere(a, 0.05f);
37        }
38
39    }
40}

绘制的弧形如下:

![在这里插入图片描述](https://img-blog.csdnimg.cn/197b8c63e2b74198a52c2f8ec6335ae1.png

下面我们开始判断点是否在扇形内:

 1using System.Collections;
 2using System.Collections.Generic;
 3using UnityEngine;
 4
 5public class Fanshaped : MonoBehaviour
 6{
 7    public Transform Point;
 8
 9    public float angel = 60;
10    public float radius = 4;
11    public int count = 10;//扇形的精度
12
13    private void OnDrawGizmos()
14    {
15        //
16        float x = radius * Mathf.Sin(angel / 2 * Mathf.Deg2Rad);//角度转换为弧度
17        float y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
18        Vector3 a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
19        Vector3 b = new Vector3(transform.position.x + x, 0, transform.position.z + y);
20
21        Gizmos.DrawLine(transform.position, a);
22        Gizmos.DrawLine(transform.position, b);
23
24        float half = angel / 2;
25
26        if (IsInRange(Point))
27        {
28            Gizmos.color = Color.red;
29        }
30        else
31        {
32            Gizmos.color = Color.blue;
33        }
34
35        for (int i = 0; i <= count ; i++)
36        {  
37
38            float temp = (half / count);
39            temp *= i; 
40            x = radius * Mathf.Sin((temp) * Mathf.Deg2Rad);
41            y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
42            a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
43            Gizmos.DrawSphere(a, 0.05f);
44            x = radius * Mathf.Sin((-temp) * Mathf.Deg2Rad);
45            y = Mathf.Sqrt(Mathf.Pow(radius, 2) - Mathf.Pow(x, 2f));
46            a = new Vector3(transform.position.x - x, 0, transform.position.z + y);
47            Gizmos.DrawSphere(a, 0.05f);
48        }
49
50    }
51
52
53    public bool IsInRange( Transform target)
54    {
55        //攻击者位置指向目标位置的向量
56        Vector3 direction = target.position - transform.position;
57        //点乘积结果
58        float dot = Vector3.Dot(direction.normalized, transform.forward);
59        //反余弦计算角度
60        float offsetAngle = Mathf.Acos(dot) * Mathf.Rad2Deg;
61        return offsetAngle < angel  * .5f && direction.magnitude < radius ;
62    }
63}

我们像之前一样的去测试一下.
如果点在扇形内:

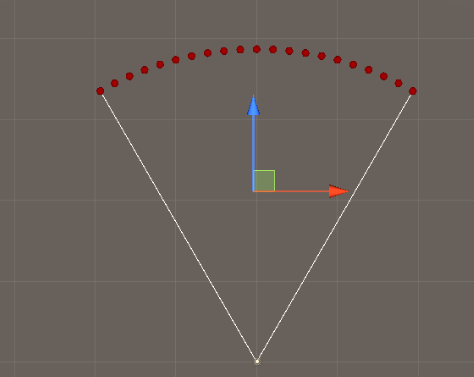
如果不在:![在这里插入图片描述](https://img-blog.csdnimg.cn/61d5dfe386af42479b47f9b2eb56e666.png

引申
那么如果是扇形的环呢?其实,我们只需要判断点到圆心的距离,是否是在环内就可以了.