正态分布

最新推荐文章于 2022-08-01 21:53:50 发布

二六

最新推荐文章于 2022-08-01 21:53:50 发布

阅读量1k

点赞数

分类专栏：概率统计文章标签：概率统计

本文链接：https://blog.csdn.net/weixin_41692282/article/details/92790455

版权

6 篇文章

订阅专栏

概率密度函数可用于描述连续数据。通过它可以求出一个数据范围内的某个连续变量的概率。

概率密度通过面积标示概率大小。

从图中直接读出概率数值仅适用于离散概率的求解。

处理连续数据时，所计算的是一个数值范围的概率。

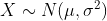
正态（Normal）分布又叫高斯分布，它是连续型概率分布。

通过 $\mu$ 和 $\sigma ^{2}$ 进行定义。 $\mu$ 指出曲线的中央位置， $\sigma$ 指出分散性。

以上是X~N(0,1),X~N(0,2),X~N(0,4)的正态分布图，可以看出当 $\sigma ^{2}$ 越大，正态分布曲线越扁平、越宽。

以上是X~N(0,1)，X~N(1,1)的正态分布图，可以看出 $\mu$ 指出中央位置。

正态概率计算方法步骤：

1.确定分布与范围。 $X\sim N(\mu ,\sigma ^{2})$

2.标准化。 $X\sim N(\mu ,\sigma ^{2})\rightarrow Z\sim N(0,1)$

Z=(X- $\mu$ )/ $\sigma$ .

3.查找标准正态分布概率表

情况	分布	条件
X+Y $X\sim N(\mu_{x} ,\sigma_{x}^{2}),Y\sim N(\mu_{y} ,\sigma_{y}^{2})$	$X+Y\sim N(\mu_{x}+\mu_{y},\sigma_{x} ^{2}+\sigma_{y} ^{2})$	X与Y为独立变量
X-Y $X\sim N(\mu_{x} ,\sigma_{x}^{2}),Y\sim N(\mu_{y} ,\sigma_{y}^{2})$	$X-Y\sim N(\mu_{x}-\mu_{y},\sigma_{x} ^{2}+\sigma_{y} ^{2})$	X与Y为独立变量
aX+b $X\sim N(\mu ,\sigma ^{2})$	$aX+b\sim N(a\mu+b ,a^{2}\sigma ^{2})$	a,b为常量
X1+X2+……Xn $X\sim N(\mu ,\sigma ^{2})$	$X_{1}+X_{2}+\cdots +X_{n}\sim N(n\mu ,n\sigma ^{2})$	X1,X2,……Xn为X的独立观察结果
X的正态近似 X~B(n,p)	$X\sim N(np,npq)$	np>5,nq>5,需要连续性修正
X的正态近似 X~Po( $\lambda$ )	X~N( $\lambda$ , $\lambda$ )	$\lambda$ >15, 需要连续性修正