基于图
我们的目的是将整张图量化为一个特征，这里传统的做法是利用 Graph Kernel 来衡量两个图的相似度。
图中的Kernel我们进行如下的定义：
Kernel K ( G , G ′ ) ∈ R K\left(G, G^{\prime}\right) \in \mathbb{R} K(G,G′)∈R 衡量数据之间的相似性。存在一个特征表示 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) such ，使得 K ( G , G ′ ) = ϕ ( G ) T ϕ ( G ′ ) K\left(G, G^{\prime}\right)=\phi(G)^{\mathrm{T}} \phi\left(G^{\prime}\right) K(G,G′)=ϕ(G)Tϕ(G′)。
Kernel 方法在图结构中的研究主要有两类：一是 Graph embedding 算法，将图(Graph)结构嵌入到向量空间；另一类就是 Graph kernel 算法。
第一类得到图结构的向量化表示，然后直接应用基于向量的核函数(RBF kernel, Sigmoid kernel, etc.) 处理，但是这类方法将结构化数据降维到向量空间损失了大量结构化信息。而 Graph kernel 直接面向图结构数据，既保留了核函数计算高效的优点，又包含了图数据在希尔伯特高维空间的结构化信息。
其中包括：
- Graphlet Kernel
- Weisfeiler Lehman Kernel
- Random walk kernel
- Shortest path graph kernel
- …
我们将着重学习前两个Kernel。
a. Graphlet Kernel
在前面基于节点的方法中，其实已经介绍过Graphlet系列方法，总体思想还是一样的，我们需要构造一个类似“词袋”模型的向量，但与节点层面的Graphlet不同，图层面的Graphlet考虑了单独的节点情况，同时不涉及root节点。
三个节点与四个节点构成所有可能的Graphlets如下：
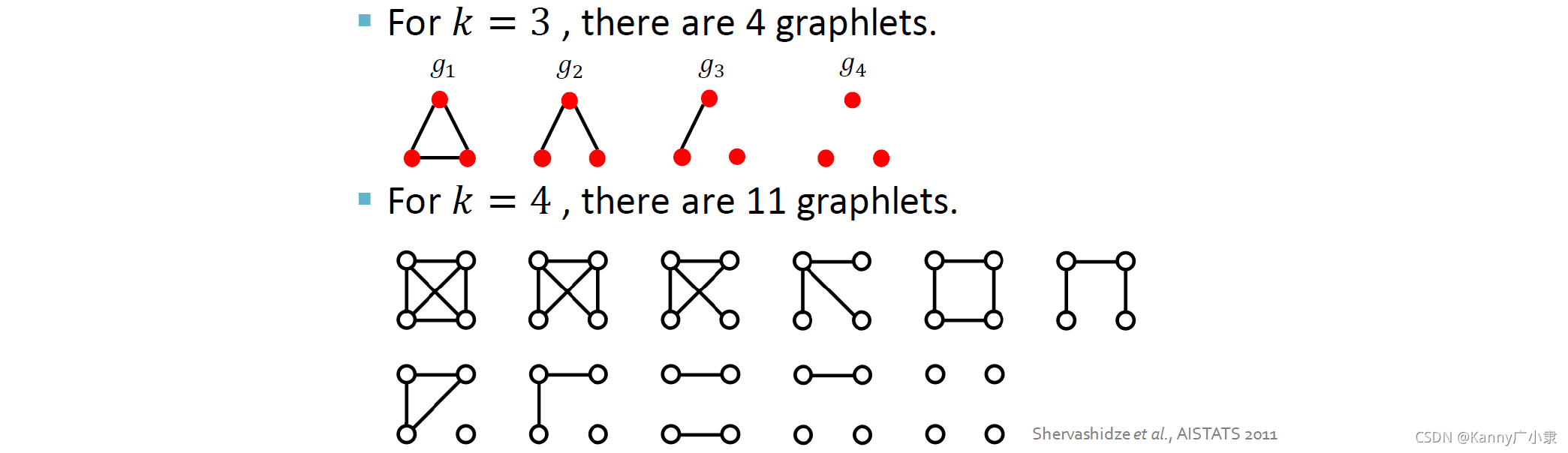
给定一个图 G G G与一个graphlet list G k = \mathcal{G}_{k}= Gk= ( g 1 , g 2 , … , g n k ) \left(g_{1,} g_{2}, \ldots, g_{n_{k}}\right) (g1,g
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
