目录
①高斯投影正算:大地坐标/经纬度坐标(L, B) ==> 平面坐标(X, Y)。
②高斯投影反算:平面坐标(X, Y) ==> 大地坐标/经纬度坐标(L, B)。
4.Environment and Configuration
1.Intro
搞了一段时间的WebGIS和接口,突然被领导喊来研究松散型切片(PNG)的切片方法,看到某人写的源码后傻眼了,东拼西凑导致最后瓦片拼接成图的时候,会造成偏差但又找不到原因,美名其曰研究,其实就是收拾烂摊子,水仙不开花装蒜呢。好在人帅功夫深(事实),发现是平面坐标转大地坐标/经纬度坐标(反算)的时候,椭球参数计算误差造成的精度丢失,最后大地坐标转瓦片坐标的时候,自然存在了偏移。
本着能Ctrl+CV绝不自己写的原则,提取了那一滩狗屎代码里的精华,又参考了网上的一些内容(就是copy),单独生成了一个能设置椭球参数和进行高斯正反算的模块。而关于椭球参数(这里指七参),最好找官方或者论文资料的数据,比较可信,有些文章代码里的七参精度存在一定误差。
这篇文章就总结一下椭球七参数计算和高斯投影生反算的一些公式和方法,高斯投影正反算理论比较晦涩,可能存在某些地方说不清楚或比较乱的,做个参考就ok。
2.Details
(1)椭球参数
| (参数/椭球名称) | CGCS 2000 | WGS 84 |
GRS 80
|
| 长半轴 a | 6378137 | 6378137 |
6378137
|
| 短半轴 b | 6356752.3141403558 | 6356752.3142451795 |
6356752.3141403474
|
| 极点子午圈曲率半径 c | 6399593.6258640232 | 6399593.6257584931 |
6399593.6258640316
|
| 椭球扁率 f | 0.0033528106811823 | 0.00335281066475 |
0.00335281068118
|
| 椭球扁率倒数 1/f |
298.257222101
|
298.257223563
| 298.2572221012063 |
| 第一偏心率 e1 | 0.0818191910428158 | 0.0818191908426215 |
0.0818191910428318
|
| 第二偏心率 e2 | 0.0820944381519172 | 0.0820944379496957 |
0.0820944381519334
|
| 椭球第一偏心率平方 e12 | 0.0066943800229008 | 0.0066943799901413 |
0.0066943800229034
|
| 椭球第二偏心率平方 e22 | 0.0067394967754790 | 0.0067394967422764 |
0.0067394967754816
|
椭球参数是参考椭球的几何参数,是高斯正反算和定义经度、纬度以及高程基础的重要依据,这里推荐一篇论文:2000国家大地坐标系椭球参数与GRS80和WGS84的比较_程鹏飞,里面只有三种椭球的参数,但是对于一般的生产和业务开发,CGCS2000和WGS84已经足够了。更多的椭球参数资料请看最后的下载链接。
(2)大地坐标、平面坐标
以下内容来自百度百科。
大地坐标:大地坐标(Geodetic coordinate)是大地测量中以参考椭球面为基准面的坐标,地面点P的位置用大地经度L、大地纬度B和大地高H表示。大地坐标多应用于大地测量学,测绘学等。而大地坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用大地经度、大地纬度和大地高度表示。大地坐标系的确立包括选择一个椭球、对椭球进行定位和确定大地起算数据。其实就是经纬度坐标。
平面坐标:表示点的平面位置。中国一般采用以高斯-克吕格投影分带的中央子午线为纵轴和赤道的投影为横轴的高斯-克吕格平面直角坐标系,简称高斯平面坐标系。坐标纵轴为x,自原点向北为正;坐标横轴为y,自原点向东为正。点的平面坐标为(x,y)。平面坐标系统是确定地面点平面位置所采用的参考系。大地测量、矿区控制测量、地形测量和工程测量所采用的平面坐标系主要有:高斯-克吕格平面直角坐标系、地方(矿区) 平面坐标系、独立坐标系。
3.Theory
(1)利用椭球长半轴和短半轴计算其它参数
已知椭球长半轴 a,短半轴b,求极点子午圈曲率半径 c、椭球扁率 f、椭球扁率倒数 1/f、第一偏心率 e1、第二偏心率 e2、椭球第一偏心率平方 e12、椭球第二偏心率平方 e22,并对应原始椭球参数表列出公式。
| (参数/结果) | CGCS 2000 | ***计算公式 |
输出结果(Python科学计算)
| 差值 |
| 长半轴 a | 6378137 | ———— |
————
| ———— |
| 短半轴 b | 6356752.3141403558 | ———— | ———— | ———— |
| 极点子午圈曲率半径 c | 6399593.6258640232 | 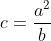 | 6399593.625864023 | 0.0000000002 |
| 椭球扁率 f | 0.0033528106811823 | 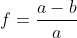 | 0.0033528106811822724 | 0.00000000000000003 |
| 椭球扁率倒数 1/f |
298.257222101
| 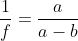 | 298.2572221010041 | 0.000000000004 |
| 第一偏心率 e1 | 0.0818191910428158 | 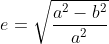 | 0.08181919104281517 | 0.0000000000000007 |
| 第二偏心率 e2 | 0.0820944381519172 | 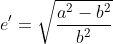 | 0.08209443815191658 | 0.0000000000000007 |
| 椭球第一偏心率平方 e12 | 0.0066943800229008 | 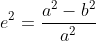 | 0.0066943800229006855 | 0.00000000000000012 |
| 椭球第二偏心率平方 e22 | 0.0067394967754790 | 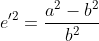 | 0.006739496775478857 | 0.00000000000000015 |
可以看到计算的参数结果和原始的参数结果误差小到可以忽略不计,这里就由取舍的小数位数来决定最后的误差大小,所以公式基本正确,以下为C#代码实现。
decimal a = 0.0M; // 椭球长半轴 a
decimal b = 0.0M; // 椭球短半轴 b
decimal c = pow(a, 2) / b; // 极点子午圈曲率半径 c
decimal e1 = sqrt(pow(a, 2) - pow(b, 2)) / a; // 第一偏心率 e1
decimal e2 = sqrt(pow(a, 2) - pow(b, 2)) / b; // 第二偏心率 e2
decimal e12 = pow(a, 2) - pow(b, 2) / pow(a, 2); // 椭球第一偏心率平方 e12
decimal e22 = pow(a, 2) - pow(b, 2) / pow(b, 2); // 椭球第二偏心率平方 e22
decimal f = (a - b) / a; // 椭球扁率 f
decimal f_ = a / (a - b); // 椭球扁率倒数 1/f 计算结果说明只需要知道长半轴 a 和短半轴 b 两个椭球参数值,就可以计算出其他的椭球参数。关于其他更多椭球参数表,之后会放到网盘上,提供下载链接(网上或者某个软件里找的)。
(2)高斯投影正反算

高斯投影正反算是大地坐标和平面坐标的相互转换方法。不过在查阅论文的时候,发现有论文提到高斯投影正反算也可以做大地坐标和高斯平面的直角坐标之间的转换。由于道行微末,就不做深究了,这里只涉及到大地坐标和平面坐标。
①高斯投影正算:大地坐标/经纬度坐标(L, B) ==> 平面坐标(X, Y)。
《大地测量学基础》高斯投影正反算章节中,发现可以用查表的方式进行简化。描述:在高斯投影坐标计算的实际工作中,往往采用查表和电算两种方式。为了便于查表计算,编有专门的计算用表,例如《高斯-克吕格投影计算表》(纬度0°~60°)。该表适用于高斯投影正算x,y精确至0.001m;高斯投影反算L,B精确至0.0001″。上表及其他有关用表都是对于克拉索夫斯基椭球而言的。公式简化如下:
其中,在编表时引用下列符号:
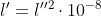
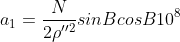
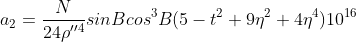
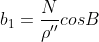
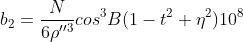
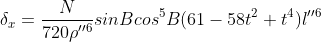
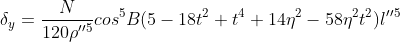
上式即为查表计算时的使用公式。式中 ,
,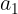 ,
,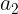 ,
,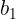 ,
,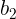 都可 以纬度为引数,
都可 以纬度为引数,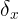 和
和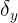 以
以 、
、 为引数,在该表中查取。其中
为引数,在该表中查取。其中  和
和 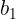 需要进行二次内插。
需要进行二次内插。
公式转换为代码,网上的大都大同小异,这里扒了一段作为代码实现,已经验证过了,转换结果基本正确。
实体代码:
/// <summary>
/// 高斯点实体
/// </summary>
public class GaussPoint
{
public GaussPoint()
{
}
/// <summary>
/// 高斯点实体
/// </summary>
/// <param name="x">平面坐标X</param>
/// <param name="y">平面坐标Y</param>
public GaussPoint(double x, double y)
{
this.X = x;
this.Y = y;
}
/// <summary>
/// 平面坐标X
/// </summary>
public double X { get; set; }
/// <summary>
/// 平面坐标Y
/// </summary>
public double Y { get; set; }
}高斯正算代码:
/// <summary>
/// 高斯正算方法(B, L) => (x, y)
/// </summary>
/// <param name="B">经度</param>
/// <param name="L">纬度</param>
/// <returns>高斯点实体</returns>
public GaussPoint GetXYFromBL(decimal B, decimal L)
{
decimal x = 0, y = 0;
// 计算临时值
decimal e4 = pow(e12, 2); // e2 * e2;
decimal e6 = pow(e12, 3); // e4 * e2;
decimal e8 = pow(e12, 4); // e6 * e2;
decimal e10 = pow(e12, 5); // e8 * e2;
decimal e_12 = pow(e12, 6); // e10 * e2;
decimal A1 = 1 + 3 * e12 / 4 + 45 * e4 / 64 + 175 * e6 / 256 + 11025 * e8 / 16384 + 43659 * e10 / 65536 + 693693 * e_12 / 1048576;
decimal B1 = 3 * e12 / 8 + 15 * e4 / 32 + 525 * e6 / 1024 + 2205 * e8 / 4096 + 72765 * e10 / 131072 + 297297 * e_12 / 524288;
decimal C1 = 15 * e4 / 256 + 105 * e6 / 1024 + 2205 * e8 / 16384 + 10395 * e10 / 65536 + 1486485 * e_12 / 8388608;
decimal D1 = 35 * e6 / 3072 + 105 * e8 / 4096 + 10395 * e10 / 262144 + 55055 * e_12 / 1048576;
decimal E1 = 315 * e8 / 131072 + 3465 * e10 / 524288 + 99099 * e_12 / 8388608;
decimal F1 = 693 * e10 / 1310720 + 9009 * e_12 / 5242880;
decimal G1 = 1001 * e_12 / 8388608;
// 中央子午线 度转为秒值 如=105*3600
decimal l0 = L0 * 3600; // L0为中央子午线,需要自己设置
// 转为秒值
decimal LL = L * 3600;
// 转为弧度值 b
decimal t_B = B * this.pi / 180;
// 转为秒值 l
decimal t_L = (LL - l0) / p;
decimal L2 = pow(t_L, 2); // t_L * t_L;
decimal L4 = pow(t_L, 4); // L2 * L2;
decimal sinB = sin(t_B);
decimal sinB2 = sinB * sinB;
decimal W = sqrt(1 - e12 * sinB2);
decimal N = a / W;
decimal t = tan(t_B);
decimal t2 = t * t;
decimal t4 = t2 * t2;
decimal cosB = cos(t_B);
decimal cosB2 = cosB * cosB;
decimal cosB4 = cosB2 * cosB2;
decimal y2 = e22 * cosB2; // η2
decimal y4 = y2 * y2;
decimal l_p = t_L; // t_L/p,上面t_L已经除了p值,这里就不再除p值
decimal l2_p2 = L2; // l2/(p*p);
decimal l4_p4 = L4; // l4/(p*p*p*p);
decimal a0 = a * (1 - e12);
// 计算子午弧长公式xx
decimal xx = a0 * (A1 * t_B - B1 * sin(2 * t_B) + C1 * sin(4 * t_B) - D1 * sin(6 * t_B) + E1 * sin(8 * t_B) - F1 * sin(10 * t_B) + G1 * sin(12 * t_B));
// 计度平面坐标值x,y
x = xx + N * t * cosB2 * l2_p2 * (0.5M + (5 - t2 + 9 * y2 + 4 * y4) * cosB2 * l2_p2 / 24 + (61 - 58 * t2 + t4) * cosB4 * l4_p4 / 720);
y = N * cosB * l_p * (1 + (1 - t2 + y2) * cosB2 * l2_p2 / 6 + (5 - 18 * t2 + t4 + 14 * y2 - 58 * y2 * t2) * cosB4 * l4_p4 / 120);
// 转为高斯投影是否为大数投影? 即Zone 35带数(小数投影为CM_105E)
if (IsBigNumberProj == true)
{
y = y + (L0 / (int)Strip) * 1000000M; // L0为中央子午线,Strip为分度带(3或者6)
}
y = y + 500000.0M;
return new GaussPoint(toNum(x), toNum(y));
}
②高斯投影反算:平面坐标(X, Y) ==> 大地坐标/经纬度坐标(L, B)。
B和L的单位为弧度(度分秒)。当L<3.5°时,上式换算经度达0.0001″。要让换算精确度至0.01″,可以简化如下:
公式转换为代码,网上的大都大同小异,这里扒了一段作为代码实现,已经验证过了,转换结果基本正确。
实体代码:
/// <summary>
/// 经纬度实体
/// </summary>
public class Lnglat
{
public Lnglat()
{
}
/// <summary>
/// 经纬度实体
/// </summary>
/// <param name="lng">经度</param>
/// <param name="lat">纬度</param>
public Lnglat(double lng, double lat)
{
this.Lat = lat;
this.Lng = lng;
}
/// <summary>
/// 经度
/// </summary>
public double Lng { get; set; }
/// <summary>
/// 纬度
/// </summary>
public double Lat { get; set; }
}高斯反算代码:
/// <summary>
/// 高斯反算方法 (x,y)=>(B,L)
/// </summary>
/// <param name="x">高斯点X</param>
/// <param name="y">高斯点Y</param>
/// <returns>返回经纬度实体</returns>
public Lnglat GetBLFromXY(decimal x, decimal y)
{
decimal B = 0, L = 0;
// 去掉大数和东移500公里
decimal y1 = y - 500000.0M;
if (IsBigNumberProj == true)
{
y1 = y1 - (L0 / (int)Strip) * 1000000M; // L0为中央子午线,Strip为分度带(3或者6)
}
y = y1;
// 中央子午线转为秒值 如=105*3600
decimal l0 = L0 * 3600; // L0为中央子午线,需要自己设置
// 计算临时值
decimal e4 = pow(e12, 2); // e2 * e2;
decimal e6 = pow(e12, 3); // e4 * e2;
decimal e8 = pow(e12, 4); // e6 * e2;
decimal e10 = pow(e12, 5); // e8 * e2;
decimal e_12 = pow(e12, 6); // e10 * e2;
decimal A1 = 1 + 3 * e12 / 4 + 45 * e4 / 64 + 175 * e6 / 256 + 11025 * e8 / 16384 + 43659 * e10 / 65536 + 693693 * e_12 / 1048576;
decimal B1 = 3 * e12 / 8 + 15 * e4 / 32 + 525 * e6 / 1024 + 2205 * e8 / 4096 + 72765 * e10 / 131072 + 297297 * e_12 / 524288;
decimal C1 = 15 * e4 / 256 + 105 * e6 / 1024 + 2205 * e8 / 16384 + 10395 * e10 / 65536 + 1486485 * e_12 / 8388608;
decimal D1 = 35 * e6 / 3072 + 105 * e8 / 4096 + 10395 * e10 / 262144 + 55055 * e_12 / 1048576;
decimal E1 = 315 * e8 / 131072 + 3465 * e10 / 524288 + 99099 * e_12 / 8388608;
decimal F1 = 693 * e10 / 1310720 + 9009 * e_12 / 5242880;
decimal G1 = 1001 * e_12 / 8388608;
// 求底点纬度值Bf
decimal B0 = x / (a * (1 - e12) * A1);
decimal Bf = 0.0M;
decimal FB = 0.0M;
decimal FB1 = 0.0M;
decimal a0 = a * (1 - e12);
decimal delta = Math.Abs(Bf - B0);
while (delta > 4.8E-11M) // 0.000000000048M
{
Bf = B0;
FB = a0 * (A1 * Bf - B1 * sin(2 * Bf) + C1 * sin(4 * Bf) - D1 * sin(6 * Bf) + E1 * sin(8 * Bf) - F1 * sin(10 * Bf) + G1 * sin(12 * Bf));
FB1 = a0 * (A1 - 2 * B1 * cos(2 * Bf) + 4 * C1 * cos(4 * Bf) - 6 * D1 * cos(6 * Bf) + 8 * E1 * cos(8 * Bf) - 10 * F1 * cos(10 * Bf) + 12 * G1 * cos(12 * Bf));
B0 = Bf + (x - FB) / FB1;
//
delta = Math.Abs(Bf - B0);
}
decimal sinBf = sin(Bf);
decimal sinBf2 = sinBf * sinBf;
decimal W = sqrt(1 - e12 * sinBf2);
decimal W3 = W * W * W;
decimal N = a / W;
decimal t = tan(Bf);
decimal t2 = t * t;
decimal t4 = t2 * t2;
decimal cosBf = cos(Bf);
decimal cosBf2 = cosBf * cosBf;
decimal yy = e22 * cosBf2; // η2
decimal Mf = a0 / W3;
decimal y_N = y / N;
decimal y_N2 = y_N * y_N;
decimal y_N4 = y_N2 * y_N2;
// 计算经伟度值B,L
decimal t_B = Bf * p - (p * t / (2 * Mf) * y * y_N) * (1 - (5 + 3 * t2 + yy - 9 * yy * t2) * y_N2 + (61 + 90 * t2 + 45 * t4) * y_N4 / 360);
decimal t_L = (p / cosBf) * y_N * (1 - (1 + 2 * t2 + yy) * y_N2 / 6 + (5 + 28 * t2 + 24 * t4 + 6 * yy + 8 * yy * t2) * y_N4 / 120);
// 计算经纬度
L = t_L + l0;
// 转为度
B = t_B / 3600;
// 转为度
L = L / 3600;
return new Lnglat(toNum(L), toNum(B));
}*正反算推算过程和实例都在参考资料中,具体可以参考《大地测量学基础》,里面有非常详细的推演过程,但是原理讲解我觉得不是特别明白,有点让人一头雾水,可能是我道行微末的原因。
注意1:正反算方法中的e12,e22等参数,对应的是上面椭球参数。
注意2:正反算方法里的pow、sqrt、tan、toNum等方法,对应的是Math.Pow、Math.Sqrt等C#内置函数的方法,这里只是做了封装。
*自己实现了下七参数和高斯正反算的功能

4.Environment and Configuration
Environment:Windows 7及以上
Language:C#
IDE:Visual Studio 2019
5.Conclusion
高斯正反算原理弄不清楚的,明白个大概就好(不包括大佬),关键是要知道怎么用、用来干嘛的、怎么调整参数等等。
附上所用的参考资料:https://pan.baidu.com/s/1Asw1hYVR42GD9oBI3QdJqw 提取码:5qrc








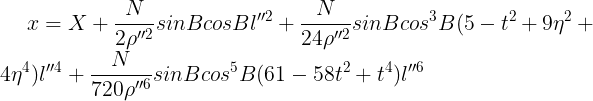
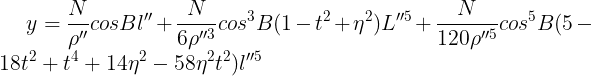
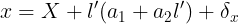
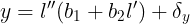

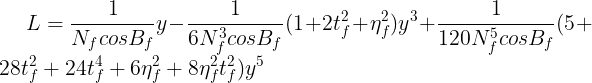

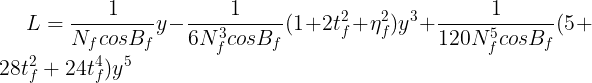

















 6942
6942

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










