学而思/奥数翻杯子问题的解法

翻杯子问题是奥数中的一个经典题型，大致问题就是如下所示：

 

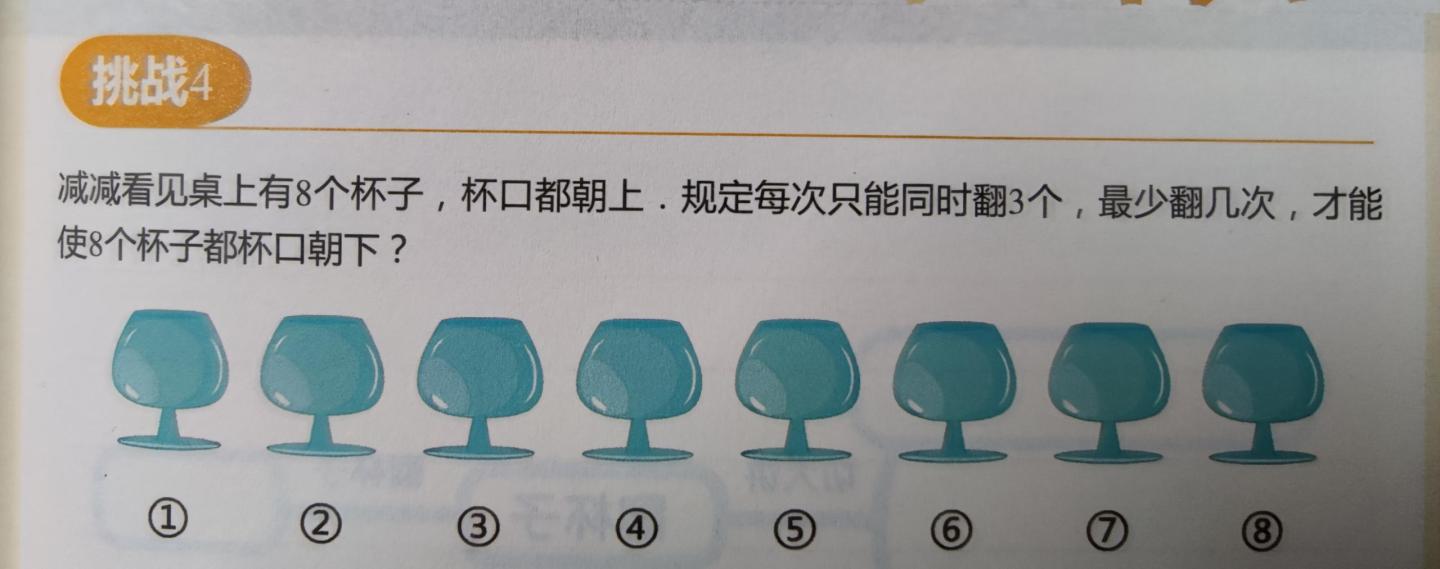
这种题变化很多，其实也是有规律的，如果小朋友实在学不会，可以试试下面的公式

假设杯子的个数是N个，每次翻M个，那么最少全部翻过来的次数是X次，则公式如下：

上来第一步，先判断奇偶性：

一，如果N为奇数，M为偶数，则X是不存在的。为什么呢？一个杯子想要被翻过来，其被翻的次数一定是奇数次，那么N为奇数的情况下，所有杯子总共被翻的次数就是奇数个奇数相加，结果还是个奇数，而奇数是无法整除M这个偶数的，所以这种情况无法完成目标。

二，排除掉第一条，我们来看几种不同的情况：

2.1，N为M的整数倍，这个最简单，X=N/M，这个很好理解吧

2.2，N=M+1，这个第二简单，X=N，就是轮着翻，相当于每次翻一个

2.3，N>2M，也就是每次翻的数量不到总数的一半，这时怎么算呢，也是有公式的，因为我们需要一个杯子被翻奇数倍，所以就从每个杯子翻一次开始算，需要满足一个条件就是：所有杯子总共翻的次数要能够被每次翻的杯子数整除，于是就是先把其中一个杯子从1次变3次，总次数加2，再不行就两个杯子变3次，总次数加4，以此类推，也就是先用N/M，看能否整除，如果不能，就用(N+2)/M，还不行就用(N+4)/M，直到能够整除，而整除之后这个商，就是最终的次数，比如8个杯子每次翻3个，8/3不行，10/3不行，12/3=4可以，所以答案就是4。

2.4，N<2M，也就是每次翻的数量超过总数的一半了，这时又相对简单了，记住就行了：

2.4.1，N与M奇偶性相同，翻3次搞定

2.4.2，N为偶而M为奇，翻4次搞定

至此所有情况都已列举完毕，记住，一定要按照从前往后这个顺序判断，不能用单一方法计算。

可以尝试下1~9个杯子的不同情况，如下表

最后，附送一个思维导图，一图搞定

 

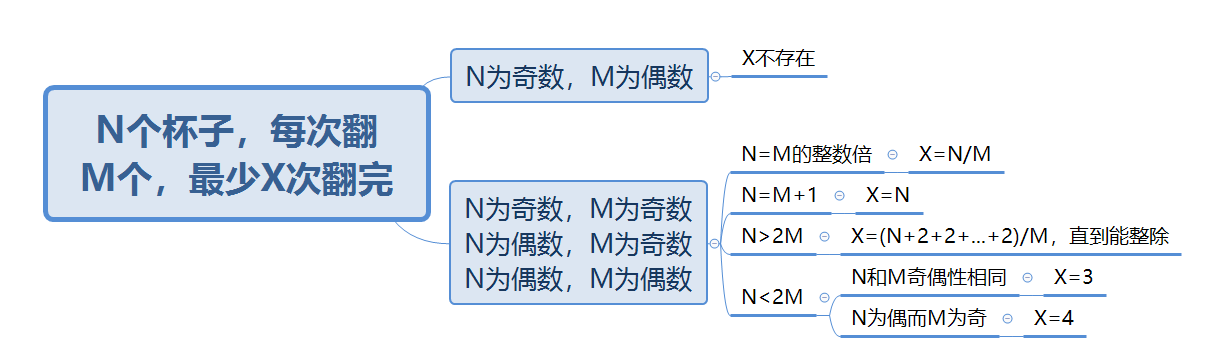
如果小朋友学过编程，也可以用编程的思想来描述这个解法，编程思想非常好的解释了这个过程，即你必须顺序执行这个程序，而不能使用中间的某一个判别条件：

题目：N个杯子，每次翻M个，最少X次翻完，求X

如果：N为奇数 且 M为偶数
        那么：X不存在，程序结束
如果：N=M的整数倍
        那么：X=N/M
如果：N=M+1
        那么：X=N
如果：N>2M
        那么：X=循环执行（N=N+2，N/M，结果为整数）
如果：N<2M
        如果：N和M奇偶性相同
                那么：X=3
        如果：N和M奇偶性不同
                那么：X=4
程序结束