反向传播算法详解-CSDN博客

本文链接：https://blog.csdn.net/weixin_42036865/article/details/94633681

导语

导语

说到神经网络的实现，其实就是调整各个神经元之间的参数（w，b），但是介于各层神经元之间的连接，所以推出反向传播来实现各个参数的调整，接下来，我们看一下如何进行反向传播。

什么是反向传播？

BP算法(即反向传播算法)适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

计算反向传播基本步骤

1.   计算参数维度（方便计算矩阵相乘关系）
2.   梳理前向传播的步骤及维度（更好推导反向传播）
3.   进行反向传播计算（利用链式编程）

传播案例图解析

这是一个简单的神经网络结构图，输入两个维度的数据，最后通过两次sigmoid激活预测二分类结果。

具体步骤

1.计算参数维度

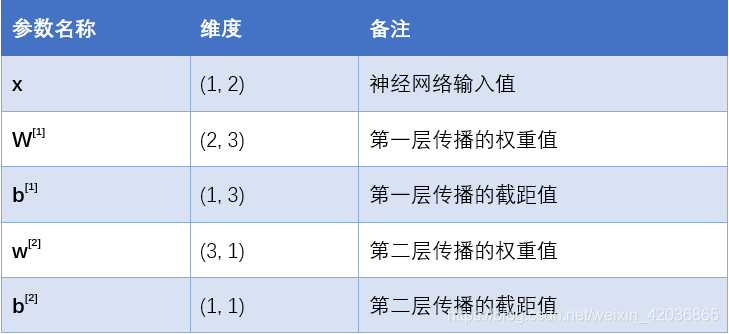
2.前向传播步骤及维度

3.进行反向传播计算

利用反向传播，进行梯度下降，求出dw1,dw2,db1,db2的值，然后使用公式计算

第一步，求da2的偏导数

（这里的da2只是一个符号，不要误会！！！以下符号相同）

$\begin{aligned} da_2&=\frac{\partial{L}}{\partial{a_2}}\\ &=-[\frac{y}{a_2}+\frac{1-y}{1-a_2}\cdot(-1)]\\ &=\frac{1-y}{1-a_2}-\frac{y}{a_2}\\ &=\frac{a_2-a_2y}{a_2(1-a_2)}-\frac{y-a_2y}{a_1(1-a_2)}\\ &=\frac{a_2-y}{a_2(1-a_2)}\\ \end{aligned}$

第二步，求dz2的偏导数（利用链式推导）：

先求 $\frac{\partial{a_2}}{\partial{z_2}}\\$ 的偏导

$\begin{aligned} \frac{\partial{da_2}}{\partial{dz_2}}&=\frac{-e^{-z_2}\cdot(-1)}{(1+e^{-z_2})^2}\\ &=\frac{e^{-z_2}}{(1+e^{-z_2})^2}\\ &=\frac{1+e^{-z_2}-1}{(1+e^{-z_2})^2}\\ &=\frac{1+e^{-z_2}}{(1+e^{-z_2})^2}-\frac{1}{(1+e^{-z_2})^2}\\ &=a_2-{a_2}^2\\ &=a_2(1-a_2) \end{aligned}$

通过上式求 $\frac{\partial{L}}{\partial{dz_2}}$ :

$dz_2=\frac{\partial{L}}{\partial{z_2}} =\frac{\partial{L}}{\partial{a_2}}\cdot\frac{\partial{a_2}}{\partial{z_2}} =\frac{a_2-y}{a_2(1-a_2)}\cdot{a_2(1-a_2)}=a_2-y$