《数据结构》上机实验(第五章)——递归

最新推荐文章于 2022-11-03 07:50:38 发布

—Miss. Z—

最新推荐文章于 2022-11-03 07:50:38 发布

阅读量2.5k

点赞数 2

分类专栏：《数据结构》上机实验文章标签：数据结构模式匹配算法递归 c语言 visual studio

本文链接：https://blog.csdn.net/weixin_42071236/article/details/119771506

版权

《数据结构》上机实验专栏收录该内容

28 篇文章 102 订阅

订阅专栏

1. 已知A[0…n-1]为整数数组，设计一个递归算法求这n个元素的平均值。

A[0…n-1]共有n个元素。
当n=1时，有一个元素，即A[0]。平均值为A[0]；
当n=2时，有两个元素，即A[0]、A[1]。平均值为 $\frac{A[0]×1+A[1]}{2}$ 。
当n=3时，有三个元素，即A[0]、A[1]、A[2]。平均值为 $\frac{\frac{A[0]+A[1]}{2}×2+A[2]}3$ 。

设average[A,n]返回A[0…n-1]共n个元素的平均值，则递归模型如下：
$average(A,n)=\begin{cases} A[0]\;\;\;\;n=1 \\ \frac{averge(A,n-1)×(n-1)+A[n-1]}{n}\;\;\;\;n ≥ 2 \\ \end{cases}$

double average(int A[],int n)
{
	if (n == 1) return A[0];
	else return (average(A,n-1) * (n-1)+A[n-1]) / n;
}

运行结果

在这里插入图片描述

2. 设计一个算法求正整数n的位数。

先将正整数÷10，如果该数在1~9之间，则结束。否则，将该数继续÷10。

设count(n)为正整数n的位数，则递归模型如下：
$count(n)=\begin{cases} 1\;\;\;\;n<10 \\ count(\frac{n}{10})+1\;\;\;\;n ≥ 10 \\ \end{cases}$

int count(int n)
{
	if (n < 10) return 1;
	else return count(n / 10) + 1;
}

运行结果

在这里插入图片描述

3. 上楼可以一步上一阶,也可以一步上两阶，设计一个递归算法，计算共有多少种不同的走法。

设f(n)表示n阶楼梯的不同的走法数，显然f(1) = 1，f(2) = 2(两阶有一步一步走和两步走2种走法)。f(n=1)表示n=1阶楼梯的不不同走法数，f(n=2)表示n=2阶楼梯的不同的走法数，对于n阶楼梯，第1步上一阶有个f(n-1)种走法，第1步上两阶有f(n-2)种走法，则f(n) = f(n-1) + f(n-2)。

设fun(n)为n阶楼梯的走法数，则递归模型如下：
$fun(n)=\begin{cases} 1\;\;\;\;n=1 \\ 2\;\;\;\;n=2 \\ fun(n-1)+fun(n-2)\;\;\;\;n>2 \\ \end{cases}$

int fun(int n)
{
    if (n == 1 || n == 2) return n; 
    else  return fun(n - 1) + fun(n - 2);
}

运行结果

①1 1 1 1 1 ②1 2 1 1
③1 1 2 1 ④1 1 1 2
⑤1 2 2 ⑥2 1 1 1
⑦2 1 2 ⑧2 2 1

4. 设计一个递归算法，利用顺序串的基本运算求串s的逆串。

对于 $s="s_1s_2...s_n"$ 的串，假设" $s_2s_3...s_n$ "已求出其逆串即f(SubStr(s, 2, StrLength(s) -1))，再将s1(为SubStr(s, 1, 1))单个字符构成的串连接到最后即得到s的逆串。

求逆串的递归模型如下：
$f(s)=\begin{cases} f(s) = s \;\;\;\;若s = Φ \\ f(s) = Concat(f(SubStr(s, 2, StrLength(s) - 1)), SubStr(s, 1, 1))\;\;\;\;其他情况 \\ \end{cases}$

SqString invert(SqString s)
{
	SqString  s1, s2;
	if (StrLength(s) > 0)
	{
		s1 = invert(SubStr(s, 2, StrLength(s) - 1));
		s2 = Concat(s1, SubStr(s, 1, 1));
	}
	else StrCopy(s2, s);
	return s2;
}

5. 设计一个递归算法，利用串的基本运算SubStr()判断字符x是否在串s中。

递归模型为：
$Find(s,x)=\begin{cases} 0 \;\;\;\;如果s为空串 \\ 1 \;\;\;\;如果a_1=x \\ Find("a_2...a_n",x) \;\;\;\;其他情况\\ \end{cases}$

bool Find(SqString s, char x)
{
	SqString s1;
	if (s.length == 0) return false;
	else if (s.data[0] == x) return true; //a1=x
	else
	{
		s1 = SubStr(s, 2, s.length - 1); //s1="a2...an"
		return Find(s1, x);
	}
}

6. 设有一个不带表头结点的单链表L，设计两个递归算法，traverse(L)正向输出单链表L的所有结点值，traverseR(L)反向输出单链表L的所有结点值。

void traverse(LinkList L)
{
	if (L == NULL) return;
	printf("%d ", L->data);
	traverse(L->next);
}

void traverseR(LinkList L)
{
	if (L == NULL) return;
	traverseR(L->next);
	printf("%d ", L->data);
}

运行结果

在这里插入图片描述

7. 设有一个不带表头结点的单链表L，设计两个递归算法，del(L,x)删除单链表L中第一个值为x的结点，delall(L,x)删除单链表L中所有值为x的结点。

void del(LinkList &L,ElemType x)
{
	LNode* p;
	if (L == NULL) return;
	if (L->data == x)
	{
		p = L;
		L = L->next;
		free(p);
		return;
	}
	del(L->next, x);
}

void delall(LinkList &L,ElemType x)
{
	LNode* p;
	if (L == NULL) return;
	if (L->data == x)
	{
		p = L;
		L = L->next;
		free(p);
	}
	del(L->next, x);
}

运行结果

直接 $f r e e (p)$ 结点不会造成断链，因为L为引用类型，是直接对原链表进行操作的。

8. 设有一个不带表头结点的单链表L，设计两个递归算法，maxnode(L)返回单链表L中的最大结点值，minnode(L)返回单链表L中的最小结点值。

ElemType maxnode(LinkList L)
{
	int max;
	if (L->next == NULL) return L->data;
	max = maxnode(L->next);
	if (L->data > max) max = L->data;
	return max;
}

ElemType minnode(LinkList L)
{
	int min;
	if (L->next == NULL) return L->data;
	min = minnode(L->next);
	if (L->data < min) min = L->data;
	return min;
}

运行结果

在这里插入图片描述

9. 设有一个不带表头结点的单链表L，设计一个递归算法count(L)求以L为首结点指针的单链表的结点个数。

int count(LinkList L)
{
	if (L == NULL) return 0;
	else	return count(L->next) + 1;
}

运行结果

在这里插入图片描述

10. 用递归方法求单链表中的倒数第k个结点。

LNode* kthNode(LinkList L, int k, int& i)
{
	LNode* p;
	if (L == NULL) return NULL;
	p = kthNode(L->next, k, i);
	i++;
	if (i == k) return L;
	return p;
}

运行结果

在这里插入图片描述

11. 设计一个模式匹配算法，其中模板串t含有通配符’’，它可以和任意子串匹配。对于目标串s，求其中匹配模板t的一个子串的位置(不能出现在的开头和末尾)。

采用BF模式匹配的思路，当s[i]和t[j]比较时，若t[j]为’*’，j++跳过t的当前’*’。取出s中对应’*‘的字符及其之后的所有字符构成的字符串，即Substr(s,i+1,s.length–)，其中i+1是s中对应’*‘字符的字符的逻辑序号。再取出t中’*'字符后面的所有字符构成的字符串，即 Substr(t,j+1,t.length-j)，递归对它们进行匹配，若返回值大于-1，表示匹配成功，返回start。当i或者j超界后结束循环，再判断如果是j超界，返回start，否则返回一1。

int findpat(SqString s, SqString t)
{
	int i = 0, j = 0, k, start;
	while (i < s.length && j < t.length)
	{
		if (t.data[i] == '*')
		{
			j++;
			k = findpat(SubStr(s, i + 1, s.length - 1), SubStr(t, j + 1, t.length - j));
			if (k > -1) return start;
		}
		else if (s.data[i] == t.data[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			start = i;
			j = 0;
		}
	}
	if (j >= t.length) return start;
	else return -1;
}

12. 编写一个递归算法，读入一个字符串(以"."作为结束)，要求打印出它们的倒序字符串。

void reverse()
{
	char ch;
	scanf("%c", &ch);
	if (ch != '.')
	{
		reverse();
		printf("%c", ch);
	}
}

运行结果

在这里插入图片描述

13. 一个人赶着鸭子去每个村庄卖，每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子，问他出发时共赶多少只鸭子？经过每个村子卖出多少只鸭子？

经过了七个村子后还剩2只
设经过了六个村子后还剩x只，则 $x-(\frac{x}{2}+1)=2 \rightarrow$ 即x=(2+1)×2
设经过了五个村子后还剩y只，则 $y-(\frac{y}{2}+1)=x\rightarrow$ 即y=(x+1)×2

设fun(n)表示经过n个村子后还剩下的鸭子数，则递归模型如下：
$fun(n)=\begin{cases} 2\;\;\;\;n=7 \\ (fun(n+1)+1)×2\;\;\;\;其他 \\ \end{cases}$

int fun(int n)
{
	if (n == 7) return 2;
	return (fun(n + 1) + 1) * 2;
}

运行结果

在这里插入图片描述

14. 求解猴子吃桃问题。海滩上有一堆桃子，5只猴子来分。第一只猴子把这堆桃子分成5份，多了一个，这只猴子把多的一个扔入海中，拿走了一份。第2只猴子把剩下的桃子又平均分成5份，又多了一个，它同样把多的一个扔入海中，拿走了一份，第3、第4、第5只猴子都是这样做的，问海滩上原来最少有多少个桃子？

设fun(i)表示第i个猴子分桃子前的桃子总数。显然，第5只猴子分桃子后的桃子总数为m(相当于第6个猴子分桃子前的桃子总数，可以是任何大于等于0的整数)。f(n+1)应该是 $\frac{f(n)-1}{5}$ 的4倍，即 $f(n+1)=4×\frac{f(n)-1}{5}$ ，求出 $f(n)=5×\frac{f(n+1)}{4}+1$ ，而f(n)一定为整数，所以m应该取保证所有 $5×\frac{f(n+1)}{4}$ 整除的最小整数。

对应的递归模型为：
$\begin{cases} fun(6)=m\;\;\;\;第5只猴子分桃子后的桃子总数为m \\ fun(n)=(fun(n+1)+1)*5\;\;\;\;当n>1 \\ \end{cases}$

bool isn(int x, int y) //x整除y时返回true
{
	if (x % y == 0) return true;
	return false;
}

int fun(int n, int m)
{
	if (n == 6) return m;
	else
	{
		if (isn(5 * fun(n + 1, m), 4)) return 5 * fun(n + 1, m) / 4 + 1;
		else return -1; //当m不合适时返回-1
	}
}

int pnumber()
{
	int k;
	int m = 0; //从0开始试探
	while (true)
	{
		k = fun(1, m);
		if (k != -1) break;
		m++;
	}
	return k;
}

运行结果

在这里插入图片描述

15. 有以下递归计算公式：

$\begin{cases} C(n,0)=1\;\;\;\;n≥0 \\ C(n,n)\;\;\;\;n≥0 \\ C(n,m)=C(n-1,m)+C(n-1,m-1)\;\;\;\;n＞m,n≥0,m≥0\\ \end{cases}$
设计一个递归算法和一个非递归算法，求C(n,m)。

int fun1(int n, int m) //递归算法
{
	if (n >= 0 && m == 0 || n >= 0 && m == n) return 1;
	else if (n > m && n >= 0 && m >= 0) return fun1(n - 1, m) + fun1(n - 1, m - 1);
}

int fun2(int n, int m) //非递归算法
{
	int arr[10][10] = { 0 }, i, j;
	for (i = 0; i < n; i++)
	{
		arr[i][0] = 1;
		arr[i][i] = 1;
	}
	for (j = 1; j <= m; j++)
		for (i = j + 1; i <= n; i++)
		{

			arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
		}
	return arr[n][m];
}

运行结果

递归算法是倒着求结果，即C(5,2)=C(4,2)+C(4,1);

其中C(4,2)=C(3,2)+C(3,1)，C(4,1)=C(3,1)+C(3,0);
… …

非递归是正着求结果，即C(0,0)=1,C(1,0)=1,C(1,1)=1;

C(2,0)=1；C(2,1)=C(1,1)+C(1,0)=2；C(2,2)=1

C(3,0)=3；C(3,1)=C(2,1)+C(2,0)=3；… …

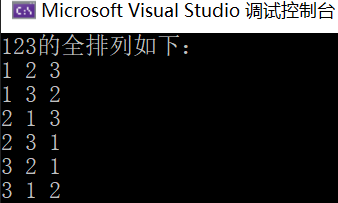
16. 设计一个程序求解全排列问题：输入n个不同的字符，给出它们所有的n个字符的全排列。

void perm(char str[], int k, int n)
{
	int i, t;
	if (k == n - 1) print(str, n);
	else
	{
		for (i = k; i < n; i++)
		{
			t = str[k]; str[k] = str[i]; str[i] = t;
			perm(str, k + 1, n);
			t = str[k]; str[k] = str[i]; str[i] = t;
		}
	}
}

运行结果

在这里插入图片描述

总结

在对单链表设计递归算法时，通常采用不带头结点的单链表。L->next表示的单链表一定是不带头结点的，也就是说“小问题”的单链表是不带头结点的单链表，所以“大问题”(即整个单链表)也应设计成不带头结点的单链表。

—Miss. Z—

关注

2
点赞
踩
37

收藏

觉得还不错? 一键收藏
0
评论
《数据结构》上机实验(第五章)——递归

1. 已知A[0…n-1]为整数数组，设计一个递归算法求这n个元素的平均值。A[0…n-1]共有n个元素。当n=1时，有一个元素，即A[0]。平均值为A[0]；当n=2时，有两个元素，即A[0]、A[1]。平均值为A[0]×1+A[1]2\frac{A[0]×1+A[1]}{2}2A[0]×1+A[1]。当n=3时，有三个元素，即A[0]、A[1]、A[2]。平均值为A[0]+A[1]2×2+A[2]3\frac{\frac{A[0]+A[1]}{2}×2+A[2]}332A[0]+A[1]
复制链接

扫一扫