【HDU2222 Keywords Search】AC自动机 | Trie | fail链 | E

【HDU 2222】Keywords Search

Time Limit: 2000/1000 MS (Java/Others)     Memory Limit: 131072/131072 K (Java/Others) Total Submission(s): 81175    Accepted Submission(s): 28317

Tags：AC自动机 Trie树

题目描述

多组数据。每组数据给定 $N$ 个模式串和 $1$ 个文本串，问有几个模式串在文本串中出现了。

输入

$T$ 组。第一行输入组数 $T$。

对于每组数据，包含若干行，第一行一个正整数 $N$，代表模式串个数。

接下来 $N$ 行每行一个模式串 $P$

接下来一行是文本串 $T$

范围：$N\le 10^4，LEN(P)\le 50，LEN(T)\le 10^6$。

输出

每组输入一个整数，代表有多少个模式串在文本串中出现了。

输入样例

1
5
she
he
say
shr
her
yasherhs

输出样例

3

分析

$AC$ 自动机裸题。（然鹅也有坑点）

首先我们在做初始化和建树的时候有以下两个小优化：

• 采用数组型 Trie树（类似链式前向星）而不是多次动态内存分配（同理在 $BFS$ 时自写 $queue$）。
• （参考于白书 $P216$）BFS 求失配指针时，不妨顺便把失配指针当作不存在的边给补上，以消除不必要的循环（可理解为记忆化）

好，接下来我们再考虑如何写匹配函数。

int match(const char *s)
{
	int cnt = 0;
	int now = ROOT;
	for (const char *p=s; *p; ++p)
	{
		now = t[now].next[*p - 'a'];
		cnt += t[now].cnt;
		t[now].cnt;	// 避免模式串重复计数
	}

	return cnt;
}

这个匹配函数的意思是，在树上跑这个串，遇见打计数标记的结点就计一下数。
是不是很简单呢？然而这样做是有问题的。

（首先说明：问题不是出在没有考虑失配上，因为利用白书上的那个优化后失配指针已经成为了树上实实在在的边了，上面那样写和使用失配指针是等价的。）

那么问题到底出在哪呢？其实也很好想。
考虑这个情况：模式串依次输入：$acm、cm、c$，文本串：$acm$
自动机长这样：（虚线是 $fail$ 指针，双圈是有计数标记的结点。失配指针记忆化的边就懒得画啦）

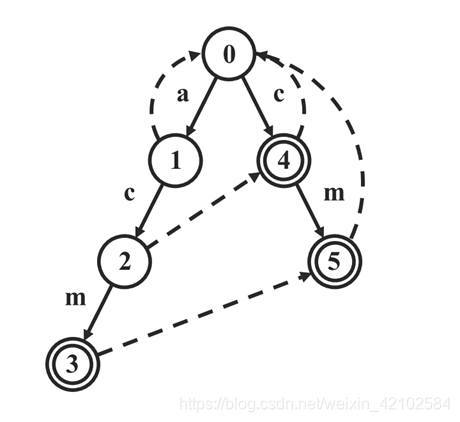
很显然不会出现失配的情况，直接就把 $acm$ 一配到底了。那么如果按照上面函数的流程走，显然函数只会把 $acm$ 对应结点（$3$号）的数给计上，于是 $return1$。然而正确答案显然应该是 $3$。

也就是说，该函数匹配某个串时，会漏掉对它的非前缀的子串的计数。
为什么会漏呢？这是因为 $AC$ 自动机利用了 KMP 算法的思想，也就是不会走 “回头路”。

那么如何才能不漏呢？就需要走一定的 “回头路”。
也就是当走到某个结点时，看一下该点对应的串，有没有什么后缀是某个模式串。
为什么只用看它的所有后缀就行了呢？别忘了这是前缀树，我们只要看了每个前缀的所有后缀，就相当于看了一切子串！
实际上我们也不必看所有后缀。因为有些后缀可能根本不存在于 $Trie$ 上。

所以我们只需要看存在于 $Trie$ 上的、又是当前串的后缀的这些串即可。
这些串在哪呢？都在 以该串对应结点起头的 $fail$ 链上。 $fail$ 指针把它们链在了一起。
为什么呢？因为 $fail$ 链上结点对应的串的特点就是：

• ① 是当前串的后缀（根据 $fail$ 指针定义）
• ② 是某个模式串的前缀（根据 $Trie$ 树，即前缀树的定义）

所以我们只需在每个结点处都遍历一下它起头的 $fail$ 链即可。
当然，为了避免重复遍历，可以利用将 $cnt$ 赋 $-1$ 的技巧来做标记。

再来就是敲代码的时候多脑补一下 Trie树 的结构就行了。是不是很简单呢 然后就可以拿去 $AC$ 啦。

时间复杂度：

• 建 Trie树，$O(N\times LEN(P))$ 的。
• BFS，也是 $O(N\times LEN(P))$ 的。
• 匹配文本串，喜闻乐见 $O(LEN(T))$ 的。
• 遍历 $fail$ 链，最坏最坏均摊 $O(N\times LEN(P))$ 的。
• 总时间复杂度 $O(N\times LEN(P)+LEN(T))$ 。

AC代码

$AC$ 一时爽，$AC$ 自动机一直爽：

#include <cstdio>
#include <cstring>
#define sc(x) {register char _c=getchar(),_v=1;for(x=0;_c<48||_c>57;_c=getchar())if(_c==45)_v=-1;for(;_c>=48&&_c<=57;x=(x<<1)+(x<<3)+_c-48,_c=getchar());x*=_v;}

constexpr int ML(1e6+6);
constexpr int MN(5e5+5);
constexpr int MA(26);

class AC
{
private:

	const int ROOT = 0;
	struct
	{
		int next[MA], fail;
		int cnt;
	} t[MN];	// trie树
	int tot;
	int queue[MN];

public:

	inline void init(void)
	{
		tot = 0;
		memset(t, 0, sizeof(t));
		t[ROOT].fail = -1;
	}

	void insert(const char *s)
	{
		int now = ROOT;
		for (const char *p=s; *p; ++p)
		{
			if (!t[now].next[*p - 'a'])
				t[now].next[*p - 'a'] = ++tot;
			now = t[now].next[*p - 'a'];
		}
		++t[now].cnt;
	}

	void build(void)
	{
		int head = 0, tail = 0;
		for (int i=0; i<MA; ++i)
			if (t[ROOT].next[i])
				queue[tail++] = t[ROOT].next[i], t[t[ROOT].next[i]].fail = 0;

		while (head != tail)
		{
			int fa = queue[head++];
			for (int i=0; i<MA; ++i)
			{
				if (t[fa].next[i])
				{
					queue[tail++] = t[fa].next[i];
					t[t[fa].next[i]].fail = t[t[fa].fail].next[i];
				}
				else
					t[fa].next[i] = t[t[fa].fail].next[i];
			}
		}
	}

	int find(const char *s)
	{
		int cnt = 0, now = ROOT;
		for (const char *p=s; *p; ++p)
		{
			now = t[now].next[*p - 'a'];

			if (~t[now].cnt)
			{
				for (int i=now; i; i=t[i].fail)	// 遍历 fail 链
				{
					if (t[i].cnt == -1)	// 已经访问过了
						break;
					cnt += t[i].cnt;
					t[i].cnt = -1;		// 标记访问
				}
			}
		}

		return cnt;
	}

} ac;



char s[ML];

int main()
{
	int T;
	sc(T)
	while (T--)
	{
		int n;
		sc(n)
		ac.init();
		while (n--)
			scanf("%s", s), ac.insert(s);
		scanf("%s", s);
		ac.build();
		printf("%d\n", ac.find(s));
	}
	
	return 0;
}

听说有人叫自动 $AC$ 机（