图的Dijkstra算法——C/C++

最新推荐文章于 2024-04-17 05:42:59 发布
最新推荐文章于 2024-04-17 05:42:59 发布
阅读量767 收藏 5
点赞数
分类专栏： 数据结构 文章标签： Dijkstra
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_42109012/article/details/94212550
版权

例子：
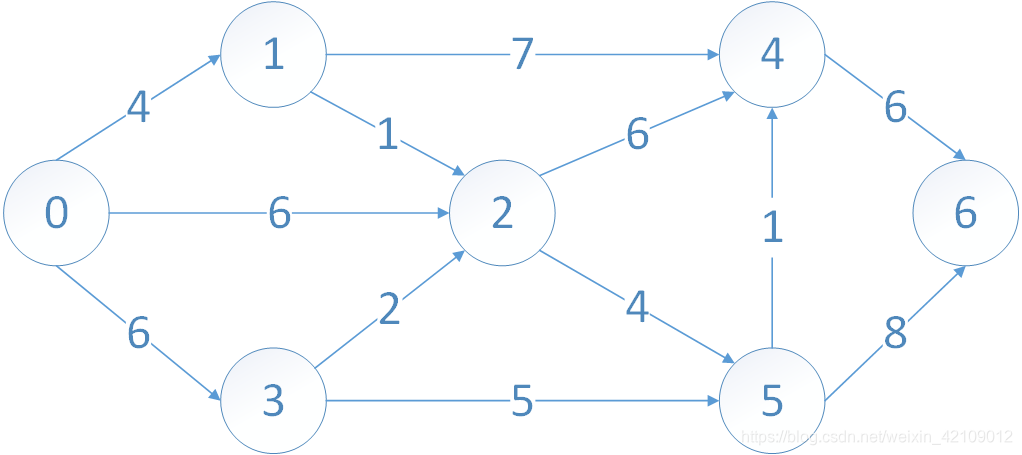
在这里插入图片描述

一、算法原理

1.首先，引入一个辅助向量 dist[]，它的每个分量 dist[] 表示当前所找到的，从起始点（即源点）到其它每个顶点的长度。
例如，dist[6] = 16表示从起始点到顶点3的路径相对最小长度为2。这里强调相对就是说在算法执行过程中 dist[] 的值是在不断逼近最终结果但在过程中不一定就等于长度。

2.dist[] 的初始状态为0：若从 v 到 vj 有边，则 dist[] 为边上的权值，否则置dist[]为∞。
显然，长度为 dist[j] = Min{ dist[] | vi∈V } 的路径就是从 v 出发到顶点 vj 的长度最短的一条路径，路径为（v,vj）。

3.那么，下一条长度次短的是哪一条呢？也就是找到从源点到下一个顶点的最短路径长度所对应的顶点，且这条最短路径长度仅次于从源点到顶点的最短路径长度。
假设该次短路径的终点是 vk，则可想而知，这条路径要么是(v,vk)，或者是(v,vj,vk)。它的长度就是最小的路径长度。

4.一般情况下，假设S为已求得的从源点出发的最短路径长度的顶点的集合，则可证明：下一条次最短路径（设其终点为 x）要么是(v,x)，或者是从源点出发的中间只经过S中的顶点而最后到达顶点的路径。因此，下一条长度次短的的最短路径长度必是 dist[]= Min{ dist[]| vi ∈V-S }，其中 dist[] 要么是(v,vi)上的权值，或者弧(v,vk,vi)上的权值之和。

二、算法思想

1、 初始时令 S={V0},U=V-S={其余顶点}，T中顶点对应的距离值
若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值
若不存在<V0,Vi>，d(V0,Vi)为∞
2.、从T中选取一个与S中顶点有关联边且权值最小的顶点W，加入到S中
3.、对其余T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值缩短，则修改此距离值
重复上述步骤2、3，直到S中包含所有顶点，即W=Vi为止
在这里插入图片描述

三、算法实现

1、Dijkstra算法

void Dijkstra(MatGraph LG, int v) {
	int dist[MAXV];									//存储权值
	int path[MAXV];									//是否有路径
	int S[MAXV];									//S[i]==0表示顶点 i 在S中, S[i]==1 表示 顶点 i 在 U 中
	int MinDis;										//最小的权值
	int u = 0;										//记录最短路径的顶点
	int i, j;
	for (i = 0; i < LG.n; i++) {
		dist[i] = LG.adjMat[v][i];					//距离初始化
		S[i] = 0;									//S[] 初始化
		if (LG.adjMat[v][i] < 32767) {				//路径初始化
			path[i] = v;							//顶点 v 到顶点 i 有边时，置顶点 i 的前一个顶点为 v
		}
		else {
			path[i] = -1;							//顶点 v 到顶点 i 无边时，置顶点 i 的前一个顶点为 -1
		}
	}
	S[v] = 1;										//源点编号 v 放入 S
	path[v] = 0;									
	for (i = 0; i < LG.n - 1; i++) {				//循环求 v 到所有顶点的最短路径
		MinDis = INF;								//置最大长度初值
		for (j = 0; j < LG.n; j++) {
			if (S[j] == 0 && dist[j] < MinDis) {	//选取不在 S 中（即 U 中）且就有路径长度的顶点 u
				u = j;
				MinDis = dist[j];					//得到顶点、路径长度
			}
		}
		S[u] = 1;									//顶点 u 加入 S
		for (j = 0; j < LG.n; j++) {				//修改最短路径
			if (S[j] == 0) {
				if (LG.adjMat[u][j] < INF && dist[u] + LG.adjMat[u][j] < dist[j]) {
					dist[j] = dist[u] + LG.adjMat[u][j];
					path[j] = u;
				}
			}
		}
	}
	displayPath(LG, dist, path, S, v);				//输出最短路径
}

2、输出单源最短路径

void displayPath(MatGraph LG, int dist[], int path[], int S[], int v) {
	int i, j, k;
	int aPath[MAXV];								//存放一条最短路径（逆向）
	int d;											//顶点个数
	for (i = 0; i < LG.n; i++) {					//循环输出从顶点 v 到 i 的路径
		if (S[i] == 1 && i != v) {
			printf("从顶点 %d 到顶点 %d 的路径长度为：%d\t 路径为:", v, i, dist[i]);
			d = 0;
			aPath[d] = i;							//添加路径上的终点
			k = path[i];
			if (k == -1) {							//没有路径
				printf("无路径\n");
			}
			else {									//存在路径就输出
				while (k != v) {
					d++;
					aPath[d] = k;
					k = path[k];
				}
				d++;
				aPath[d] = v;						//添加路径上的起点
				printf("%d ", aPath[d]);			//输出起点
				for (j = d - 1; j >= 0; j--) {		//输出其他顶点
					printf("%d ", aPath[j]);
				}
				printf("\n");
			}
		}
	}
}

四、整体框架

#include<stdio.h>
#include<malloc.h>

#define MAXV 7					//最大顶点个数 
#define INF 32767				//定义 ∞
//∞ == 32767 ,int 型的最大范围（2位）= 2^(2*8-1)，TC告诉我们int占用2个字节，而VC和LGCC告诉我们int占用4个字节
//图：Graph
//顶点：Vertex
//邻接：Adjacency
//矩阵：Matrix
//表：List
//边：Edge 

typedef struct vertex {
	int number;					//顶点的编号 	
}VertexType; 					//别名，顶点的类型 

typedef struct matrix {
	int n;						//顶点个数
	int e;						//边数 
	int adjMat[MAXV][MAXV];		//邻接矩阵数组			
	VertexType ver[MAXV];		//存放顶点信息 
}MatGraph;						//别名，完整的图邻接矩阵类型

typedef struct eNode {
	int adjVer;					//该边的邻接点编号 
	int weiLGht;				//该边的的信息，如权值 
	struct eNode* nextEdLGe;	//指向下一条边的指针 
}EdgeNode; 						//别名，边结点的类型 

typedef struct vNode {
	EdgeNode* firstEdLGe;		//指向第一个边结点 
}VNode; 						//别名，邻接表的头结点类型 

typedef struct list {
	int n;						//顶点个数
	int e;						//边数
	VNode adjList[MAXV];		//邻接表的头结点数组 
}ListGraph;						//别名，完整的图邻接表类型 

//创建图的邻接表 
void createAdjListGraph(ListGraph* &LG, int A[MAXV][MAXV], int n, int e) {
	int i, j;
	EdgeNode* p;
	LG = (ListGraph*)malloc(sizeof(ListGraph));
	for (i = 0; i < n; i++) {
		LG->adjList[i].firstEdLGe = NULL;						//给邻接表中所有头结点指针域置初值 
	}
	for (i = 0; i < n; i++) {									//检查邻接矩阵中的每个元素 
		for (j = n - 1; j >= 0; j--) {
			if (A[i][j] != 0) {									//存在一条边 
				p = (EdgeNode*)malloc(sizeof(EdgeNode));		//申请一个结点内存
				p->adjVer = j;									//存放邻接点 
				p->weiLGht = A[i][j];							//存放权值
				p->nextEdLGe = NULL;

				p->nextEdLGe = LG->adjList[i].firstEdLGe;		//头插法 
				LG->adjList[i].firstEdLGe = p;
			}
		}
	}
	LG->n = n;
	LG->e = e;
}

//输出邻接表 
void displayAdjList(ListGraph* LG) {
	int i;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		p = LG->adjList[i].firstEdLGe;
		printf("%d:", i);
		while (p != NULL) {
			if (p->weiLGht != 32767) {
				printf("%2d[%d]->", p->adjVer, p->weiLGht);
			}
			p = p->nextEdLGe;
		}
		printf(" NULL\n");
	}
}

//输出邻接矩阵
void displayAdjMat(MatGraph LG) {
	int i, j;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			if (LG.adjMat[i][j] == 0) {
				printf("%4s", "0");
			}
			else if (LG.adjMat[i][j] == 32767) {
				printf("%4s", "∞");
			}
			else {
				printf("%4d", LG.adjMat[i][j]);
			}
		}
		printf("\n");
	}
}

//邻接表转换为邻接矩阵
void ListToMat(ListGraph* LG, MatGraph& MG) {
	int i, j;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			MG.adjMat[i][j] = 0;
		}
	}
	for (i = 0; i < LG->n; i++) {
		p = LG->adjList[i].firstEdLGe;
		while (p != NULL) {
			MG.adjMat[i][p->adjVer] = p->weiLGht;
			p = p->nextEdLGe;
		}
	}
	MG.n = LG->n;
	MG.e = LG->e;
}

//输出单源最短路径
void displayPath(MatGraph LG, int dist[], int path[], int S[], int v) {
	int i, j, k;
	int aPath[MAXV];								//存放一条最短路径（逆向）
	int d;											//顶点个数
	for (i = 0; i < LG.n; i++) {					//循环输出从顶点 v 到 i 的路径
		if (S[i] == 1 && i != v) {
			printf("从顶点 %d 到顶点 %d 的路径长度为：%d\t 路径为:", v, i, dist[i]);
			d = 0;
			aPath[d] = i;							//添加路径上的终点
			k = path[i];
			if (k == -1) {							//没有路径
				printf("无路径\n");
			}
			else {									//存在路径就输出
				while (k != v) {
					d++;
					aPath[d] = k;
					k = path[k];
				}
				d++;
				aPath[d] = v;						//添加路径上的起点
				printf("%d ", aPath[d]);			//输出起点
				for (j = d - 1; j >= 0; j--) {		//输出其他顶点
					printf("%d ", aPath[j]);
				}
				printf("\n");
			}
		}
	}
}

//Dijkstra算法
void Dijkstra(MatGraph LG, int v) {
	int dist[MAXV];									//存储权值
	int path[MAXV];									//是否有路径
	int S[MAXV];									//S[i]==0表示顶点 i 在S中, S[i]==1 表示 顶点 i 在 U 中
	int MinDis;										//最小的权值
	int u = 0;										//记录最短路径的顶点
	int i, j;
	for (i = 0; i < LG.n; i++) {
		dist[i] = LG.adjMat[v][i];					//距离初始化
		S[i] = 0;									//S[] 初始化
		if (LG.adjMat[v][i] < 32767) {				//路径初始化
			path[i] = v;							//顶点 v 到顶点 i 有边时，置顶点 i 的前一个顶点为 v
		}
		else {
			path[i] = -1;							//顶点 v 到顶点 i 无边时，置顶点 i 的前一个顶点为 -1
		}
	}
	S[v] = 1;										//源点编号 v 放入 S
	path[v] = 0;									
	for (i = 0; i < LG.n - 1; i++) {				//循环求 v 到所有顶点的最短路径
		MinDis = INF;								//置最大长度初值
		for (j = 0; j < LG.n; j++) {
			if (S[j] == 0 && dist[j] < MinDis) {	//选取不在 S 中（即 U 中）且就有路径长度的顶点 u
				u = j;
				MinDis = dist[j];					//得到顶点、路径长度
			}
		}
		S[u] = 1;									//顶点 u 加入 S
		for (j = 0; j < LG.n; j++) {				//修改最短路径
			if (S[j] == 0) {
				if (LG.adjMat[u][j] < INF && dist[u] + LG.adjMat[u][j] < dist[j]) {
					dist[j] = dist[u] + LG.adjMat[u][j];
					path[j] = u;
				}
			}
		}
	}
	displayPath(LG, dist, path, S, v);				//输出最短路径
}

int main() {
	ListGraph* LG;
	MatGraph MG;
	int array[MAXV][MAXV] = {
		{  0,  4,  6,  6,INF,INF,INF},
		{INF,  0,  1,INF,  7,INF,INF},
		{INF,INF,  0,INF,  6,  4,INF},
		{INF,INF,  2,  0,INF,  5,INF},
		{INF,INF,INF,INF,  0,INF,  6},
		{INF,INF,INF,INF,  1,  0,  8},
		{INF,INF,INF,INF,INF,INF,  0}
	};

	int e = 12;
	createAdjListGraph(LG, array, MAXV, e);
	displayAdjList(LG);
	printf("\n");

	ListToMat(LG, MG);
	displayAdjMat(MG);
	printf("\n");

	Dijkstra(MG, 0);
	printf("\n");

	return 0;
}

五、结果展示

在这里插入图片描述

有人_295
关注
  • 0
    点赞
  • 踩
  • 5
    收藏
    觉得还不错? 一键收藏
  • 6
    评论
专栏目录
C++标准库中的随机数生成
略游
11-20 3222
C++标准库中的随机数生成 一、伪随机与真随机 数字计算机的结果可以说是固定的、必然的。都是根据现有数据的状态得出接下来的状态。除非硬件损坏，计算机不会产生真正的随机和无法预料的事。在生活中随手抛一个硬币也受到出手动作、状态，以及风速等环境影响。一只蟑螂的运动路线也可能不是随机的。但是在隔绝的环境中一个分子的运动方向可以说是随机的。在量子力学中的测不准原理和波函数坍缩，都说明随机是一个概率，这...
图的最短路径（Dijkstra方法和Floyed方法）
qq_43628835的博客
12-02 424
什么是最短路径？ 1、在非网图中，两顶点之间经过顶点最少的路径，就是最短路径。 2、在网图中，两点之间经过的权值之和最小的路经。 最短路径问题的解决方法 Dijkstra方法（单源点到其他顶点的最短路径） Floyed方法 （任意两点之间的最短路径） 1.Dijkstra方法 算法思想： 1.设置一个集合S存放已经找到最短路径的顶点，初始值为单源点（起始点）。 2.以后每求得一条最短路径v, …...
c++实现迪杰斯特拉算法_dijkstra算法c++代码，2024年最新2024金九银十面试季
最新发布
m0_74918915的博客
04-17 321
需要注意的是，迪杰斯特拉算法只适用于边权重为非负数的情况。如果存在负权边，则需要使用其他算法，例如贝尔曼-福德算法（Bellman-Ford algorithm）或A*算法。迪杰斯特拉算法的时间复杂度为O(|V|^2)，其中|V|为节点数。如果使用堆优化的实现方式，时间复杂度可以降至O(|E|+|V|log|V|)，其中|E|为边数。
ACM模板--邻接表 无向图 Prim Kruskal Dijkstra
xyjikl
04-12 1098
/** * C++: Dijkstra算法获取最短路径(邻接表) * * @author judyge * @date 2014/04/24 */ #include #include #include using namespace std; // 示例类：边的结构体(用来演示) class EData { public: char start; //
Dijkstra算法总结(C/C++)
psudd的博客
10-28 4718
Dijkstra算法：原理分析+代码总结
【一】图算法之Dijkstra算法及C++实现
Allen_Duke的博客
04-13 2941
0. 前言 由于之前一个比赛用到了路径规划，于是就学习了一些图论中路径规划的算法，所以将自己的学习后的代码记录下来以作备忘。但也是只学了图搜索这类的方法，基于采样的RRT等其他方法个人认为不适合我的应用场景，所以也没有了解。 1. Dijkstra算法 单源最短路径问题：给定一个图G=(V，E)G=(V，E)G=(V，E)，求源结点s∈Vs∈Vs∈V到图中每个结点v∈Vv∈Vv∈V的最短路径。 Dijkstra算法就适用于解决带权重的有向图（或无向图）上的单源最短路径问题，同时算法要求图中所有边的权重非负。
Dijkstra.rar_数值算法/人工智能_Visual_C++_
08-12
总之，这个"Dijkstra.rar"文件提供了一个用Visual C++实现的Dijkstra算法示例，可以作为学习和研究的工具，同时对于理解图算法、C++编程以及在人工智能场景中应用算法具有一定的参考价值。通过阅读源代码和运行程序...
shortest.rar_数据结构_C/C++_
08-12
描述提到的“求出一个图中每对结点之间的最短路径”是图论中的经典问题，通常用Dijkstra算法或Floyd-Warshall算法来解决。 1. **数据结构**：在处理图问题时，我们通常会用到两种主要的数据结构——**邻接矩阵**和*...
danyuanzuiduan.rar_数据结构_C/C++_
08-11
- 优先队列：在C++中，可以使用STL中的`<queue>`和`<priority_queue>`来实现Dijkstra算法中的优先队列。 通过分析这个压缩包中的"单源最短路径"程序，我们可以深入理解这两种算法的工作原理，以及它们在实际问题中...
数据结构与算法——面向对象C++设计模式
04-29
例如，动态规划和贪心策略可用于解决最优化问题，图算法如Dijkstra算法和Floyd算法可求解最短路径问题。 在C++中，面向对象编程（OOP）引入了类和对象的概念，使得代码更加模块化和易于管理。类是数据和操作这些...
最短路径算法——Dijkstra算法
03-20
代码实现方面，Dijkstra算法可以使用C++语言实现，如下所示： ```cpp void DijkstraPath(MGraph g,int *dist,int *path,int v0) { int i,j,k; bool *visited=(bool *)malloc(sizeof(bool)*g.n); for(i=0;i;i++)...
（迪杰斯特拉）Dijkstra算法详细讲解（转载）
ACM-ICPC 现役(铜牌) Codeforces Rating: 2172
10-02 3256
迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止 基本思想 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。 初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路
C++ 最短路径之Dijkstra算法
struct_GS的博客
09-08 1713
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。 Dijkstra算法 只能用于计算单源最短路，而且无法处理负权边。 时间复杂度：O() 【代码实现】 //假设有n个点，m条边，求1~n...
Dijkstra算法（c++版）
热门推荐
一串代码的博客
10-21 3万+
迪杰斯特拉算法 最短路径（DP的应用） 单源最短路径，不允许出现负环 核心思想：更新估算距离 时间复杂度与采用的数据结构有关 Array O(v2v^2v2) Binary heap O((V+E)lgV(V+E)lgV(V+E)lgV) Fibonacci heap O(E+VlgVE+VlgVE+VlgV) δ(u,v)≤δ(u,x)+δ(x,v)\delta(u, v) \leq \delt...
matlab dist函数  …
Coding home - 漂流瓶jz
03-14 1万+
dist(A,B)计算A中每个行向量与B中每个列向量之间欧氏距离，A的行向量维数必须等于B的列向量维数 a=[1,2,3],b=[-1,5,6],c=[1,0,1]求a,b,c欧氏距离 dist(a,b')=4.6904, dist(a,c')= 2.8284 dist(c,b')= 7.3485 mandist(A,B)计算A中每个行向量与B中每个列向量之间绝对距离，A的行向量维数必须等
在一些开源框架中，dist文件夹是什么意思
weixin_30682415的博客
05-22 3374
全称是distribution。 distribution英 [dɪstrɪ'bjuːʃ(ə)n]美 ['dɪstrə'bjʊʃən]: 发行版 n. 分布；分配 在某些框架中，因为开发和发布是的内容或者代码形式是不一样的（比如利用Grunt压缩等等)， 这时候就需要一个存放最终发布版本的代码，这就是dist文件夹的用处。 是最终放到服务器上的发布版本。如果是放到开源去，一...
最短路Dijstra算法（复杂节点，优先队列，C++）
Comet的博客
04-11 773
最短路径算法在众多领域都有广泛应用，众多网络流问题都基于或部分基于最短路问题。一种经典的有效解决最短路问题的算法——dijkstra 算法已经得到广泛应用。dijkstra算法是一种label setting算法，适用于一对多，即某一点到其他各点的最短路。通常情况下的最短路算法依赖于邻接矩阵，用以描述网络的拓扑结构。然而在多数情况下，网络中点包含了多个特征，如位置，前后节点等。本文用结构体（类也可以）来表示网络中的节点，用C++语言实现dijkstra算法。
c++实现迪杰斯特拉算法
谁谁谁的的的博客
10-24 887
需要注意的是，迪杰斯特拉算法只适用于边权重为非负数的情况。迪杰斯特拉算法的时间复杂度为O(|V|^2)，其中|V|为节点数。如果使用堆优化的实现方式，时间复杂度可以降至O(|E|+|V|log|V|)，其中|E|为边数。更新距离：对于与当前节点相邻的节点，计算从起点到这些节点的距离，并更新它们的距离值。如果新的距离值比原来的距离值更小，则更新距离值。初始化：将起点的距离设置为0，将其他节点的距离设置为无穷大。选择节点：从未访问的节点中选择距离起点最近的节点，将其标记为已访问状态。
武汉地铁站点最短路径搜索的实现（一）——Dijkstra算法（C++ coding）
06-13
好的，以下是基于 Dijkstra 算法实现武汉地铁站点最短路径搜索的 C++ 代码： ```cpp #include <iostream> #include <vector> #include <queue> #include <climits> using namespace std; const int MAXN = 100; // 最大站点数 const int INF = INT_MAX; // 无穷大 vector<pair<int, int>> adj[MAXN]; // 邻接表存图 int dist[MAXN]; // 距离数组 bool vis[MAXN]; // 访问标记数组 // Dijkstra 算法实现 void dijkstra(int s) { dist[s] = 0; // 初始距离为0 priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; pq.push(make_pair(dist[s], s)); while (!pq.empty()) { int u = pq.top().second; pq.pop(); if (vis[u]) continue; // 已经访问过了 vis[u] = true; for (pair<int, int> edge : adj[u]) { int v = edge.first; int w = edge.second; if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; // 更新距离 pq.push(make_pair(dist[v], v)); } } } } int main() { int n, m; cin >> n >> m; // 输入站点数和边数 for (int i = 0; i < m; i++) { int u, v, w; cin >> u >> v >> w; // 输入边的起点、终点、权值 adj[u].push_back(make_pair(v, w)); adj[v].push_back(make_pair(u, w)); // 无向图 } int s, t; cin >> s >> t; // 输入起点和终点 fill(dist, dist + n, INF); // 初始化距离数组 dijkstra(s); // Dijkstra 算法求最短路径 cout << dist[t] << endl; // 输出起点到终点的最短距离 return 0; } ``` 在代码中，我们使用邻接表存储图，并使用了 STL 中的优先队列来实现 Dijkstra 算法。同时，我们也注意到 Dijkstra 算法适用于边权值非负的图，因此在实现中需要对边权值的范围做出限制。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 6
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值